自动搬运

查看原文

来自洛谷，原作者为

	xiazha **

搬运于2025-08-24 23:09:36，当前版本为作者最后更新于2025-02-10 12:06:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

dp，通过简单观察，发现考虑第 $i$ 列统计方案数时，只需知道如图画的那几条线就行了。

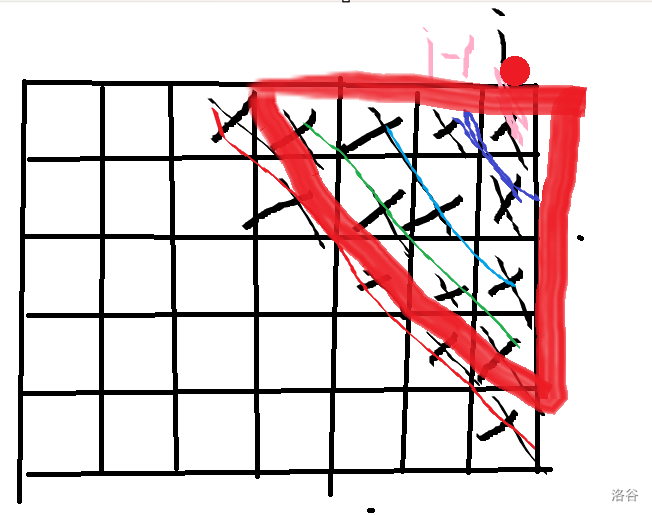
并且这样转移是方便的，对于第 $i$ 列，我们只需记录红颜色方框内的状态并且在转移至 $i+1$ 时状压枚举 $i+1$ 那一列就行了，因此我们可以直接设出一个 $k$ 维 dp，由于定义太长，不做阐述，这个时候你可能想法是直接分 $k=1,2,\cdots,7$ 这几种情况写代码，但是麻烦了，你可以就设一个 $7$ 维 dp 数组，转移时保持后 $\min(6-k,0)$ 维是 $0$ 就行了，具体实现见代码。

时间复杂度 $O(nk 2^kk!)$。（目前为最优解 rk1）

#include<bits/stdc++.h>
using namespace std;
#define mod 1000000007
int n,k,a[202],dp[202][7][6][5][4][3][2],ans;
signed main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>a[i];
	dp[0][0][0][0][0][0][0]=1;
	for(int i=1;i<=n;i++)
		for(int j1=0;j1<=min(6,a[i])*(k>=7);j1++)
			for(int j2=0;j2<=min(5,a[i]-j1)*(k>=6);j2++)
				for(int j3=0;j3<=min(4,a[i]-j1-j2)*(k>=5);j3++)
					for(int j4=0;j4<=min(3,a[i]-j1-j2-j3)*(k>=4);j4++)
						for(int j5=0;j5<=min(2,a[i]-j1-j2-j3-j4)*(k>=3);j5++)
							for(int j6=0;j6<=min(1,a[i]-j1-j2-j3-j4-j5)*(k>=2);j6++)
							{
								for(int s=0;s<(1<<k);s++)
								{
									int f=__builtin_popcount(s);
									if(f+j1+j2+j3+j4+j5+j6!=a[i]) continue;
									int p1=j2+((s&(1<<5))!=0);p1*=(k>=7);
									int p2=j3+((s&(1<<4))!=0);p2*=(k>=6);
									int p3=j4+((s&(1<<3))!=0);p3*=(k>=5);
									int p4=j5+((s&(1<<2))!=0);p4*=(k>=4);
									int p5=j6+((s&(1<<1))!=0);p5*=(k>=3);
									int p6=((s&(1<<0))!=0);p6*=(k>=2);
									dp[i][p1][p2][p3][p4][p5][p6]=(dp[i][p1][p2][p3][p4][p5][p6]+dp[i-1][j1][j2][j3][j4][j5][j6])%mod;
									if(i==n) ans=(ans+dp[i-1][j1][j2][j3][j4][j5][j6])%mod;
								}
							}
	cout<<ans;
	return 0;
}