自动搬运

查看原文

来自洛谷，原作者为

	noip 对你说再见

搬运于2025-08-24 23:09:32，当前版本为作者最后更新于2025-04-15 02:10:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

TEST_189题解

由于本题洛谷上只上传了最大的点，所以期望得分没有意义。

算法 1

每次暴力模拟，总时间复杂度 $O(nm)$，空间复杂度 $O(n)$。

期望得分 5 分。

算法 1.5

考虑对暴力算法进行极限卡常，但是本题操作本质串行，无法使用指令集优化。

这里介绍一种对指令集的通用攻击手段：计算连续访问数组的 L1 缓存缺失量。

强制在线会导致遍历数组时发生大量的 L1 缓存缺失。

为了卡常到极限，利用取模生效次数很少的性质，可以将 $a$ 数组和 $l$ 数组预处理的时候进行合并，这样对于每个位置，只会进行 3​ 次 ​8​ 字节的数组访存。

评测机的 CPU 的 L1 缓存行大小为 32B 的数据缓存和 32B 的指令缓存，每个核心的 L1 缓存总大小为 32KB 的数据缓存和 32KB 的指令缓存。L1 缓存命中时需要约 $4\sim5$ 时钟周期，缺失时需要约 $12\sim14$ 时钟周期。（这段是问 deepseek 的，该数据大致复合正常 CPU 的表现）

如果暴力算法可以通过，则 1s 处理遍历数组时发生的 L1 缓存缺失次数为 $10^5\times 5\times10^5\times 3\times 8/32/10=3.75\times10^9$，由于 CPU 的频率是固定的，所以对时钟周期进行计算可以发现该数据远远超过 CPU 访存极限。

不过对于数据范围较小的测试点，有优化后的暴力算法获得了非平凡的分数。

期望得分 5~15 分。

算法 2

针对 $d_i=0$ 的情况，观察发现取模最多进行 $O(\log v)$ 次，因为每次取模都会导致 $v$ 减半。

考虑每次使用数据结构高效找到接下来第一次该数会发生取模的位置，等价于给定 $x,v$，求 $x$ 后面最近的一个区间，使得区间包含了 $v$。

这个问题可以倒着从后往前维护持久化值域线段树，维护每个值最近被覆盖的时刻，每次加入一个区间的时候做区间染色。

于是对每个位置 $i$，我们有一个持久化值域线段树，支持给定 $v$，查询从 $i$ 开始 $v$ 第一次被覆盖到的时刻。

总时间复杂度 $O(n\log v+m\log^2v)$，空间复杂度 $O(n\log v)$。

期望得分 15 分。

算法 3

如果所有询问的 $R$ 都等于 $n$，有一种持久化平衡树做法。

先考虑简化的，没有 $l_i,r_i$ 限制，并且 $d_i=0$ 的问题。

倒着维护每个后缀的函数复合结果，$f[i][j]$ 表示从 $i$ 开始，初始是 $j$，经过函数复合后到 $n$ 位置的值是多少。

初始是 $f[n][i]=i$ 的恒等映射，使用所谓的 “整体DP” 的思路，还是从后往前倒着维护，每次在原函数复合结果 $f[i+1]$ 前加一个新的函数复合得到 $f[i]$ 时做一个区间复制。注意到这里需要将一个区间变成另一个区间复制多次，这个可以用倍增合并的方法实现单次 $O(\log v)$。

特别需要注意的是，对于持久化 treap 来说，区间复制 $k$ 次的倍增合并是 $O(\log^2v)$ 的，而对于其他拥有更加优秀性质的平衡树（如 WBLT，AVLT），该操作是 $O(\log v)$ 的。

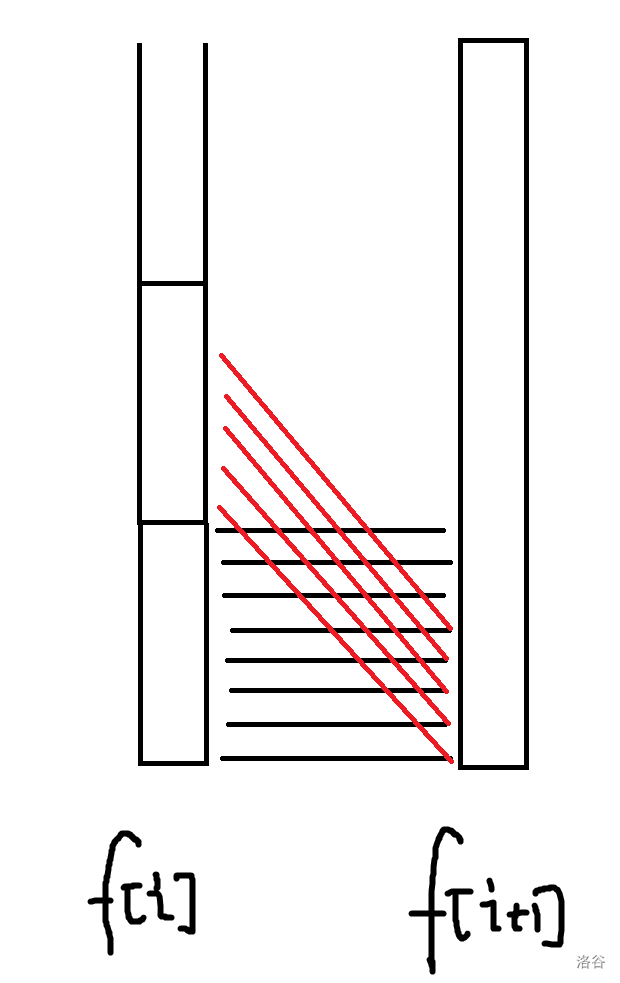
这样可以 $O(n\log v)$ 预处理出每个后缀的持久化平衡树，支持每次 $O(\log v)$ 查询给定 $x$ 和 $l$，求 $x$ 经过 $[l,n]$ 区间函数复合后的结果。

再考虑如果有 $l_i,r_i$ 的限制，并且 $d_i\neq 0$ 该怎么办。可以发现持久化平衡树功能非常强大，区间的限制可以通过每次对 $f[i]$ 只修改其 $[l_i,r_i]$ 部分，其他部分保持不变来实现。$d_i\neq 0$ 可以通过每次对 DP 数组做一个区间平移操作实现，可以用持久化平衡树的操作简单实现。

针对 $R=n$ 的情况，总时间复杂度 $O(n\log v+m\log v)$，空间复杂度 $O(n\log v)$。

期望得分 35 分。

算法 4

回顾算法 2，持久化值域线段树功能受限无法进行区间平移和复制操作，考虑将其换成持久化平衡树来支持更强的操作。

于是倒着从后往前维护持久化平衡树，维护每个点最近被覆盖的时刻，每次的操作有区间染色，区间复制，分裂合并等，都是持久化平衡树支持的操作。

对每次查询，使用预处理好的数据结构每次 $O(\log v)$ 找到最近一次取模的位置，需要取模 $O(\log v)$ 次。

总时间复杂度 $O(n\log v+m\log^2v)$，空间复杂度 $O(n\log v)$。

期望得分 55~75 分。

算法 5

我们发现对于 $R=n$ 我们可以每次 $O(\log v)$ 查询出答案，所以可以对序列分治建立线段树，对线段树的每一层，问题变成 $L=1,R=n$ 的子问题。

每次查询需要按顺序找到 $[L,R]$ 区间的 $O(\log n)$ 个线段树结点，将 $v$ 依次代入得到经过区间函数复合后的结果。

这个方法可以顶层分块，底层分块，将线段树变成多叉线段树来极大地减少常数。

顶层分块：可以发现线段树的根结点的没有用的，只有 $L=1,R=n$ 的查询才会用，所以可以不建立。继续分析可以发现线段树的最上面几层如果拆掉后，会减少预处理复杂度，少量增加查询复杂度。

底层分块：可以发现线段树的叶子结点是没有用的，如果建立的持久化平衡树，则每次查询是 $O(\log v)$ 的，还不如暴力。于是可以底层区间很小时直接暴力计算答案。

多叉线段树：可以发现线段树加上底层分块和顶层分块后二叉就不优了，于是将线段树改为多叉的。

利用右儿子：可以发现线段树结点可以直接从其右儿子处继承过来持久化平衡树，然后只需要将左儿子的部分插入即可。

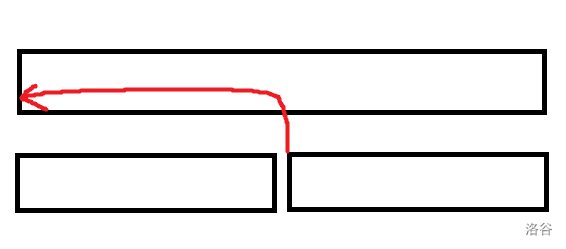
利用左侧查询的优势：可以发现询问的部分如果是某个线段树结点的后缀，则可以不用暴力，而是用持久化平衡树的一次查询代替。

总时间复杂度 $O(n\log v+m\log^2v)$，空间复杂度 $O(n\log^2 v)$。

这个算法没有利用取模的特性，所以不优，在其他没有好的性质的题中是已知的最优做法。

利用以上技巧极限卡常后，期望得分推测为 55~85 分。

算法 6

我们考虑使用 “全局平衡” 的思想，类似于树链剖分套线段树的那种问题，每次查询如果需要在 $O(\log n)$ 个子问题上花费 $O(\log n)$ 的代价二分，导致复杂度是 $O(\log n) \times O(\log n)=O(\log^2n)$，如果将两种二分的结构套起来，构造出一种常数层减半的结构，就可以做到 $O(\log n) + O(\log n)=O(\log n)$。

我们在这个问题上，尝试将一开始的持久化平衡树的做法进行拓展，使得其可以进行区间查询，并且将第二，四种暴力做法的思想结合进去，即利用每次只会发生 $O(\log v)$ 次取模的特性。

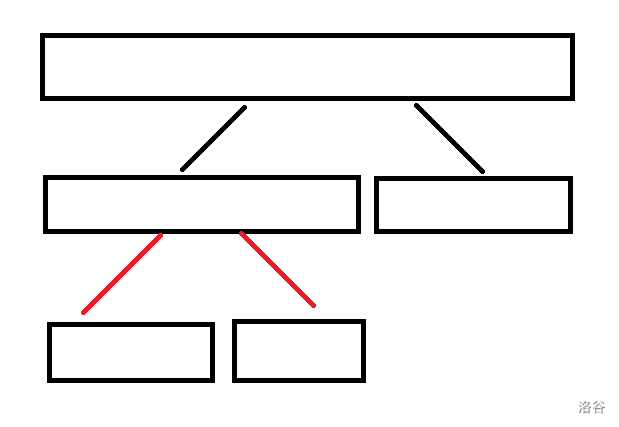
我们在持久化平衡树上维护每条边的边权，有两种颜色的边，分别是红色和黑色。红色的边的含义是下方结点是某次取模导致的区间复制复制产生的，黑色的边的含义是正常持久化平衡树的边。

每个叶子结点到根结点的路径上最多只有 $O(\log v)$ 条红色的边，因为每走一次红色的边相当于找到了一次发生取模的事件，取模的性质保证只能发生 $O(\log v)$ 次取模。同时由于持久化平衡树是平衡树，所以可以保证每个叶子结点到根结点的路径上最多有 $O(\log v)$ 条黑色的边。

具体实现的时候，我们需要对每条红色的边记录下这条边是序列上哪个位置产生的，持久化平衡树的重新平衡（如旋转）仅限于对黑色的边，对红色的边是不做重新平衡的。平衡操作可以看做是产生新的边，以及将原本两条新的边压缩为一条边。由于我们是通过红色的边来找到每次取模的位置的，所以重新平衡的时候对红色的边做平衡操作会使得找取模位置的时候少找了一些，只能对黑色的边做操作。

每次查询 $[l,r]$ 区间，输入 $v$ 时，先在 $l$ 位置的持久化平衡树根结点上开始查询 $v$，在查询的过程中每次走一条红色的边则意味着发生了一次取模，走黑色的边则是为了保证持久化平衡树的深度所必须走的。这样我们可以用 $O(\log v)+O(\log v)=O(\log v)$ 的时间复杂度找到 $[l,r]$ 区间查询时所发生的所有取模事件。在递归查询的过程中如果发现走到了一条时间 $>r$ 的红色的边，则不需要继续递归了。

其实可以进一步解释本题做法，我们需要维护一个 DAG 结构，使得从任何点出发，该 DAG 深度是 $O(\log v)$ 的。虽然暴力的计算图的 DAG 深度是 $O(n)$ 的，但是我们只关心取模的位置，所以对于不是取模的操作可以将其合并在一起来减少 DAG 的深度。利用持久化平衡树深度以及取模次数的性质，可以构造出一个满足我们要求的 DAG 结构，每次查询本质上是在预处理好的深度 $O(\log v)$ 的 DAG 结构上进行 DFS。

本做法对于其他持久化平衡树做法有显著优势，因为其他做法需要多次查询持久化平衡树，本做法只需要一次查询，虽然本做法的平衡树由于“重量平衡”的性质所以常数比正常平衡树大。

总时间复杂度 $O((n+m)\log v)$，空间复杂度 $O(n\log v)$。

期望得分 100 分。