自动搬运

查看原文

来自洛谷，原作者为

	顾z 得之我幸，失之我命

搬运于2025-08-24 21:22:01，当前版本为作者最后更新于2018-08-14 06:19:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

顾z

你没有发现两个字里的blog都不一样嘛 qwq

题目描述-->p1169 棋盘制作

题目大意

给定一个01棋盘,求其中01交错的最大正方形与矩形。

解题思路:

动态规划－－－悬线法

以下内容部分参考@Clove_unique

悬线法

用途:

解决给定矩阵中满足条件的最大子矩阵

做法:

用一条线(横竖貌似都行)左右移动直到不满足约束条件或者到达边界

定义几个东西:

$left[i][j]$:代表从$(i,j)$能到达的最左位置

$right[i][j]$:代表从$(i,j)$能到达的最右位置

$up[i][j]$:代表从$(i,j)$向上扩展最长长度.

递推公式：

$$left[i][j]=max(left[i][j],left[i-1][j]$$ $$right[i][j]=min(right[i][j],right[i-1][j]$$

至于为什么递推公式中考虑上一层的情况？

是因为up数组的定义,up数组代表向上扩展最长长度, 所以需要考虑上一层的情况.

解决

求解正方形&&长方形的情况即可。

题目要求01交错,所以"!="即可

-------------------代码-------------------

#include<bits/stdc++.h>
#define IL inline
#define RI register int
#define maxn 2001
using namespace std;
IL void read(int &x){
	int f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while(s<='9'&&s>='0'){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int res[maxn][maxn],left[maxn][maxn],right[maxn][maxn],up[maxn][maxn];
int n,m,ans1,ans2;
int main()
{
	read(n),read(m);
	for(RI i=1;i<=n;i++)
		for(RI j=1;j<=m;j++)
			{
				read(res[i][j]);
				left[i][j]=right[i][j]=j;
				up[i][j]=1;
			}
	for(RI i=1;i<=n;i++)
		for(RI j=2;j<=m;j++)
			if(res[i][j]!=res[i][j-1])
				left[i][j]=left[i][j-1];//预处理左边界
	for(RI i=1;i<=n;i++)
		for(RI j=m-1;j>0;j--)
			if(res[i][j]!=res[i][j+1])
				right[i][j]=right[i][j+1];//预处理右边界
	for(RI i=1;i<=n;i++)
		for(RI j=1;j<=m;j++)
			{
				if(i>1&&res[i][j]!=res[i-1][j])
				{
					left[i][j]=max(left[i][j],left[i-1][j]);
					right[i][j]=min(right[i][j],right[i-1][j]);
					up[i][j]=up[i-1][j]+1;
				}
				int a=right[i][j]-left[i][j]+1;	//横向长度
				int b=min(a,up[i][j]);//竖向长度
				//printf("a:%d b:%d\n",a,b);
				ans1=max(ans1,b*b);//正方形
				ans2=max(ans2,a*up[i][j]);//长方形
			}
	printf("%d\n%d",ans1,ans2);
}

悬线法题目:P1169 棋盘制作 p4147 玉蟾宫 p2701 巨大的牛棚 p1387 最大正方形

UPD

2018.09.26

Q ：如图这种情况下,我们根据状态转移方程求出的是黑色部分的面积.而实际上我们更大的面积为红色部分,这样的话,悬线法不就错了?

(如果你也有这方面的疑惑,请细读下面的话)

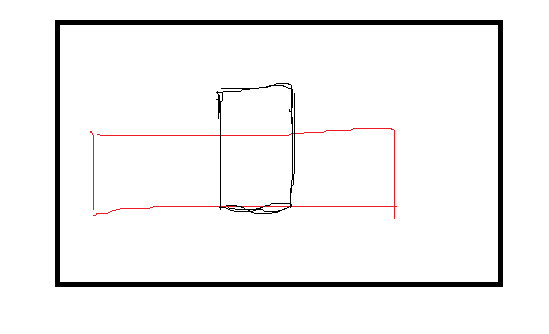
A：红色部分会被考虑到.

考虑我们代码中的这一部分

if(i>1&&res[i][j]!=res[i-1][j])
{
	left[i][j]=max(left[i][j],left[i-1][j]);
	right[i][j]=min(right[i][j],right[i-1][j]);
	up[i][j]=up[i-1][j]+1;
}

if语句执行的条件是$res[i][j]!=res[i-1][j]$,即只有满足条件的情况下我们才能更改当前位置$(i,j)$的$left$数组与$right$数组.

而不满足条件时,我们当前位置$(i,j)$的$left,right,up$数组并不会改变.

所以说当再次进行状态转移的时候,我们又能根据图中这些未被更新的点(即蓝色部分)的数组去求解出红色部分的面积.

还有一点需要注意的是,在某一行的一段的合法序列中,他们的$left$数组与$right$数组所指位置相同.(这个根据状态转移方程应该不难理解.

例如这样,这一段合法序列中位置的$left[i][j]$所指位置皆为红色部分,$right[i][j]$所指位置皆为蓝色部分.

如果不能理解的话可以私信问我的 qwq.

已经尽力写的很详细啦