自动搬运

查看原文

来自洛谷，原作者为

	immix *防衛本能だ。　*

搬运于2025-08-24 23:09:12，当前版本为作者最后更新于2025-02-04 18:44:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

更好的体验

类似题目：

• P10513 括号
• P8765 [蓝桥杯 2021 国 AB] 翻转括号序列

区间翻转，区间最长合法括号子串

P11657 「FAOI-R5」datealive

给定一个长度为 $n$ 的括号序列，支持 $m$ 次操作：

1. 翻转 $[l,r]$ 中的括号，即 ( 变 )，) 变 (。
2. 查询子串 $[l,r]$ 最长合法括号子串的长度。

$n\le 4\times 10^6,m\le 1\times 10^5$，保证操作类型随机。

对于翻转来说。我们只用额外维护一个节点保存取反之后的结果，然后翻转操作交换两个节点的内容，不是本题的难点，我们考虑如何求出一个区间的最长合法括号子串。

利用线段树的分治结构，我们能求出了只在左右区间内的结果，考虑如何处理横跨区间两边的子串。

我们知道：一个括号序列能匹配都匹配完之后剩下一定是一段前缀 ) 和后缀 (。（要不然就还有能匹配的部分）

比如序列 (())))()(() 最后留下的就是 ))(。

不失一般性，假设左区间在右边剩下的 ( 个数更多。

假设匹配了 $k$ 个，我们只需要找到左区间简化后的第 $k+1$ 个 (（从右边数）和右边的第一个 (（从左边数）。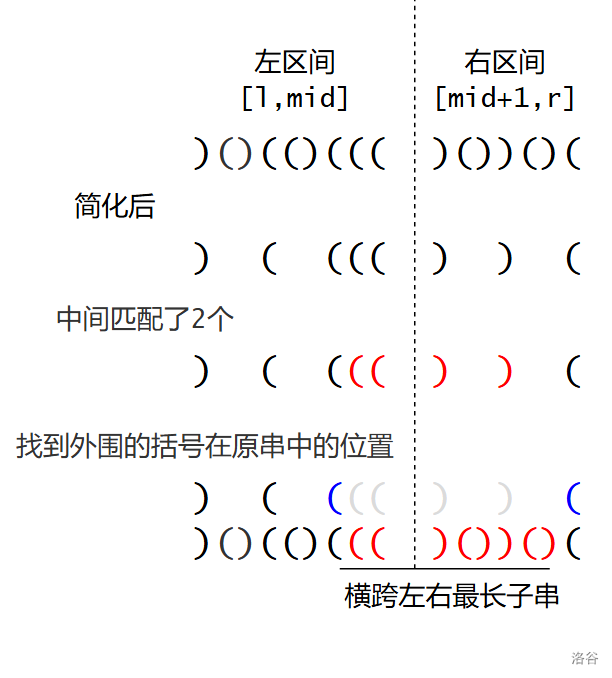

我们讨论实现找到这些括号位置的细节。

我们发现，对于一个固定起点来说，开头剩余的 ) 个数单调不下降。（因为再也没有字符能和它匹配了）

同样地，对于一个固定终点来说，结尾剩余的 ( 个数也单调不下降。

基于这个单调性，我们可以用线段树二分，花费 $O(\log n)$ 的代价找到这些括号的位置。

对于 ) 来说，因为是固定起点单调不降，所以只能左往右找到第 $k$ 个 )（如果反过来，) 就有可能被前面的 ( 闭合，难以找到实际的位置） ，而对于 ( 就只能从右往左找了。

直接线段树二分也是可行的，这里提供一种更简单的二分。

对于区间 $[l,r]$ 和一个完全包含它的节点 $o$：

先花 $O(\log n)$ 把 $[l,r]$ 拆分成 $O(\log n)$ 个区间。

struct Node{
    int o,l,r;  // 包含 [l,r] 的线段树节点编号和该节点维护区间
    int cntL,cntR,ans; // 左边剩下的)，右边剩下的(，答案
};
Node stk[10000];int tp;
void find_nodes(int o,int ql,int qr,int op){
    if(ql<=t[o][op].l&&t[o][op].r<=qr){stk[++tp]=t[o][op];return;}
    int lch=o<<1,rch=o<<1|1;
    int mid=(t[o][op].l+t[o][op].r)>>1;
    pushdown(o);
    if(ql<=mid)find_nodes(lch,ql,qr,op);
    if(qr> mid)find_nodes(rch,ql,qr,op);
}

然后以找到从左边数第 $k$ 个 ) 为例： 找到 $O(\log n)$ 段中第一个达到 $k$ 个 ) 的，然后在这一段里面进行二分找到真正的分界点，这样二分就保证了时刻处理的都一定是完整的节点，直接用一个 while 循环就足够解决问题。

复杂度仍然是 $O(\log n)$。

struct Node{
    int o,l,r;  // 包含 [l,r] 的线段树节点编号和该节点维护区间
    int cntL,cntR,ans; // 左边剩下的)，右边剩下的(，答案
};

// 找到 [ql,qr] 中第 k 个剩的右括号所在的位置（最靠左的那个）
int getkth_L(int o,int ql,int qr,int op,int k){
    tp=0; find_nodes(o,ql,qr,op);
    for(int i=1;i<=tp;i++){
        if(stk[i].cntL >= k){ // 在 i 处二分即可。
            int l = stk[i].l, r = stk[i].r;
            o = stk[i].o;
            while(l<r){
                pushdown(o); // 记得 pushdown
                int mid=(l+r)>>1;
                int lch=o<<1,rch=o<<1|1;
                if(t[lch][op].cntL >= k)r=mid,o=lch;
                else k=k-t[lch][op].cntL+t[lch][op].cntR,l=mid+1,o=rch;
            }
            return l;
        }
        k = k - stk[i].cntL + stk[i].cntR;
    }
    assert(0); // 我们保证一定存在这样的位置
    return -1;
}

有了这个，我们就可以开始写 merge 函数，用于合并两个节点了。

Node merge(const Node& p,const Node& q,int op){
    int elim = min(p.cntR, q.cntL);
    Node ret{min(p.o,q.o)>>1,p.l,q.r,p.cntL+q.cntL-elim,p.cntR+q.cntR-elim,max(p.ans,q.ans)};
    int newans;
    
    if(p.cntR == q.cntL){
        newans =    (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r) 
                  - (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
    }
    else if(p.cntR >= q.cntL){ 
        // q 的被消耗完了
        newans =    (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r) 
                  - (getkth_R(p.o,p.l,p.r,op,q.cntL+1)+1) + 1;
    }
    else{
        // p 的被消耗完了
        newans =    (getkth_L(q.o,q.l,q.r,op,p.cntR+1)-1) 
                  - (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
    }
    ret.ans = max(ret.ans, newans);
    return ret;
}

分类讨论哪边的括号被消耗完，找到对应的位置，算出横跨的长度更新答案就好了。

建树复杂度 $T(n)=2T(n/2)+O(\log n) = O(n)$，查询复杂度 $O(\log^2 n)$。 总复杂度 $O(n+q\log^2 n)$。

这道题空间卡的也比较紧（主要是 $n$ 太大了）。

完整代码：

#include<bits/stdc++.h>
using namespace std;

const int N = 4e6+6;
int a[N];
struct Node{
    int o,l,r;  // 包含 [l,r] 的线段树节点编号和该节点维护区间
    int cntL,cntR,ans; // 左边剩下的)，右边剩下的(，答案
};

Node t[N*4][2];bool tag[N*4];

void inv(int o){
    swap(t[o][0],t[o][1]);
    tag[o] = !tag[o];
}
void pushdown(int o){
    if(tag[o]){
        int lch=o<<1,rch=o<<1|1;
        inv(lch);inv(rch);
        tag[o]=0;
    }
}


Node stk[10000];int tp;
void find_nodes(int o,int ql,int qr,int op){
    if(ql<=t[o][op].l&&t[o][op].r<=qr){stk[++tp]=t[o][op];return;}
    int lch=o<<1,rch=o<<1|1;
    int mid=(t[o][op].l+t[o][op].r)>>1;
    pushdown(o);
    if(ql<=mid)find_nodes(lch,ql,qr,op);
    if(qr> mid)find_nodes(rch,ql,qr,op);
}

// 找到 [ql,qr] 中第 k 个剩的右括号所在的位置（最靠左的那个）
int getkth_L(int o,int ql,int qr,int op,int k){
    tp=0; find_nodes(o,ql,qr,op);
    for(int i=1;i<=tp;i++){
        if(stk[i].cntL >= k){ // 在 i 处二分即可。
            int l = stk[i].l, r = stk[i].r;
            o = stk[i].o;
            while(l<r){
                pushdown(o);
                int mid=(l+r)>>1;
                int lch=o<<1,rch=o<<1|1;
                if(t[lch][op].cntL >= k)r=mid,o=lch;
                else k=k-t[lch][op].cntL+t[lch][op].cntR,l=mid+1,o=rch;
            }
            return l;
        }
        k = k - stk[i].cntL + stk[i].cntR;
    }
    assert(0);
    return -1;
}

// 找到 [ql,qr] 中从右边看，第k个右边剩下的左括号所在的位置（最靠右的那个）
int getkth_R(int o,int ql,int qr,int op,int k){
    tp=0; find_nodes(o,ql,qr,op);
    for(int i=tp;i>=1;i--){
        if(stk[i].cntR >= k){ // 在 i 处二分即可。
            int l = stk[i].l, r = stk[i].r;
            o = stk[i].o;
            while(l<r){
                pushdown(o);
                int mid=(l+r)>>1;
                int lch=o<<1,rch=o<<1|1;
                if(t[rch][op].cntR >= k)l=mid+1,o=rch;
                else k=k-t[rch][op].cntR+t[rch][op].cntL,r=mid,o=lch;
            }
            return l;
        }
        k = k - stk[i].cntR + stk[i].cntL;
    }
    assert(0);
    return -1;
}


Node merge(const Node& p,const Node& q,int op){
    int elim = min(p.cntR, q.cntL);
    Node ret{min(p.o,q.o)>>1,p.l,q.r,p.cntL+q.cntL-elim,p.cntR+q.cntR-elim,max(p.ans,q.ans)};
    int newans;
    
    if(p.cntR == q.cntL){
        newans =    (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r) 
                  - (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
    }
    else if(p.cntR >= q.cntL){ 
        // q 的被消耗完了
        newans =    (q.cntR ? getkth_R(q.o,q.l,q.r,op,q.cntR)-1 : q.r) 
                  - (getkth_R(p.o,p.l,p.r,op,q.cntL+1)+1) + 1;
    }
    else{
        // p 的被消耗完了
        newans =    (getkth_L(q.o,q.l,q.r,op,p.cntR+1)-1) 
                  - (p.cntL ? getkth_L(p.o,p.l,p.r,op,p.cntL)+1 : p.l) + 1;
    }
    ret.ans = max(ret.ans, newans);
    return ret;
}

void build(int o,int l,int r){
    if(l==r){
        t[o][0] = {o,l,r, a[l]==1,a[l]==0,0};
        t[o][1] = {o,l,r, a[l]==0,a[l]==1,0};
        return;
    }
    int lch=o<<1,rch=o<<1|1;
    int mid=(l+r)>>1;
    build(lch,l,mid);build(rch,mid+1,r);
    t[o][0] = merge(t[lch][0],t[rch][0],0);
    t[o][1] = merge(t[lch][1],t[rch][1],1);
}
void modify(int o,int l,int r,int ql,int qr){
    if(ql <=l && r<=qr){
        inv(o);return;
    }
    pushdown(o);
    int lch=o<<1,rch=o<<1|1;
    int mid=(l+r)>>1;
    if(ql<=mid)modify(lch,l,mid,ql,qr);
    if(qr>mid) modify(rch,mid+1,r,ql,qr);
    t[o][0] = merge(t[lch][0],t[rch][0],0);
    t[o][1] = merge(t[lch][1],t[rch][1],1);
}

Node query(int o,int l,int r,int ql,int qr){
    if(ql<=l && r<=qr)return t[o][0];
    pushdown(o);
    int lch=o<<1,rch=o<<1|1;
    int mid=(l+r)>>1;
    if(qr<=mid)return query(lch,l,mid,ql,qr);
    if(ql>mid)return query(rch,mid+1,r,ql,qr);
    return merge(query(lch,l,mid,ql,qr),query(rch,mid+1,r,ql,qr),0);
}
    

int main(){
    ios::sync_with_stdio(0);cin.tie(0);
    int n,m;cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];

    build(1,1,n);
    int lastans = 0;
    while(m--){
        int op,l,r;cin>>op>>l>>r;
        l=(l+lastans)%n+1,r=(r+lastans)%n+1;
        if(l>r)swap(l,r);
        if(op==1){
            lastans = query(1,1,n,l,r).ans;
            cout << lastans << '\n';
        }
        else modify(1,1,n,l,r);
    }
    return 0;
}