自动搬运

查看原文

来自洛谷，原作者为

	yizcdl2357 OI(2018.12.30~2025.3.2)

搬运于2025-08-24 23:08:53，当前版本为作者最后更新于2025-01-25 18:33:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

不到 10min 胡出来了，感觉这题严格小于 T3 啊。

题意

一个长为 $n$ 的数轴，每次可以在两个点上分别插入左右括号，或者删除一对之前插入的括号。每次操作结束后你需要判断是否可以重排每格内的括号，使每格中的左括号排在右括号前，且同一次插入的左右括号互相匹配。

题解

记 $(i,j)$ 为左括号在 $i$、右括号在 $j$ 的一对括号。

注意到如果两对括号 $(i,j)(i,j')$ 左端点相同，那重排时应该使右括号靠右的那一对括号的左括号靠左（否则不优）。

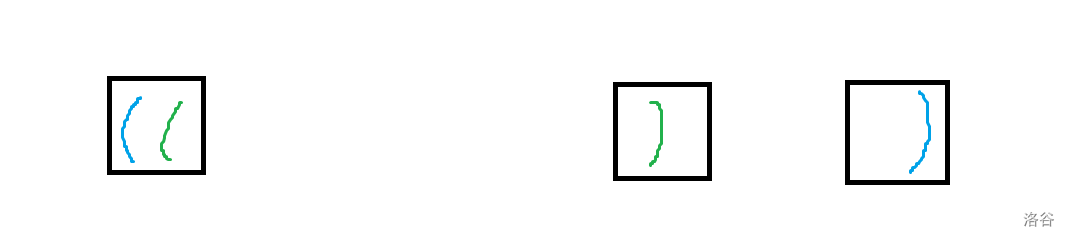
同理，如果两对括号 $(i,j)(i',j)$ 右端点相同，那重排时应该使左括号靠右的那一对括号的右括号靠左。

我们离线询问，把所有 $2\times(\text{操作 1 次数})$ 个括号按以下规则排序：

• 不同格内的括号，靠左的排前面；
• 同一格内的括号，左括号排在右括号前面；
• 同一格内的左括号，对应右括号位置越右的排在越前面；
• 同一格内的右括号，对应左括号位置越右的排在越前面。

这样，问题划归为括号两两不同格的情况。

如果没有删除操作，对一对在时刻 $id$ 输入的括号 $(i,j)$ 赋权值 $val=(j-i+1)\times 10^9+id$，则每两对括号权值不等，且若两对括号满足 $i<i',j'<j$ 则 $val_{i,j}>val_{i',j'}$。

用支持区间取 $\min$、单点查询的线段树维护长为 $n$ 的序列 $t$，每次插入一对括号 $(i,j)$ 时判断 $t_i$ 是否等于 $t_j$，若不等于则输出 No，若等于则输出 Yes 并将区间 $t_{i\sim j}$ 对 $val_{i,j}$ 取 $\min$ 即可。

有删除用线段树分治转化为只有加入，复杂度 $O(n\log^2 n)$。

代码

对括号排序后要 $n\leftarrow 2q$。

#include<bits/stdc++.h>
#define N 200000
#define int long long
#define ls id<<1,l,(l+r)>>1
#define rs id<<1|1,((l+r)>>1)+1,r
using namespace std;
struct xds{
	int a[8*N+5];
	int tp,stid[50000005],sta[50000005];
	inline void init(int id,int l,int r)
	{
		a[id]=1e18;
		if(r>l) init(ls),init(rs);
	}
	inline void add(int id,int x)
	{
		tp++;
		stid[tp]=id;
		sta[tp]=a[id];
		a[id]=x;
	}
	inline void ret()
	{
		a[stid[tp]]=sta[tp];
		tp--;
	}
	inline void upd(int id,int l,int r,int x,int y,int z)
	{
		if(r<x||l>y) return;
		if(x<=l&&r<=y){if(a[id]>z)add(id,z);return;}
		upd(ls,x,y,z),upd(rs,x,y,z);
	}
	inline int query(int id,int l,int r,int x)
	{
		if(r<x||l>x) return 2e18;
		if(l==r){return a[id];}
		return min(min(query(ls,x),query(rs,x)),a[id]);
	}
};
xds t;
int n,q,ans[4*N+5];
struct que{
	int tp,l,r,id,eid;
};
que a[N+5],lsh[2*N+5];
vector<que> ev[4*N+5];
inline bool cmp(que x,que y)
{
	if(x.l<y.l) return 1;
	if(x.l>y.l) return 0;
	if(x.r>y.r) return 1;
	if(x.r<y.r) return 0;
	if(x.r<0) return x.id<y.id;
	else return x.id>y.id;
}
inline void ins(int id,int l,int r,que x)
{
	if(r<x.id||l>x.eid) return;
	if(x.id<=l&&r<=x.eid){ev[id].push_back(x);return;}
	ins(ls,x),ins(rs,x);
}
inline void solve(int id,int l,int r)
{
	int _=t.tp;
	ans[id]=1;
	for(que i:ev[id])
	{
		if(t.query(1,1,2*q,i.l)!=t.query(1,1,2*q,i.r))
			{ans[id]=0;break;}
		t.upd(1,1,2*q,i.l,i.r,(i.r-i.l+1)*1e9+i.id);
	}
	if(r>l) solve(ls),solve(rs);
	while(t.tp>_) t.ret();
}
inline void getans(int id,int l,int r,int now)
{
	now&=ans[id];
	if(l==r){if(now==0)cout<<"No\n";else cout<<"Yes\n";return;}
	getans(ls,now),getans(rs,now);
}
signed main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n>>q;
	for(int i=1,x;i<=q;i++) 
	{
		cin>>a[i].tp;
		if(a[i].tp==1)
			cin>>a[i].l>>a[i].r,a[i].id=i;
		else cin>>x,a[x].eid=i;
	}
	for(int i=1;i<=q;i++)
	{
		lsh[i].tp=1;
		lsh[i].l=a[i].l,
		lsh[i].r=a[i].r,
		lsh[i].id=a[i].id,
		lsh[q+i].tp=1;
		lsh[q+i].l=a[i].r,
		lsh[q+i].r=-1e9+a[i].l,
		lsh[q+i].id=a[i].id;
	}
	sort(lsh+1,lsh+1+2*q,cmp);
	for(int i=1;i<=2*q;i++)
	{
		if(lsh[i].tp==0) continue;
		int now=lsh[i].id;
		if(lsh[i].r>=0) a[now].l=i;
		else a[now].r=i;
	}
//	for(int i=1;i<=q;i++) cout<<a[i].l<<' '<<a[i].r<<' '<<a[i].id<<' '<<a[i].eid<<'\n';
	for(int i=1;i<=q;i++)
	{
		if(a[i].tp==2) continue;
		if(a[i].eid==0) a[i].eid=q;
		else a[i].eid--;
		ins(1,1,q,a[i]);
	}
	t.init(1,1,2*q);
	solve(1,1,q);
	getans(1,1,q,1);
	return 0;
}/*8 2
1 1 4
1 4 4
*/

想借这篇题解总结一下备战省选的第一场比赛。

• 细节吃完了。A 一开始没看到 $m$ 的限制被控一小会；B 先想了一个假做法只有 60pts，不能处理重根；后来才想到生成函数。D 不知道如何处理多个括号在同一格的情况。
• • 以后思考一道题的同时想这个做法暂时不好处理的细节，敲代码前在草稿纸上把这些细节玩清楚、最好能把一组有一定强度的小样例玩清楚了再开写。
• 调试时间长于敲代码。调不出来的原因（如果不是细节的话）主要是想不到 hack 数据。
• • 在省选时这种情况多半可以通过大样例解决。
  • 我在这场比赛中的处理方法同样值得借鉴：把比较可能出错的部分替换成暴力，然后逐块换回原来的代码，这样可以精确定位到哪一个代码块有问题。

希望和我一样手跟不上脑子的 OIer 能有所收获，也祝各位省选 rp++。