自动搬运

查看原文

来自洛谷，原作者为

	cancan123456 怄火。挥手。转圈。街舞。跳跳。献吻。跳绳。激动。发抖。磕头。爱情。飞吻。左太极。右太极。回头。

搬运于2025-08-24 23:08:50，当前版本为作者最后更新于2025-02-10 16:32:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

感觉不难啊，为什么评黑呢？

首先我们手玩一下，可以感受到小球的运动大概这样：

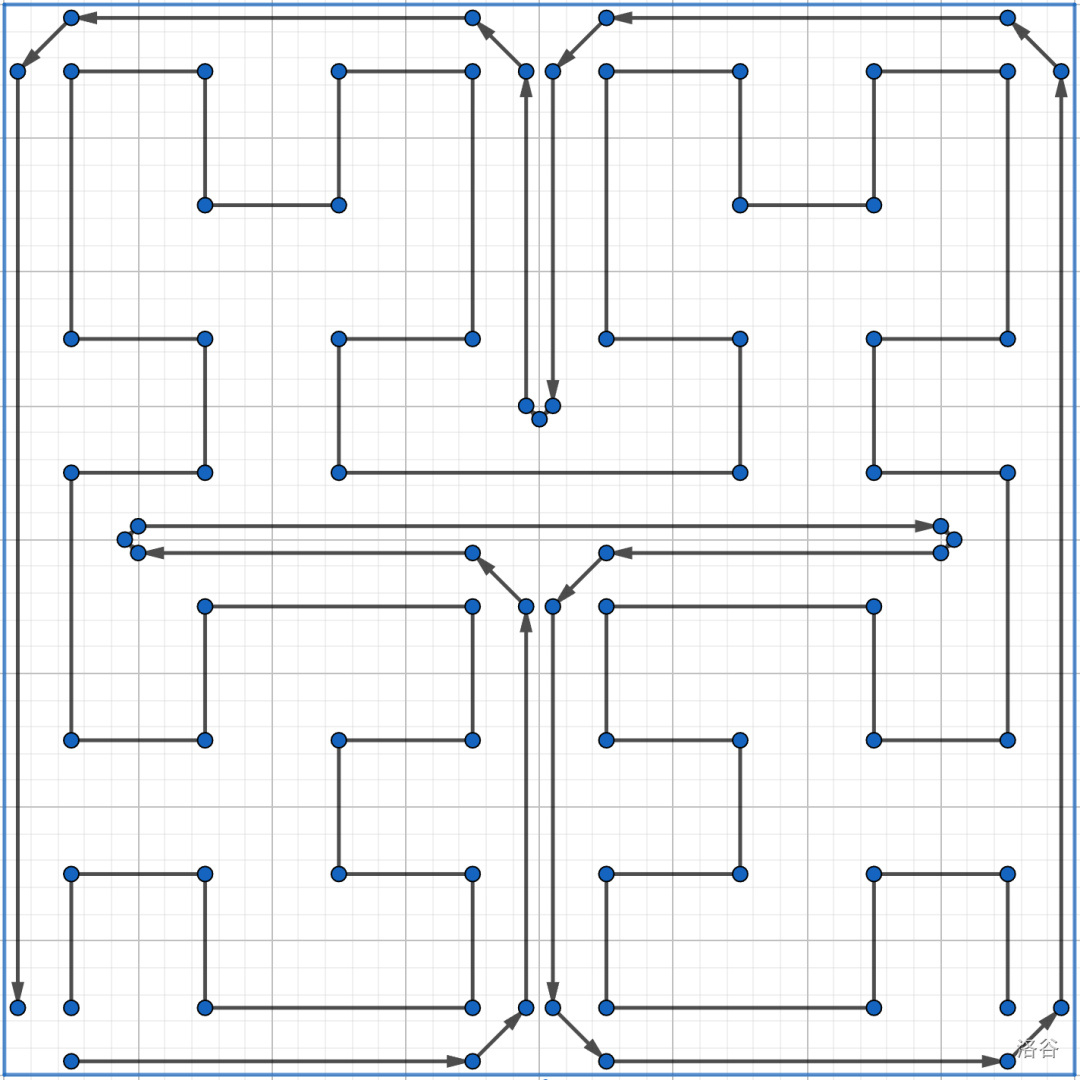
那么我们只需要算出这几段线的长度，就能递归下去求解子问题了，线段长度的计算可以 DP 做到 $O(n)$。

然后来考虑一下子问题的形式，有三类子问题。

1. $[0,2^{n+1}]\times[0,2^{n+1}]$ 是一个顺时针旋转 $90d_1^\circ$ 的 $n$ 阶 Hilbert 曲线，$[0,2^{n+1}]\times[-2^{n+1},0]$ 是一个顺时针旋转 $90d_2^\circ$ 的 $n$ 阶 Hilbert 曲线，小球从 $(1,0)$ 出发，初速度为 $(1,1)$，求运动 $t$ 秒后的位置，保证运动中 $x$ 坐标不超过 $2^{n+1}$。
2. $[0,2^{n+1}]\times[0,2^{n+1}]$ 是一个顺时针旋转 $90d^\circ$ 的 $n$ 阶 Hilbert 曲线，$y=0$ 是边界，小球从 $(1,0)$ 出发，初速度为 $(1,1)$，求运动 $t$ 秒后的位置，保证运动中 $x$ 坐标不超过 $2^{n+1}$。
3. $[0,2^{n+1}]\times[0,2^{n+1}]$ 是一个顺时针旋转 $90d^\circ$ 的 $n$ 阶 Hilbert 曲线，小球从 $(2^n,1)$ 出发，初速度为 $(1,1)$，求运动 $t$ 秒后的位置，保证运动中 $y$ 坐标不低于 $1$。

怎么求解这三类子问题呢，首先特判 $n=1$，打表或者直接模拟可以做到 $O(1)$。

还是考虑分治，对于一类子问题，考虑小球的轨迹（例如 $n=3,d_1=1,d_2=2$）：

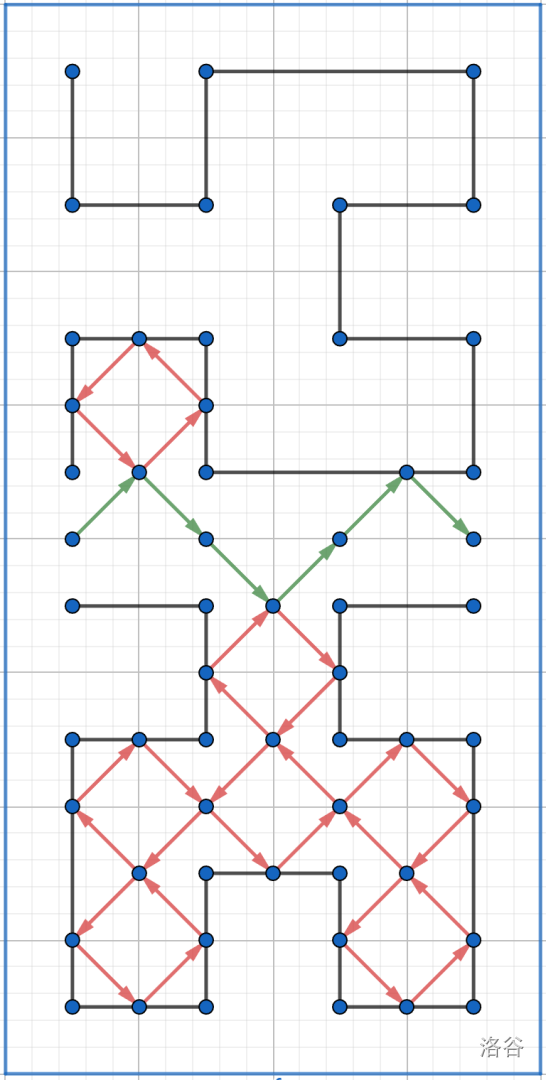
考虑怎么分解成 $n-1$ 的问题，从 $(2^n,-1)$ 这个点把路径分为前中后三个部分，前和后部分直接就是 $n-1$ 的一类子问题，中间部分是三类子问题。

对于二类子问题，仍然是同样的思路，把路径从 $(2^n,1)$ 拆分成三段，前后段是二类子问题，中间段是三类子问题。

对于三类子问题，需要对 $d$ 分讨。

1. $d=0$ 时，拆分成 $\begin{cases}(2^n,1)\to(2^n,2^n-1)\\(2^n-1,2^n)\to(1,2^n)\\(1,2^n)\to(2^n-1,2^n)\\(2^n,2^n+1)\\(2^n+1,2^n)\to(2^{n+1},2^n)\\(2^{n+1},2^n)\to(2^n+1,2^n)\\(2^n,2^n-1)\to(2^n,1)\end{cases}$ 七段，除了第四段每一段都是一类子问题。
2. $d=2$ 时，拆分成 $\begin{cases}(2^n,1)\to(2^n,2^n-1)\\(2^n,2^n-1)\to(2^n,1)\end{cases}$ 两段，每一段都是一类子问题。
3. $d=1$ 或 $3$ 时，此时 $t$ 一定为 $0$，直接返回 $(2^n+1,0)$ 即可。

对这些拆分合法性的证明繁而不难，只需要归纳即可，注意拆分在 $n=1$ 时会失效。

为了计算出 $t$ 秒后小球走到了哪一阶段，我们需要计算出这三类问题中 $t$ 的最大值，而这种问题可以通过 DP 解决，就是需要设一堆状态。

每次递归 $n$ 都减 $1$，所以时间复杂度为 $O(mn)$，可以通过此题。

#include <cstdio>
#include <utility>
using namespace std;
const int N = 35;
typedef long long ll;
ll f[N], g[N], h[N], sf[N], f0[N], f1[N], g0[N], g1[N], h0[N], h1[N], sh[N];
void pre() {
    f[1] = 6;
    sf[1] = 4;
    g[1] = 2;
    h[1] = 2;
    f0[1] = 6;
    f1[1] = 0;
    g0[1] = 2;
    g1[1] = 0;
    h0[1] = 2;
    h1[1] = 0;
    sh[1] = 4;
    for (int i = 2; i <= 30; i++) {
        f[i] = g[i - 1] + 1 + h[i - 1] + 1 + f[i - 1] + g[i - 1] + 2 + f[i - 1] + g[i - 1] + 1 + h[i - 1] + 1 + g[i - 1];
        sf[i] = h[i - 1] + 1 + f[i - 1] + g[i - 1] + 2 + f[i - 1] + g[i - 1] + 1 + h[i - 1];
        g[i] = f[i - 1] + 2 + g[i - 1];
        h[i] = h[i - 1] + 1 + g[i - 1] + g[i - 1] + 1 + h[i - 1];
        f0[i] = g0[i - 1] + g0[i - 1];
        f1[i] = g1[i - 1] + 1 + sf[i] + 1 + g1[i - 1];
        g0[i] = f0[i - 1] + g0[i - 1];
        g1[i] = f1[i - 1] + 2 + g1[i - 1];
        h0[i] = h0[i - 1] + h0[i - 1];
        h1[i] = h1[i - 1] + 1 + g[i - 1] + g[i - 1] + 1 + h1[i - 1];
        sh[i] = g[i - 1] + g[i - 1];
    }
}
pair < ll, ll > rotate(pair < ll, ll > point, pair < ll, ll > center, int dir) {
    dir = (dir % 4 + 4) % 4;
    if (dir == 0) {
        return point;
    }
    pair < ll, ll > delta = make_pair(point.first - center.first, point.second - center.second);
    if (dir == 1) {
        return make_pair(center.first + delta.second, center.second - delta.first);
    } else if (dir == 2) {
        return make_pair(center.first - delta.first, center.second - delta.second);
    } else {
        return make_pair(center.first - delta.second, center.second + delta.first);
    }
}
int get_UL(int dir) {
    static const int table[4] = {0, 2, 1, 3};
    return table[dir];
}
int get_UR(int dir) {
    static const int table[4] = {0, 1, 3, 2};
    return table[dir];
}
int get_DL(int dir) {
    static const int table[4] = {1, 0, 2, 3};
    return table[dir];
}
int get_DR(int dir) {
    static const int table[4] = {3, 1, 2, 0};
    return table[dir];
}
int upside_down(int dir) {
    if (dir % 2 == 0) {
        return dir ^ 2;
    } else {
        return dir;
    }
}
pair < ll, ll > solve1(ll, int, int, int);
ll get_time1(int, int, int);
pair < ll, ll > solve0(ll, int, int);
ll get_time0(int, int);
ll get_time00(int, int);
ll get_time01(int, int);
ll get_time_medium(int, int);
pair < ll, ll > solve2(ll, int, int);
pair < ll, ll > solve1(ll t, int n, int dir1, int dir2) {
    if (n == 1) {
        return solve0(t, n, dir1);
    }
    ll tt;
    tt = get_time1(n - 1, get_DL(dir1), get_UL(dir2));
    if (t <= tt) {
        return solve1(t, n - 1, get_DL(dir1), get_UL(dir2));
    }
    t -= tt + 1;
    tt = get_time_medium(n, upside_down(dir2));
    if (t <= tt) {
        pair < ll, ll > temp = solve2(t, n, upside_down(dir2));
        return make_pair(temp.first, -temp.second);
    }
    t -= tt + 1;
    pair < ll, ll > temp = solve1(t, n - 1, get_DR(dir1), get_UR(dir2));
    return make_pair((1 << n) + temp.first, temp.second);
}
ll get_time1(int n, int dir1, int dir2) {
    if (n == 1) {
        return get_time0(n, dir1);
    } else {
        return get_time00(n, dir1) + get_time01(n, upside_down(dir2));
    }
}
pair < ll, ll > solve0(ll t, int n, int dir) {
    if (n == 1) {
        if (dir == 0) {
            static const int table1[7] = {1, 2, 3, 2, 1, 2, 3};
            static const int table2[7] = {0, 1, 2, 3, 2, 1, 0};
            return make_pair(table1[t], table2[t]);
        } else {
            return make_pair(t + 1, t % 2);
        }
    }
    ll tt;
    tt = get_time0(n - 1, get_DL(dir));
    if (t <= tt) {
        return solve0(t, n - 1, get_DL(dir));
    }
    t -= tt + 1;
    tt = get_time_medium(n, dir);
    if (t <= tt) {
        return solve2(t, n, dir);
    }
    t -= tt + 1;
    pair < ll, ll > temp = solve0(t, n - 1, get_DR(dir));
    return make_pair((1 << n) + temp.first, temp.second);
}
ll get_time0(int n, int dir) {
    if (dir == 0) {
        return f[n];
    } else if (dir == 2) {
        return h[n];
    } else {
        return g[n];
    }
}
ll get_time00(int n, int dir) {
    if (dir == 0) {
        return f0[n];
    } else if (dir == 2) {
        return h0[n];
    } else {
        return g0[n];
    }
}
ll get_time01(int n, int dir) {
    if (dir == 0) {
        return f1[n];
    } else if (dir == 2) {
        return h1[n];
    } else {
        return g1[n];
    }
}
ll get_time_medium(int n, int dir) {
    if (dir == 0) {
        return sf[n];
    } else if (dir == 2) {
        return sh[n];
    } else {
        return 0;
    }
}
pair < ll, ll > solve2(ll t, int n, int dir) {
    if (n == 1) {
        if (dir == 0) {
            static const int tablex[5] = {2, 3, 2, 1, 2};
            static const int tabley[5] = {1, 2, 3, 2, 1};
            return make_pair(tablex[t], tabley[t]);
        } else {
            return make_pair(2, 1);
        }
    }
    ll tt;
    if (dir == 0) {
        tt = get_time1(n - 1, 2, 0);
        if (t <= tt) {
            pair < ll, ll > temp = solve1(t, n - 1, 2, 0);
            return make_pair((1 << n) + temp.second, temp.first);
        }
        t -= tt + 1;
        tt = get_time1(n - 1, 0, 3);
        if (t <= tt) {
            pair < ll, ll > temp = solve1(t, n - 1, 0, 3);
            return make_pair((1 << n) - temp.first, (1 << n) + temp.second);
        }
        t -= tt;
        tt = get_time1(n - 1, 1, 2);
        if (t <= tt) {
            pair < ll, ll > temp = solve1(t, n - 1, 1, 2);
            return make_pair(temp.first, (1 << n) - temp.second);
        }
        t -= tt + 1;
        if (t == 0) {
            return make_pair(1 << n, (1 << n) + 1);
        }
        t--;
        tt = get_time1(n - 1, 3, 2);
        if (t <= tt) {
            pair < ll, ll > temp = solve1(t, n - 1, 3, 2);
            return make_pair((1 << n) + temp.first, (1 << n) - temp.second);
        }
        t -= tt;
        tt = get_time1(n - 1, 0, 1);
        if (t <= tt) {
            pair < ll, ll > temp = solve1(t, n - 1, 0, 1);
            return make_pair((2ll << n) - temp.first, (1 << n) + temp.second);
        }
        t -= tt + 1;
        pair < ll, ll > temp = solve1(t, n - 1, 2, 0);
        return make_pair((1 << n) - temp.second, (1 << n) - temp.first);
    } else if (dir == 2) {
        tt = get_time1(n - 1, 3, 3);
        if (t <= tt) {
            pair < ll, ll > temp = solve1(t, n - 1, 3, 3);
            return make_pair((1 << n) + temp.second, temp.first);
        }
        t -= tt;
        pair < ll, ll > temp = solve1(t, n - 1, 1, 1);
        return make_pair((1 << n) - temp.second, (1 << n) - temp.first);
    } else {
        return make_pair(1 << n, 1);
    }
}
int main() {
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    pre();
    int n, m;
    scanf("%d %d", &n, &m);
    for (ll t; m != 0; m--) {
        scanf("%lld", &t);
        for (int i = 0; i < 4; i++) {
            ll tt = get_time0(n, i);
            if (t <= tt) {
                pair < ll, ll > ans = rotate(solve0(t, n, i), make_pair(1 << n, 1 << n), -i);
                printf("%lld %lld\n", ans.first, ans.second);
                break;
            } else {
                t -= tt + 1;
            }
        }
    }
    return 0;
}