自动搬运

查看原文

来自洛谷，原作者为

	canwen 你已经初三了初三了初三了 || 2025CSP RP++ || 争取今年不退役/ll

搬运于2025-08-24 23:08:29，当前版本为作者最后更新于2025-01-13 15:43:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

考察找规律。

写出打表程序，如下。

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e3 + 5;
int s[N];
bool pd(int a){
	int n = 0;
	while(a>0){
		s[++n] = a%10, a /= 10;
	}
	for(int i=1;i<=n/2;i++){
		if(s[i]!=s[n-i+1]) return 0;
	}
	return 1;
}
signed main(){
	int n, m;
	cin >> n >> m;
	for(int i=pow(10,n-1);i<=pow(10,n)-1;i++){
		for(int j=pow(10,m-1);j<=pow(10,m)-1;j++){
			if(pd(i*j)){
				cout << i << " " << j << endl;
				return 0;
			}
		} 
	}
	return 0;
}

不难发现两个答案可以形为首尾是 1，中间是 0，然后特判一点东西就能过。

代码如下：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e3 + 5;
int s[N];
bool pd(int a){
	int n = 0;
	while(a>0){
		s[++n] = a%10, a /= 10;
	}
	for(int i=1;i<=n/2;i++){
		if(s[i]!=s[n-i+1]) return 0;
	}
	return 1;
}
signed main(){
	int n, m;
	cin >> n >> m;
	if(n==1){
		cout << 1;
	}else if(n==2){
		cout << 11;
	}else{
		cout << 1;
		for(int i=1;i<=n-2;i++) cout << 0;
		cout << 1; 
	}
	cout << " ";
	if(m==1){
		cout << 1;
	}else if(m==2){
		cout << 11;
	}else{
		cout << 1;
		for(int i=1;i<=m-2;i++) cout << 0;
		cout << 1; 
	}
	
	return 0;
}

接下来是严谨的证明：

首先我们知道，$10^i$ 表示的数数位是 $i+1$。

那么有 $x\cdot y = (10^{n-1}+1) \cdot (10^{m-1}+1) = 10^{n+m-2}+10^{n-1}+10^{m-1}+1$。

这里我们假设 $n < m$，实际上 $n\ge m$ 交换一下 $m,n$ 的值同理可以证明。

那么上面的值可以画图表示成这样。

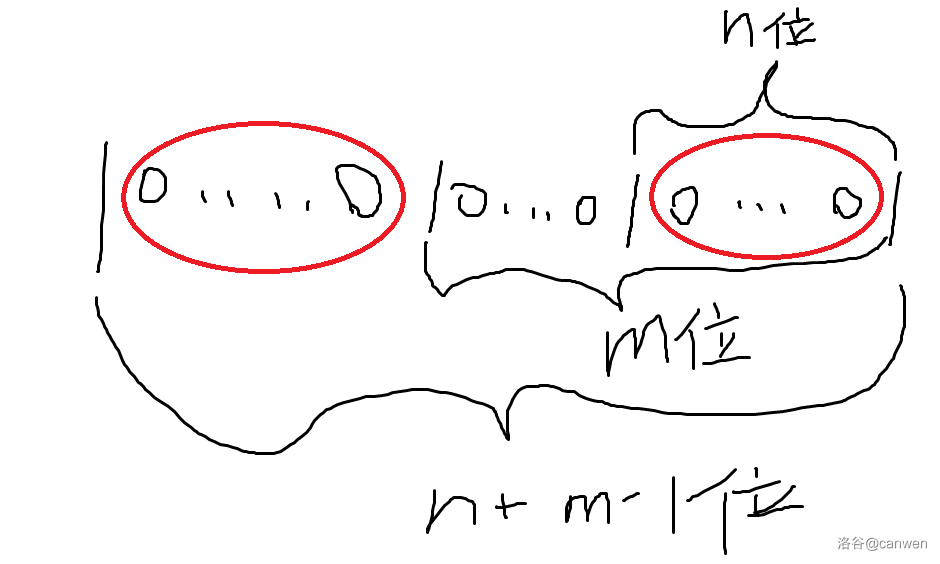
看起来很显然回文，小算一下。

显然形如 10...01 的是回文的。

左边红色圈里的 0 的数量可以表示为 $n+m-1-m-1=n-2$ 位。

右边红色圈里的 0 的数量也等于 $n-2$。

所以可以看出是回文的，所以如此构造可以使得 $x \cdot y$ 一定是回文数，得证。