自动搬运

查看原文

来自洛谷，原作者为

	DJN123 若是人生无悔，那该多无趣啊

搬运于2025-08-24 23:08:10，当前版本为作者最后更新于2025-04-13 17:02:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

看前面两篇题解有些地方没有说清楚，来发一篇解释一下这个思路的可行性。

题意

有一个 $n$ 个点，$m$ 条边的无向连通图，每个点有一定的高度要求，起点高度为零，每分钟可以经过一条边或原地不动，并同时使高度加一或减一或保持不变，并要求道达终点时高度为零。求：从 $1$ 到 $n$ 的最少耗时。

思路

观察题目，我们可以发现每一分钟可以改变 $1$ 的高度，也就是说，我们要到达 $a_i$ 的高度，所需时间最小为 $a_i$（就是一直上升的情况），也就是说，我们可以得到结论：在一直上升的情况下，高度就等于所花费时间。

但是，这个结论显然没有达到我们的要求。因为一条路径要求到终点时高度为零，因此我们不可能一直上升。但是也不难得出，在路径经过最高点后，我们就不再上升了。

举个栗子

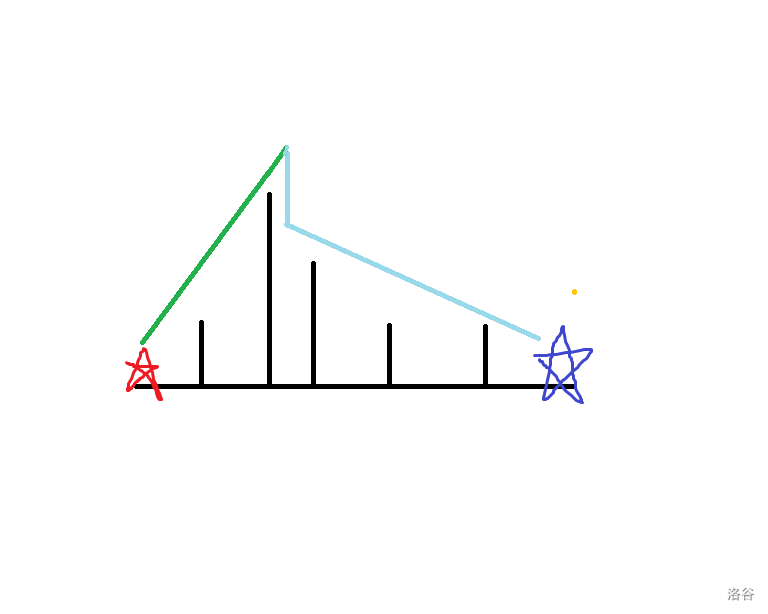
绿色这一段一直上升，而蓝色一段则需要一直下降，交汇的地方就是最高点，那么最高点高度 $h$ 就满足:总时间 $t_t = 2 \times h$。
怎么来的呢？绿色这一段的时间等于 $h$，这可以通过上述结论得来，而蓝色这一段，我们可以把它看成从终点上升到最高点，那么就符合条件限制了。

但我们肯定不可能去求一个路径的最高点，于是，我们发现，我们可以通过到达某个点的时间来设定这个路径的最高点，前面我们得到时间可以等于高度，那么我们对于任意一点 $i$，从起点一直上升到 $i$ 的时间为 $d1_i$，从终点一直上升到 $i$ 的时间为 $d2_i$ 于是我们可以得到路径的最高点为 $\max(d1_i , d2_i)$ 所以总耗时应该为 $\max(d1_i, d2_i) \times 2$。

解释一下

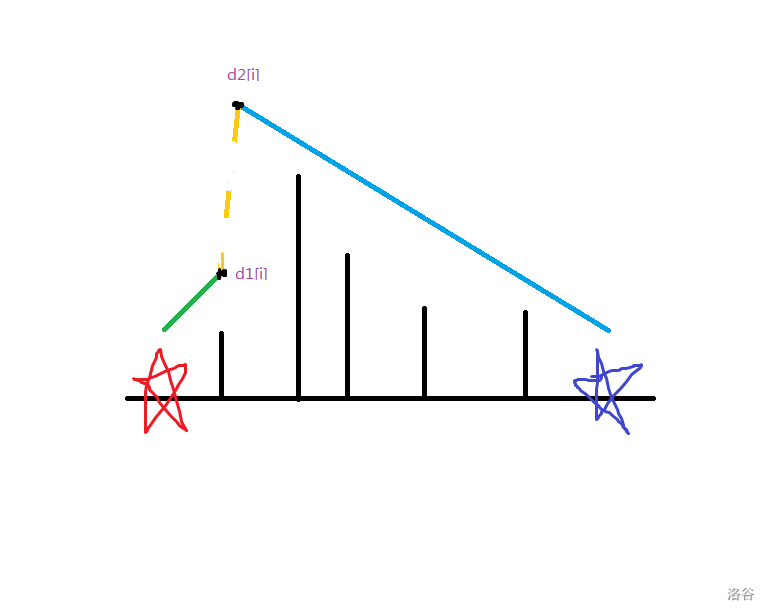
不难看出，由于两条路径的时间差，我们到达 $i$ 的高度就有差异（图中金色虚线），所以我们用 $\left | d1_i - d2_i \right |$ 来表示高度差，于是我们可以通过第 $i$ 个点求出路径时间为 $d1_i + d2_i + \left | d1_i - d2_i \right |$ 即 $\max(d1_i , d2_i) \times 2$。
这个思路还有没有缺陷呢？当然有了。

比如这个

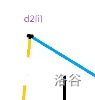
诶我们发现你头顶怎么尖尖的，当这条路径的长度（不是耗时），为奇数时，会出现这么个“尖顶”——（就是一段上升和一段竖直下降），这玩意的耗时为 $2$ 但如果我们用一段平飞来代替就可以使总耗时减一。怎么解决呢？我们可以“手动”加边，就是分别让 $i$ 与 $i - 1$“分担”一半，然后总耗时加上我们平飞的边，具体实现就是在取完 $\max(d1_i , d2_i) \times 2$ 后，再找 $i$ 的连点 $r$，取 $\max(d1_i , d2_r) \times 2 + 1$ 就解决了。
完结散花。

Code：

#include<bits/stdc++.h>
const int N = 200005, M = 400005 * 2;
using namespace std;
int in(){
	int ans = 0, f = 1;
	char c = getchar();
	while(c < '0' || '9' < c){
		if(c == '-')f = -1;
		c = getchar();
	}
	do{
		ans = (ans << 3) + (ans << 1) + c - '0';
		c = getchar();
	}while('0' <= c && c <= '9');
	return ans * f; 
}
struct node{
	int next, to;
}road[M];
int head[N], cnt;
void add(int x, int y){
	road[++cnt].next = head[x];
	road[cnt].to = y;
	head[x] = cnt;
}
int d1[N], d2[N], a[N];
bool vis[N];
int n, m, u, v;
void spfa(int u, int f[]){ 
	memset(vis, 0, sizeof(vis));
	f[u] = 0;
	queue<int>q;
	q.push(u);
	while(!q.empty()){
		int h = q.front();
		q.pop();
		for(int i = head[h];i;i = road[i].next){
			int r = road[i].to, ext = max(a[r] - f[h] - 1, 0);
			if(f[r] > f[h] + ext + 1){
				f[r] = f[h] + ext + 1;
				if(!vis[r]){
					q.push(r);
					vis[r] = 1;
				}
			}
		}
		vis[h] = 0;
	}
}
signed main(){
	n = in(), m = in();
	for(int i = 1;i <= n;i++)a[i] = in();
	for(int i = 1;i <= m;i++){
		u = in(), v = in();
		add(u, v), add(v, u);
	}
	memset(d2, 63, sizeof(d2));
	memset(d1, 63, sizeof(d1));
	spfa(1, d1);
	spfa(n, d2);
	int ans = INT_MAX;
	for(int i = 1;i <= n;i++){
		ans = min(max(d1[i] , d2[i]) * 2, ans);
		for(int j = head[i];j;j = road[j].next){
			int r = road[j].to;
			ans = min(max(d1[i], d2[r]) * 2 + 1, ans);
		}
	}
	cout<<ans;
}