自动搬运

查看原文

来自洛谷，原作者为

	floris 浸入我们残缺的时光

搬运于2025-08-24 23:07:46，当前版本为作者最后更新于2024-12-29 19:05:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

思路：

首先要判断是否可以建符合题目要求的树，显然，当图中存在环时，不能成为树，因此我们想到使用并查集维护，当输入的两个点的祖先相同时，因为这两个点还会连接，所以一定会成环，此时就结束掉程序；否则就可以建树。

因为这个题目中每条边都只被给出点的最短路径经过了一遍，因此，我们先将输入的点对直接建边（如下图蓝点），然后把剩下的点（下图红点）放在一边，再取出一对输入的点对（绿色点）：

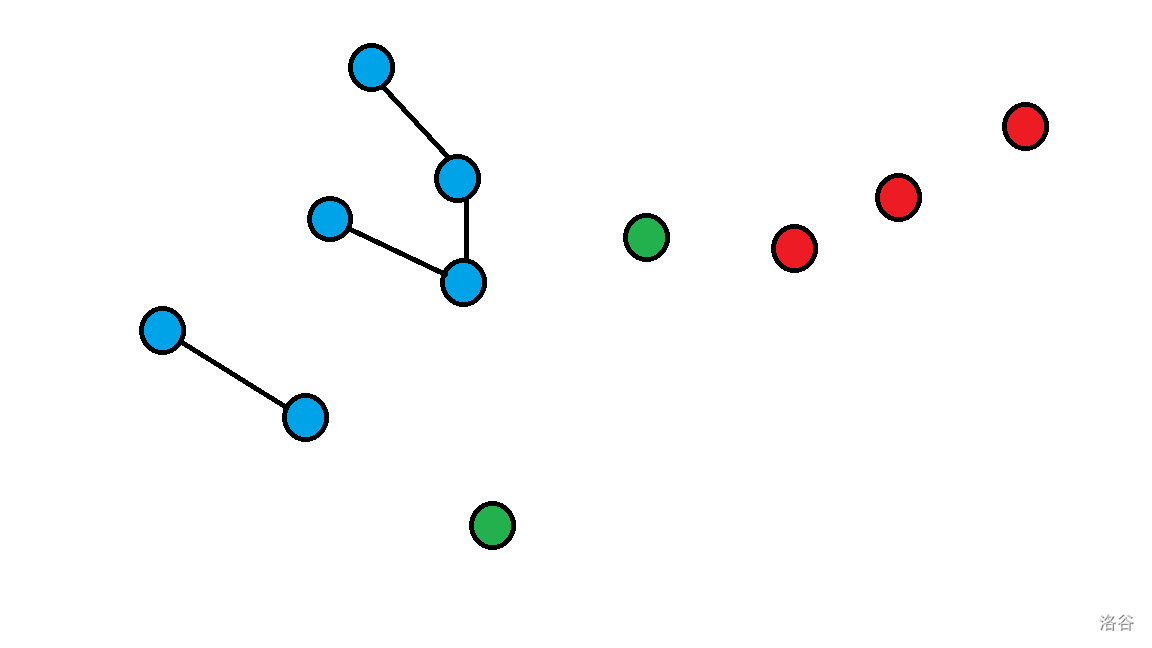
然后将绿色点作为头和尾将剩余点或树根串联起来，如图：

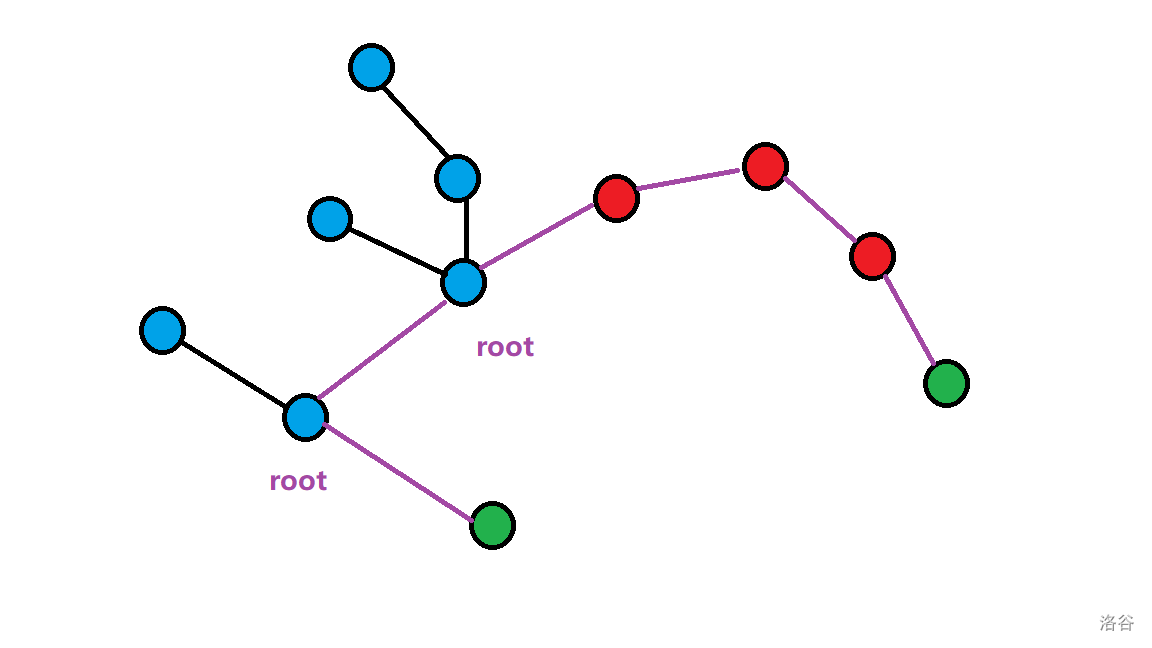
这样保证了每条边都可以走到，更重要的是，它代码好写。

写代码时要注意的是：每次连边后都要记录上一次连边的点，下一次要用。

code

#include<bits/stdc++.h>
using namespace std;
#define N 300005
int n,m,f[N];
int find(int x){
	if(f[x]==x) return x;
	return f[x]=find(f[x]);
}
int last,cnt=0;
struct node{
	int x,y;
}e[N];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) f[i]=i;
	for(int i=1;i<=m;i++){
		cin>>e[i].x>>e[i].y;
		if(find(e[i].x)!=find(e[i].y))f[find(e[i].y)]=find(e[i].x);
		else{
			cout<<"No"<<'\n';
			return 0;
		}
	}
	cout<<"Yes"<<'\n';
	for(int i=1;i<m;i++)cout<<e[i].x<<" "<<e[i].y<<'\n';
	last=e[m].x;
	for(int i=1;i<=n;i++){
		if(find(i)==i&&find(i)!=find(e[m].x)){
			cout<<last<<" "<<i<<'\n';
			last=i;
		}
	}
	cout<<e[m].y<<" "<<last<<'\n';
	return 0;
}