自动搬运

查看原文

来自洛谷，原作者为

	CraaazyShep セカイ的気候変動

搬运于2025-08-24 23:07:36，当前版本为作者最后更新于2024-12-23 23:24:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P11465 水上舞者索尼娅

提供一个考场上想出的，不使用快速幂和乘法逆元的倍增做法。

推导

方便起见我们称【一串香蕉（还剩 $x$ 根）】为 $x$ 级牌。

首先观察一下每张 $x$ 级牌使用后会发生什么：

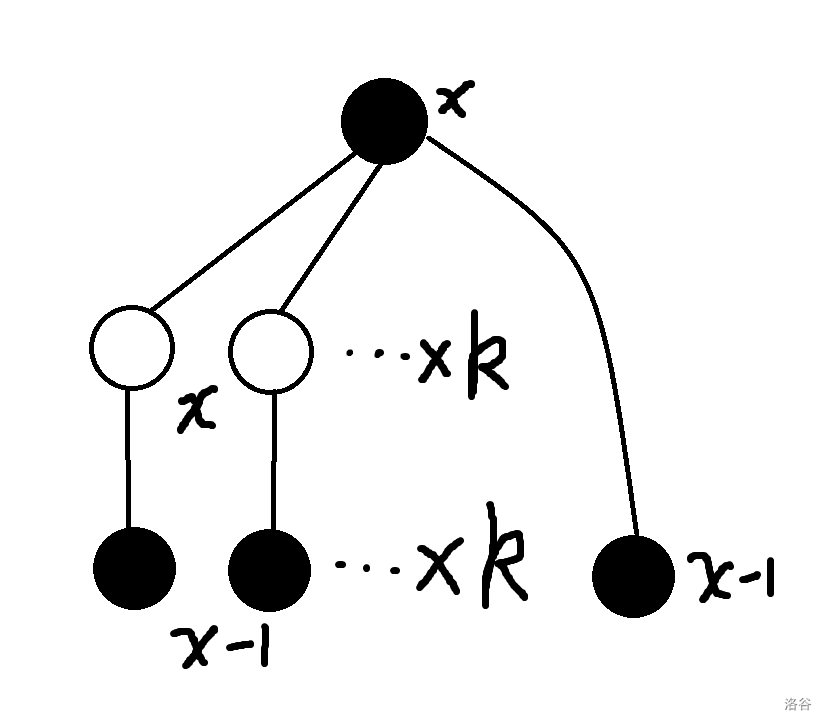
上图中黑色圆圈代表消耗为 $1$，白色圆圈代表消耗为 $0$。

观察到我们如果打出一张消耗为 $1$ 的 $x$ 级牌后，继续再把产生的消耗为 $0$ 的牌打光，过程中总计：

• 打出了 $k+1$ 次牌。
• （$x>1$ 时）最终产生 $k+1$ 张 $x-1$ 级牌。

我们把“将所有的消耗为 $1$ 的 $x$ 级牌转化为消耗为 $1$ 的 $x-1$ 级牌”称作一轮操作。

如果想要打光手中所有的牌，需要进行 $n$ 轮这样的操作。第 $i$ 轮操作中，初始手中会有 $(k+1)^{i-1}$ 张牌，每张牌都会产生 $k+1$ 次出牌，也就是说第 $i$ 轮操作最终产生总计 $(k+1)^i$ 次出牌。

那么显然的，答案就是：$\sum \limits_{i=1}^{n} (k+1)^i$。

实现

方便起见我们令 $m=k+1$，我们可以把求和的每一项都写成 $m$ 的 $2$ 的幂数次幂相乘的形式，我们以前 $8$ 项为例：

• $m^1,m^2,m^1m^2,m^4,m^1m^4,m^2m^4,m^1m^2m^4,m^8\dots$

将每项像这样分解开之后，我们可以发现第 $5$ 到 $8$ 项可以再作整理：

$\begin{aligned} m^1m^4+m^2m^4+m^1m^2m^4+m^8 &= (m^1+m^2+m^1m^2+m^4)m^4\\ &= m^4\cdot\sum \limits_{i=1}^{4} m^i \end{aligned}$

这启发了我们，当 $n=2^p$ 时有：

$\begin{aligned} \sum \limits_{i=1}^{2^p} m^i &= \sum \limits_{i=1}^{2^{p-1}} m^i + m^{2^{p-1}+1} + m^{2^{p-1}+2} + \cdots + m^{2^p}\\ &= \sum \limits_{i=1}^{2^{p-1}} m^i + m^{2^{p-1}}(m^1 + m^2 + \cdots + m^{2^{p-1}})\\ &= \sum \limits_{i=1}^{2^{p-1}} m^i + m^{2^{p-1}} \cdot \sum \limits_{i=1}^{2^{p-1}} m^i\end{aligned}$

于是我们可以使用倍增的思路来求出所有 $n$ 可以表示为 $2^p$ 时的结果。

当 $n=2^p$ 时，我们可以通过 $\sum \limits_{i=1}^{2^{p+1}} m^i = \sum \limits_{i=1}^{2^p} m^i + m^{2^p} \cdot \sum \limits_{i=1}^{2^p} m^i$ 来将 $n$ 倍增至 $2^{p+1}$。

如果 $n$ 不能表示为上述形式，则需要继续递归求解。

我们假设遇到了 $2^p < n < 2^{p+1}$ 的情况，可以列出式子：

$\begin{aligned} \sum \limits_{i=1}^{n} m^i &= \sum \limits_{i=1}^{2^p} m^i + m^{2^p+1} + m^{2^p+2} + \cdots + m^n\\ &= \sum \limits_{i=1}^{2^p} m^i + m^{2^p}(m^1 + m^2 + \cdots + m^{n-2^p})\\ &= \sum \limits_{i=1}^{2^p} m^i + m^{2^p} \cdot \sum \limits_{i=1}^{n-2^p} m^i \end{aligned}$

所以我们可以继续递归求出 $\sum \limits_{i=1}^{n-2^p} m^i$，再将其乘上 $m^{2^p}$ 加入答案即可。

像这样每次递归消掉一个最大的 $2^p$，最终即可得到答案。

时间复杂度为 $\mathcal{O}(T (\log n)^2)$。

代码

#include<bits/stdc++.h> 
using namespace std;
#define ll long long
const int mo=1e9+7;
ll t,n,k;
int calc(ll m,ll n){
    ll re=m,tot=1;   // re 为返回值，tot 标记求和到第几项。 
    ll mt=m;         // mt 为目前为止最大的 m 的 2 的幂数次幂。 
    while(tot*2<=n){
        re=(re+re*mt)%mo;
        tot*=2;
        mt=(mt*mt)%mo;
    }
    if(tot==n)return re;
    int rre=calc(m,n-tot);
    return (re+rre*mt)%mo;
}
void solve(){
    cin>>n>>k;
    ll m=k+1;
    ll ans=calc(m,n);
    cout<<ans<<endl;
    return;
}
int main(){
    cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

后日谈

这个做法在比赛当晚的讲评环节收获了出题人的不点名表扬，感到非常荣幸。实际上真的是因为我忘打印快速幂板子还不会乘法逆元才憋出来的。