自动搬运

查看原文

来自洛谷，原作者为

	zjy2008 else if

搬运于2025-08-24 23:07:11，当前版本为作者最后更新于2024-12-23 10:52:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

发现没有 sol，所以来复读一下官方题解。

考虑直线上方和下方点集构成的凸包，我们声称：

定理 1：令 $\epsilon \approx \dfrac{1}{2V}$，那么答案一定可以被表示成直线上方凸包的一条边向下平移 $\epsilon$ 或直线下方凸包的一条边向上平移 $\epsilon$。

证明是初中几何，这里就不再重复了。

接下来考虑两侧凸包的性质，只讨论下方的凸包，因为上方的凸包是同理的。

定理 2：凸包的点数不超过 $2\log_2 V$。

我们分 $2$ 步证明。在特殊性质 A 中，如果凸包包含 $(x,y)$，那么它一定包含 $(2x,2y)$，故除 $(0,0)$ 外左侧第一个点的横坐标一定大于 $\dfrac{V}{2}$，把 $(x_1,y_1)$ 平移到 $(0,0)$ 删去，凸包仍要满足上述性质，凸包点数为 $\log_2 V$。接下来，直接取平面中最接近直线的整点为原点，就可以得到 $2$ 个具有特殊性质 A 的平面，故凸包总点数不超过 $2\log_2 V$。

根据以上定理，我们只需要求出一些点使得它们能还原出原凸包即可求解。

首先，我们用 $2\log_2 V$ 次询问得到 $L(0)$ 和 $L(V)$。于是，问题变成了给你一个 $n\times (m+1)$ 大小的二维平面，保证直线和 $(0,0),(0,1)$ 这条线段有交，和 $(n,m),(n,m+1)$ 这条线段有交。

显然，如果有 $m\ge n$，有简单坐标变换：$(x,y)\to (x,y-\lfloor\dfrac{n}{m}\rfloor x)$，容易证明得到的结果是不变的（相当于凸包加直线）。

否则，可以通过 $2\log_2 \dfrac{n}{m}$ 次询问得到第一个 $L(x)\ge 1$ 和第一个 $L(x)\ge m$，然后交换坐标轴做子问题。大概形如下图：

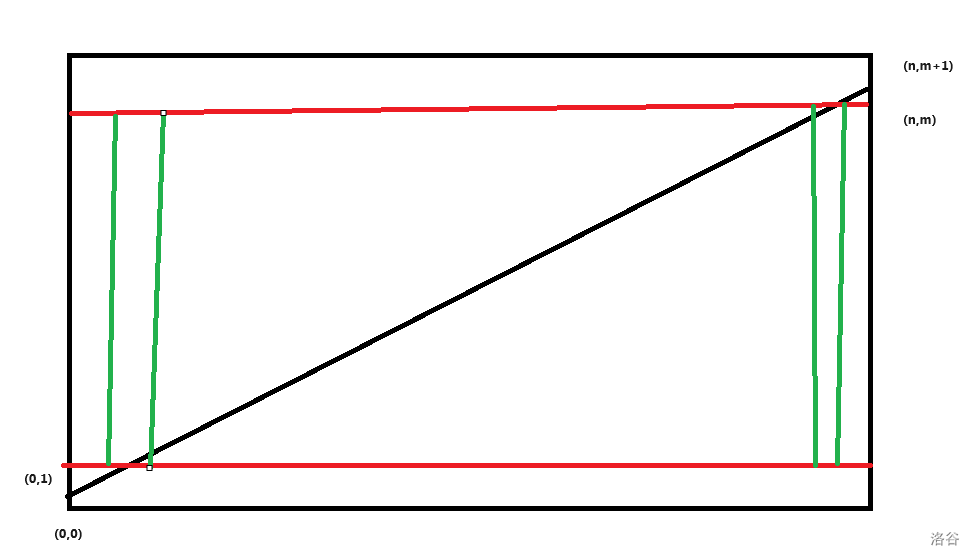
证明一下询问次数：$T(n,m)=T(m-1,(n-k)\bmod ({m-1}))+2\log_2\dfrac{n}{m}$，其中 $k\le 2\dfrac{n}{m}$, 显然是 $O(\log V)$ 的，因为 $n>m>0$，所以一定有 $n-k\ge m-1$，故每次 $n$ 至少减半。可以分析出查询次数 $\le 4\log V$。

关于时间复杂度：如果你用几个变量维护坐标变换，再 $O(\log)$ 凸包上查询是否存在点在直线下的话，可以做到 $O(\log V\log\log V)$，当然，$O(\log^2 V)$ 也是可以过的。

贴一个代码。