自动搬运

查看原文

来自洛谷，原作者为

	Milmon HN 高一最菜 OIer | 史上最菜的菜鸡 qaq | 快乐学习，认真刷题，努力进步！

搬运于2025-08-24 23:06:46，当前版本为作者最后更新于2025-01-07 14:28:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

Statement

给定一个包含 $n$ 个点的简单多边形和 $q$ 次询问，每次询问给定一条线段，判断该线段是否与多边形相交。

数据范围：$3 \leq n \leq 2 \times 10^5$，$1 \leq q \leq 2 \times 10^5$，所有坐标均为 $[0, 3 \times 10^4]$ 范围内的整数。

Solution

题目相当于给定 $n$ 条属于多边形的线段和 $q$ 条询问线段，需要对 $q$ 条询问线段分别判断是否存在多边形线段与其相交。

线段的相交问题不容易处理，考虑将线段变为直线。如果对横坐标分治，那么一条包含整个分治区间的线段就可以视作直线。这样每条线段就可以被放进 $O(\log V)$ 个分治区间中作为直线处理。只需要考虑两种情况：多边形的边被视作直线；询问的线段被视作直线。

先考虑多边形的边被视作直线的情况。由于是简单多边形，所以所有多边形的边必然不相交于非端点的位置，即分治区间内不存在交点。那么可以对多边形的边排序，对于每条询问的线段，一边二分一边判定是否于多边形的边相交即可。

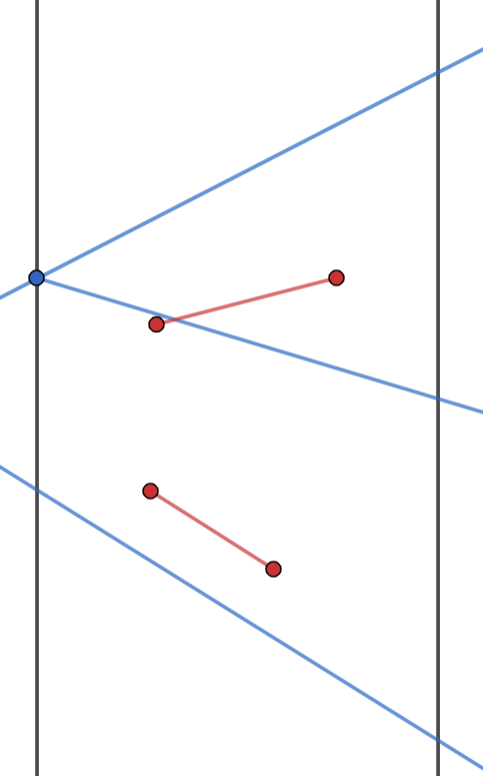
接下来只需要考虑询问的线段被视作直线的情况。此时多边形的边可以分为若干组，每组内部的线段首尾相连形成一条折线，组之间的线段不相交。

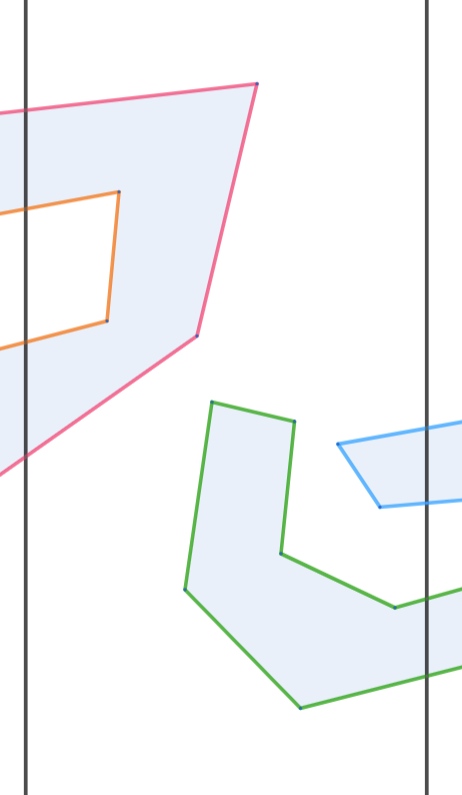
设分治区间的两条竖直的直线为 $L, R$。一种较为简单的情况是，询问的直线与某一侧的分治区间的直线（不妨设是 $L$）的交点位于某一条折线与 $L$ 相交的区间中，那么询问的直线就一定与这条折线相交。

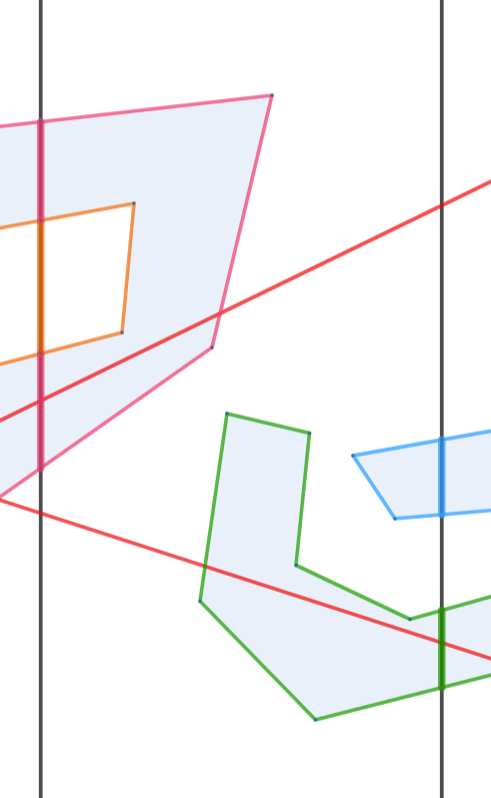
但是只考虑这种情况是不够的，因为可能存在这样的直线：

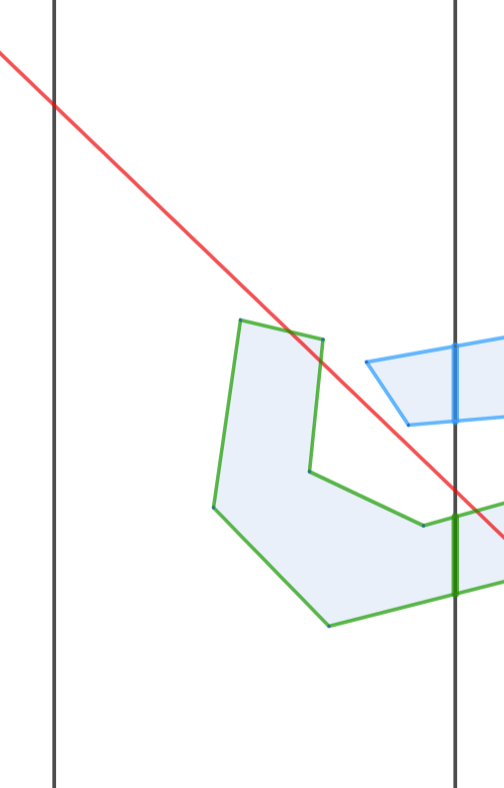
此时直线与绿色多边形相交，但不与绿色多边形与直线 $R$ 相交的区间相交。这种情况下，只要可以处理出询问的直线的右下方的所有折线中包含的点的凸包，再判断询问的直线是否与凸包相交即可。

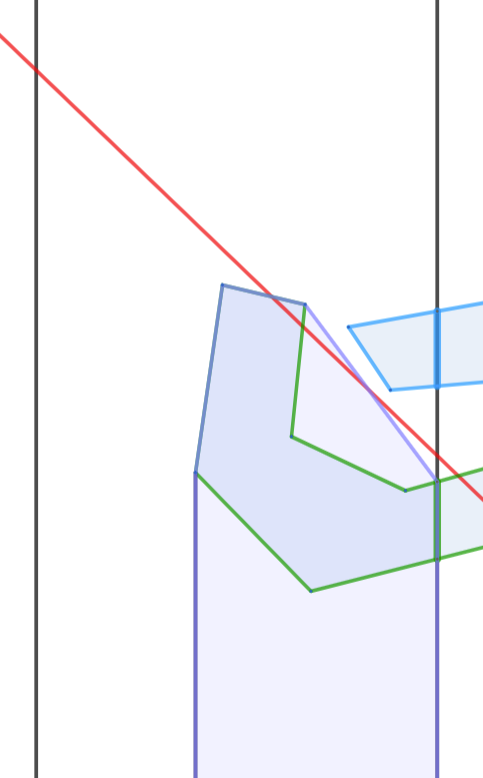
如何求出凸包？考虑按照每个折线与 $R$ 相交的区间排序，依次加入这些折线。加入一条折线时，找出折线中最靠左的不在凸包中的点 $X$，将原凸包中在 $X$ 的点的右侧的所有点删除，即可将折线的所有点依次插入凸包。

如何判断直线是否与凸包相交？二分找到与直线斜率最接近的一个点，并判断点和询问的直线的方向即可。

于是我们对左上、右上、左下、右下分别做一遍维护凸包的过程即可完成判断。

还需要注意的一点是，当询问的线段和多边形的边均垂直于横坐标轴时，两条线段均无法被分治处理，所以还需要额外对这些线段做一次排序、扫描线处理。

由于每条线段被分治到 $O(\log V)$ 个区间中，每个分治区间中的复杂度瓶颈在于排序，所以总时间复杂度为 $O((n + q) \log (n + q) \log V)$。

Note

代码太史山了就不放了，这里是一些做这道题的经历。我的代码总长 17.46 KiB，用时约十个小时，祝大家好运。

Solution (English)

The problem is equivalent to given $n$ line segments that belong to a polygon and $q$ query line segments. For each of the $q$ query line segments, we need to determine if any polygon edge intersects with it.

The problem of line segment intersection is not easy to handle, so let's consider transforming the line segments into straight lines. If we perform a divide-and-conquer based on the x-coordinates, a line segment that covers the entire divide-and-conquer interval can be treated as a straight line. This way, each line segment can be placed into $O(\log V)$ divide-and-conquer intervals and treated as a straight line. We only need to consider two situations: the polygon edges are treated as straight lines, and the query line segments are treated as straight lines.

First, let's consider the case where the polygon edges are treated as straight lines. Since it's a simple polygon, all the edges must not intersect at any point other than at their endpoints, meaning that no intersections exist within the divide-and-conquer intervals. We can then sort the polygon edges, and for each query line segment, we can perform binary search while simultaneously checking if it intersects with the polygon edges.

Next, we need to consider the case where the query line segments are treated as straight lines. In this case, the polygon edges can be divided into several groups, with the line segments within each group being connected end-to-end to form a polyline. The line segments between groups do not intersect.

Let the two vertical lines of the divide-and-conquer interval be $L$ and $R$. A relatively simple situation is when the intersection of the query line and one side of the divide-and-conquer interval's line (let's assume it is $L$) lies within the interval where a polyline intersects $L$. In this case, the query line will definitely intersect with this polyline.

However, considering only this case is not enough, because there may exist such lines:

In this case, the line intersects the green polygon but does not intersect the interval where the green polygon intersects the line $R$. In such cases, as long as we can process the convex hull of all the points contained within the polyline in the lower-right corner of the query line, we can then check if the query line intersects the convex hull.

To find the convex hull, consider sorting the polylines based on the intervals where they intersect with $R$, and then adding these polylines one by one. When adding a polyline, we find the leftmost point $X$ in the polyline that is not in the convex hull, and remove all points to the right of $X$ in the original convex hull. This way, we can sequentially insert all points of the polyline into the convex hull.

To determine if a line intersects the convex hull, we perform binary search to find the point with the closest slope to the query line and check the direction of the point relative to the query line.

Thus, we can complete the checking process by maintaining the convex hulls for the upper-left, upper-right, lower-left, and lower-right directions separately.

One more thing to note is that when both the query line segment and the polygon edge are perpendicular to the x-axis, neither of these line segments can be processed using divide-and-conquer. Therefore, we need to perform additional sorting and sweep line processing for these line segments.

Since each line segment is divided into $O(\log V)$ intervals, and the complexity bottleneck in each divide-and-conquer interval lies in sorting, the total time complexity is $O((n + q) \log (n + q) \log V)$.