自动搬运

查看原文

来自洛谷，原作者为

	wangsiyuanZP 蝴蝶飞过沧海，此行终抵群星

搬运于2025-08-24 23:06:43，当前版本为作者最后更新于2024-12-01 21:08:29，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

T1 做了超过一个半小时，还好有这道题让我逆天改命。

为什么都要什么容斥啊，感觉顺着做很自然啊，讲一下我的赛时简单做法。

$k=1$

我们已经知道是从那条边开始了，每一个点的过程就是从一条边来，以任意顺序，以一条链的形态走完自己后续的边，顺便访问自己子树的情况，答案就是：

这里 $0!=1$，$d_i$ 代表 $i$ 的度数。

朴素情况

接下来考虑 $k>1$ 的情况，显然从不同的边开始可能生成相同的树，我在考场里认为不可能进行容斥，遂有如下观察：

什么情况会生成相同的树？

考虑一个已经生成的新树，它可能由哪些根节点生成出来（后文中的根节点均指代“遍历起始边”）。

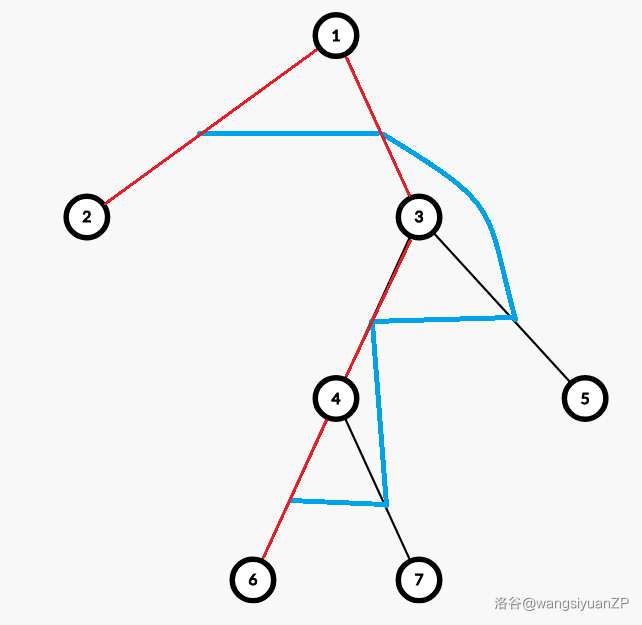
其中，蓝色边是新生成的树（对不起它是一条链，但是没有影响），红色边是可能作为根节点的原始边。

猜想：可能的根节点一定恰好是一条从原树的叶子到叶子的链。

证明也很简单，考虑一个点周围的所有黑边，这些边内部的蓝边一定是一条链，而只有链的两个端点可以作为根的方向。

一颗新树一定恰好有一条这样的链，所以我们可以根据链的形态来统计答案。

当链确定时，答案即为：

其中 $i$ 是所有节点，$v$ 是链上节点，这里认为 $0^{-1}=1$。

问题转化为：有一棵树，边有 $0/1$ 权值，点有点权，求所有叶子到叶子的链，满足这条链上有一条 $1$ 边，点权的乘积的和是多少。

这很简单，$n=2$ 特判一下，否则取一个非叶子节点当做根，dfs 一遍，记录每个节点的子树内，叶子到它有 $1$ / 没有一个 $1$ 的乘积总和 $sum_{u,0/1}$，计算对答案的贡献即可。

这是考完重写的代码，通过了民间数据，如有错误请指出。

// Calm down.
// Think TWICE, code ONCE.
#include<bits/stdc++.h>
#define pb push_back

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;

template<typename T> inline void read(T &x){
	x = 0; bool F = 0; char c = getchar();
	for (;!isdigit(c);c = getchar()) if (c == '-') F = 1;
	for (;isdigit(c);c = getchar()) x = x*10+(c^48);
	if (F) x = -x;
}

template<typename T1, typename... T2> inline void read(T1 &x, T2 &...y){read(x); read(y...);}

template<typename T> inline void checkmax(T &a, const T &b){if (a<b) a = b;}

template<typename T> inline void checkmin(T &a, const T &b){if (a>b) a = b;}

const int N = 1e5+5;
const ll MOD = 1e9+7;
int n, m, u[N], v[N], flag_edge[N], d[N];
vector<PII> to[N];
ll sum[N][2], inv[N], ans;

void dfs(int u, int fa){
	sum[u][0] = sum[u][1] = 0;
	int v;
	ll val = 0;
	for (auto x: to[u]){
		v = x.first; if (v == fa) continue;
		dfs(v, u);
		if (x.second) sum[v][1] += sum[v][0], sum[v][0] = 0;
		(val += sum[v][1]*(sum[u][0]+sum[u][1]) + sum[v][0]*sum[u][1]) %= MOD;
		(sum[u][0] += sum[v][0]) %= MOD;
		(sum[u][1] += sum[v][1]) %= MOD;
	}
	ll INV = inv[d[u]];
	(ans += val*INV) %= MOD;
	if (!d[u]) sum[u][0]++;
	(sum[u][0] *= INV) %= MOD;
	(sum[u][1] *= INV) %= MOD;
}

inline void solve(){
	read(n, m); for (int i = 1;i<=n;i++) d[i] = -1, to[i].clear(); ans = 0;
	for (int i = 1;i<n;i++) read(u[i], v[i]), flag_edge[i] = 0, d[u[i]]++, d[v[i]]++;
	int t; while (m--) read(t), flag_edge[t] = 1;
	if (n == 2){printf("1\n"); return;}
	for (int i = 1;i<n;i++) to[u[i]].pb({v[i], flag_edge[i]}), to[v[i]].pb({u[i], flag_edge[i]});
	int rt = 0; for (int i = 1;i<=n;i++) if (d[i]) rt = i;
	dfs(rt, 0);
	for (int i = 1;i<=n;i++){
		for (int j = 1;j<=d[i];j++) (ans *= j) %= MOD;
	}
	printf("%lld\n", ans);
}

int main(){
//	freopen("traverse.in", "r", stdin);
//	freopen("traverse.out", "w", stdout);
	inv[0] = inv[1] = 1; for (int i = 2;i<N;i++) inv[i] = inv[MOD%i]*(MOD-MOD/i)%MOD;
	int c, t; read(c, t); while (t--) solve();
	return 0;
}