自动搬运

查看原文

来自洛谷，原作者为

	allenchoi You are not alone.

搬运于2025-08-24 23:06:33，当前版本为作者最后更新于2025-03-07 08:59:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

科技：

Dijkstra，最短路树

思路：

首先，以 $1$ 号点为起点跑最短路，求出最短路树。
设操作的两条边编号为 $a,b(a<b)$，则 $b$ 是 $[a+1,m]$ 中边权最大的那条边。
假如 $a$ 不在树上 $1$ 到 $n$ 的路径上，此时的最短路就是原来的 $dis_{1,n}$；否则，最短路可能是 $dis_{1,n}+w_b$，也可能是经过一条非树边 $(x,y)$ 的路径，如下图：

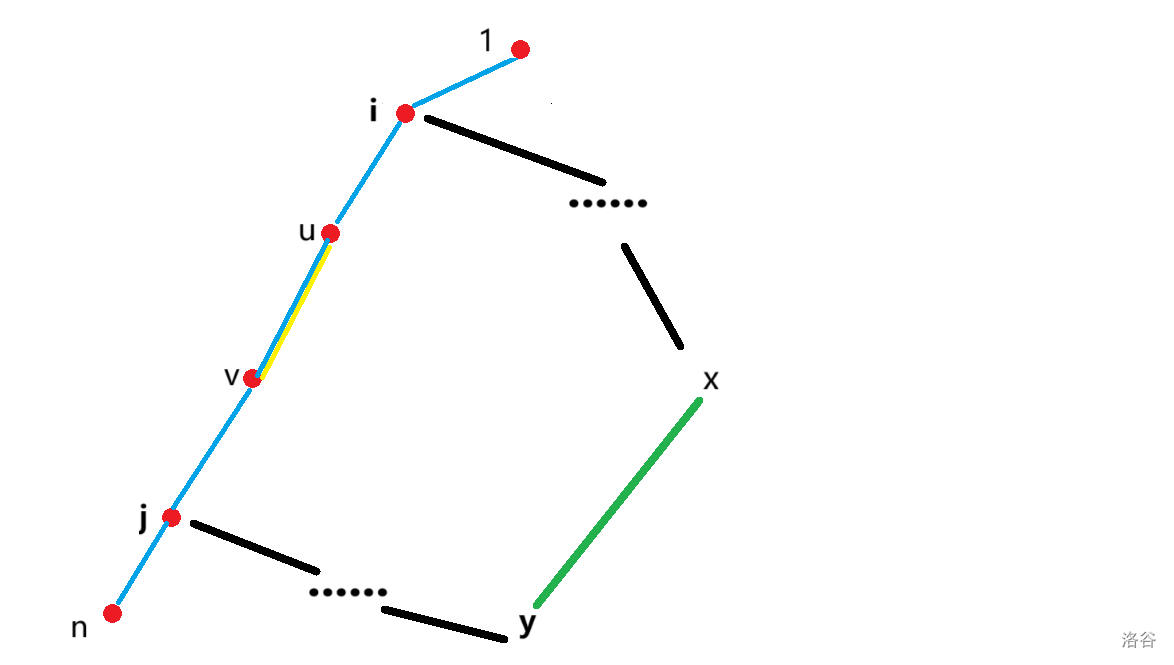
其中标黄的蓝边是 $a$ 边。
这种情况的最短路是 $dis_{1,x}+w_{x,y}+dis_{n,y}$，证明如下：
首先，由于点 $x$ 一定在 $u$ 的子树以外，所以 $1$ 到 $x$ 的最短路即树上路径必然不经过 $(u,v)$；
接下来考虑 $dis_{n,y}$ 对应的路径。
考虑反证法，假设该路径经过了 $(u,v)$，那么这条路径形如 $y,...u,v,...n$。注意到点 $y$ 是在 $v$ 的子树内的，所以 $v$ 是 $y$ 的祖先，那么 $y$ 到 $v$ 的最短路径就是树上的路径（考虑 Dijkstra 从 $v$ 到 $y$ 增广的过程），必然不经过点 $u$，因此比上面的那条路径更优。由此得出，$dis_{n,y}$ 对应的路径也不经过 $(u,v)$。
证毕。
考虑怎么计算答案。
我们称树上 $1$ 到 $n$ 的路径上的点为关键点，设 $x,y$ 最深的关键点祖先分别为 $i,j$（见上图），那么 $dis_{1,x}+w_{x,y}+dis_{n,y}$ 可以作为 $a$ 是 $i,j$ 之间的边时的答案。
于是可以离线处理。维护一个可重集，从上到下枚举关键点、关键边。枚举所有非树边 $(x,y)$，设它对应的最短路长度为 $v$，我们在 $i$ 的时候将 $v$ 加入 $s$，在 $j$ 的时候删除，那么一条关键边的答案就是 $\min(dis_{1,n}+w_b,\min\limits_{v\in s}v)$，最终答案就是这串东西的 $\max$。
我们只用跑两次最短路，做 $O(m)$ 次 multiset 操作，所以时间复杂度单 $\log$。
可能评个蓝或紫？

代码：

#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
const int N = 3e5 + 5;
const ll INF = 1e18;
int n,m,tot = 1,top,head[N],to[N << 1],val[N << 1],nxt[N << 1],vis[N << 1],w[N],p[N],id[N],h[N];
ll ans,dis[2][N];
vector <ll> v1[N],v2[N];
multiset <ll> s;
struct Node{int x,pre;ll d;};
bool operator < (Node x,Node y){return x.d > y.d;}
priority_queue <Node> q;
void add_(int x,int y,int z)
{
	to[++tot] = y,val[tot] = z;
	nxt[tot] = head[x],head[x] = tot;
}
void dijkstra(int s,int t)
{
	memset(dis[t],127,sizeof(dis[t]));
	dis[t][s] = 0,q.push((Node){s,0,0});
	while(!q.empty())
	{
		Node tmp = q.top();
		q.pop();
		int x = tmp.x,pre = tmp.pre;
		ll d = tmp.d;
		if(d > dis[t][x]) continue;
		vis[pre] = t;
		for(int i = head[x],y;i;i = nxt[i])
		{
			y = to[i];
			if(d + val[i] < dis[t][y])
			{
				dis[t][y] = d + val[i];
				q.push((Node){y,i,d + val[i]});
			}
		}
	}
}
bool dfs1(int x)
{
	p[++top] = x,h[x] = top;
	if(x == n) return true;
	for(int i = head[x],y;i;i = nxt[i])
	{
		y = to[i];
		if(!vis[i]) continue;
		id[top] = i / 2;
		if(dfs1(y)) return true;
	}
	top--,h[x] = 0;
	return false;
}
void dfs2(int x)
{
	for(int i = head[x],y;i;i = nxt[i])
	{
		y = to[i];
		if(!vis[i]) continue;
		if(!h[y]) h[y] = h[x];
		dfs2(y);
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1,a,b,c;i <= m;i++)
	{
		scanf("%d%d%d",&a,&b,&c);
		add_(a,b,c),add_(b,a,c);
		w[i] = c;
	}
	for(int i = m;i >= 1;i--) w[i] = max(w[i],w[i + 1]);
	dijkstra(n,0),dijkstra(1,1);
	dfs1(1),dfs2(1);
	for(int i = 1;i <= n;i++)
		for(int j = head[i];j;j = nxt[j])
			if(!vis[j] && h[i] < h[to[j]])
			{
				ll tmp = dis[1][i] + dis[0][to[j]] + val[j];
				v1[h[i]].pb(tmp),v2[h[to[j]]].pb(tmp);
			}
	for(int i = 1;i < top;i++)
	{
		for(ll v : v1[i]) s.insert(v);
		for(ll v : v2[i]) s.erase(s.lower_bound(v));
		ans = max(ans,min(dis[1][n] + w[id[i] + 1],s.empty() ? INF : (*s.begin())));
	}
	printf("%lld\n",ans);
	return 0;
}