自动搬运

查看原文

来自洛谷，原作者为

	Mathison **

搬运于2025-08-24 21:21:19，当前版本为作者最后更新于2018-09-29 18:55:33，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意让我们用最少的代价把叶子节点到根节点的距离调成相同

显然，我们调整靠近根节点的树枝，其下叶子节点距离根节点的距离都会增加，所以，调整越靠根节点的树枝调整的代价越少。

为了方便作图，效果直观，在此我们用节点深度类比距离

所以我们可以先找到最深的叶子节点

再从最小的子树开始，把所有子节点调整到同一深度，再调整子树上面的树枝

理解不了的话看这个图：

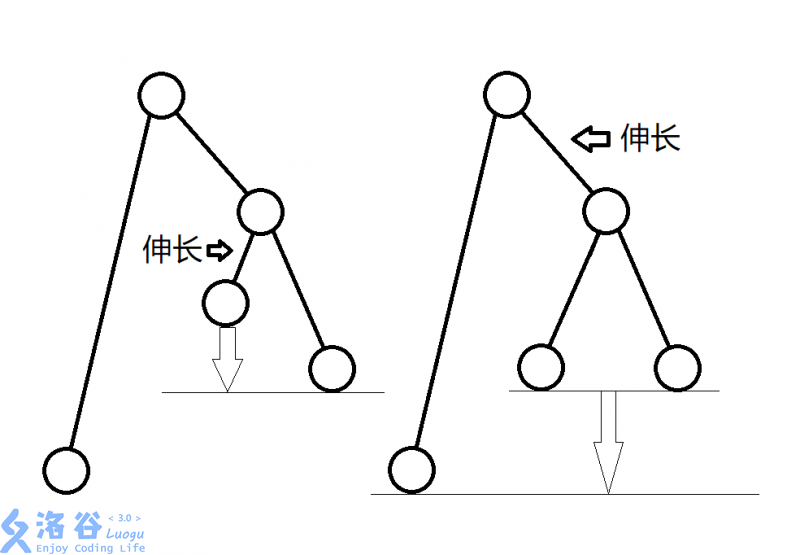
这样我们就可以保证用最少的代价把所有叶子节点调整到同一深度

我们理解了这个问题就可以设计dfs了

每次调整的代价都是$dis[x]-(dis[ver[i]+edge[i])$

把它累加即可

下面是详细代码

#include<bits/stdc++.h>
using namespace std;
const int N=500010;
int head[N],ver[N],next[N],tot,n,st,edge[N];
long long ans,dis[N];
void add(int x,int y,int z)//建图
{
	ver[++tot]=y;
	edge[tot]=z;
	next[tot]=head[x];
	head[x]=tot;
} 
void dfs(int x,int fa)
{
	for(int i=head[x];i;i=next[i])
	{
		int y=ver[i],z=edge[i];
		if(y==fa) continue;
		dfs(y,x);//继续搜子树
		dis[x]=max(dis[x],dis[y]+z);更新这棵子树根节点和叶子节点的最大距离
	}
	for(int i=head[x];i;i=next[i])
	{
		int y=ver[i],z=edge[i];
		if(y==fa) continue;
		ans+=dis[x]-(dis[y]+z);//累加每次调整的代价
	}
}
int main()
{
	scanf("%d%d",&n,&st);
	for(int i=1;i<n;i++)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);add(y,x,z);//注意双向边
	}
	dfs(st,0);
	printf("%lld",ans);
	return 0;
}