1 条题解
-
0
自动搬运
来自洛谷,原作者为

yyyhy
NJU,赢!|2021年√7但NOIP两年没奖两年省二的被单调队列的拿不到省一的蒟蒻准大一牲|GD-MM|即将JS-NJ|male|主页U549373|被取关了取关随意qwq搬运于
2025-08-24 23:05:59,当前版本为作者最后更新于2024-11-15 17:36:52,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
本题解目前提供 hash,kmp 和 SA 做法。
Updated on 2024·12·1 增加 kmp 做法,更正样例。
Updated on 2025·7·13 修复挂掉的云剪贴板。一、分析
推结论
首先进行题意分析,题目要求最短的 ,直接枚举 肯定是不现实的,所以要对 进行处理。
所以我们来分析样例:
qwq→qwqwq
lingyu→lingyulingyu
aaaaaaabaa→aaaaaaabaaaaaaabaa发现两个样例中间都有重复的部分,所以我们用括号标出中间用了两次的部分,如下:
qwq→qw(q)wq
lingyu→lingyu()lingyu
aaaaaaabaa→aaaaaaab(aa)aaaaabaa不难发现,括出来的部分是 的最长 border,也就是求一个最长的串 (可以为空)使 既是 的前缀,又是 的后缀,且不为 ,这样这个 就可以用两次。(这个是后面说的假设)
即为 。二、证明
1. 证明 是 的 border
因为 为 的前缀,所以可令 ,于是 ,满足 是 的前缀。
又因为 为 的后缀,所以可令 ,于是 ,满足 是 的后缀。
所以 是 的 border。
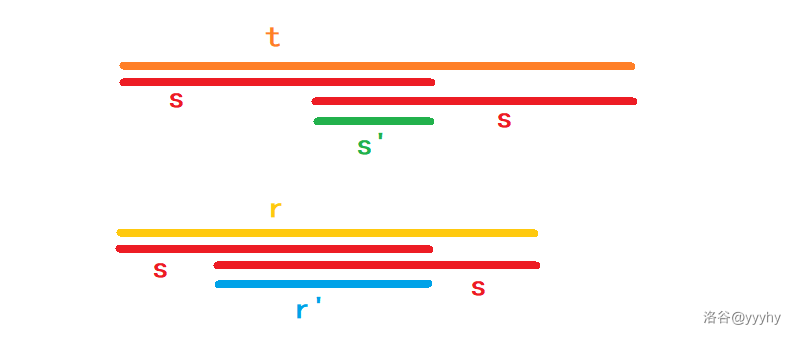
2. 证明 是满足条件的最短的
如果有比 更短的 满足条件,设中间用两次的部分为 ,那么 会长于 ,且 既是 的前缀,又是 的后缀,如图,与假设矛盾。
3. 证明 是 最长的 border
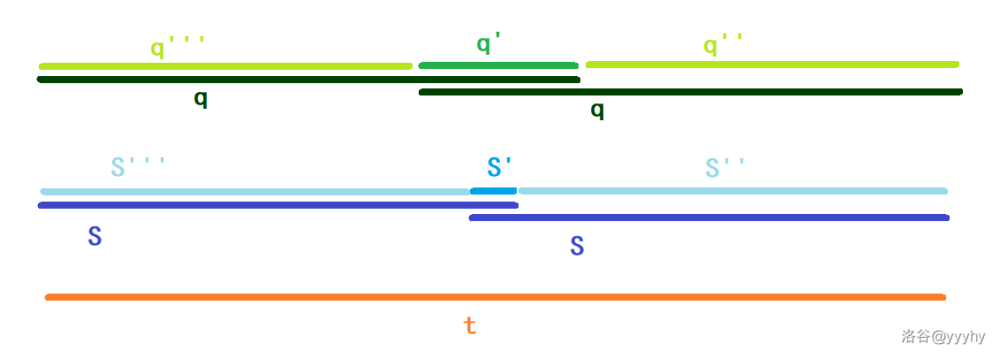
若存在更长的 是 的 border,那么可令 。
于是如图:
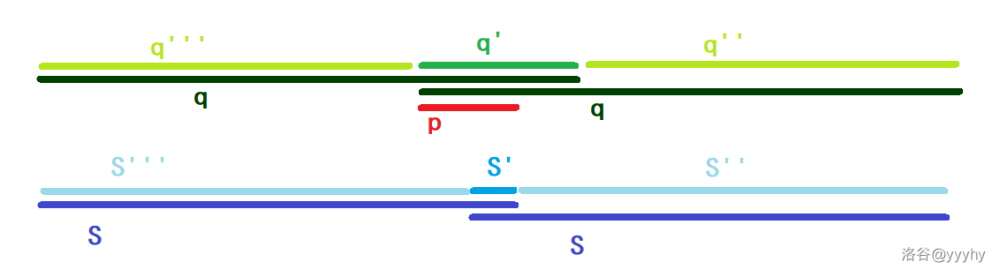
然后记 左端点到 右端点这一段为 ,那么如下图推断:
通过 转换位置:
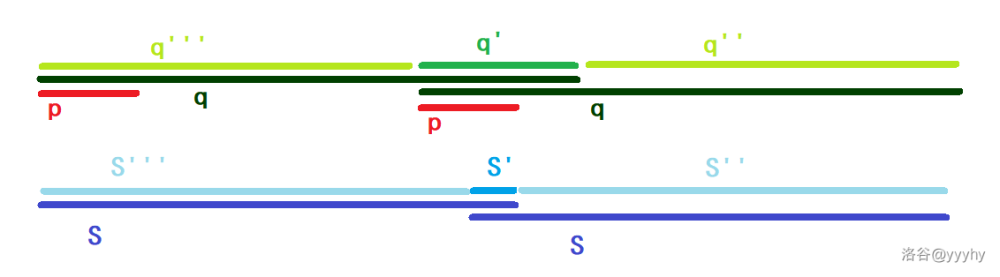
于是我们发现 既为 前缀,又为 后缀,且长于 ,这与假设矛盾,不成立。
所以 是 最长的 border。
所以现在问题就变成了求 的最长 border,即 。
三、解决问题
首先,我们会想到枚举,即从 到 枚举 ,复杂度 ,加特殊性质可以干到 57pts,数据加强前实际 100pts,当然,现在
骗不过了。然后我们想优化:
字符串哈希
据说这是这道题黄题的原因,但我太蒟了,不会。
终于学会 hash 了!——2024·11·16
hash 做法(11·16补充)
其实这个比较好实现,就是算出长度为 的前缀和后缀的 hash,从 开始(因为不能 )枚举到 ,有 hash 相等就记录跳出,最后输出。
但是众所周知,hash 非常好卡,所以为了保险我们用双 hash。
但是众所周知,双 hash 也能卡,所以为了追求 正确率,最好加一层判断,从大到小判断每一对双 hash 都相等的前后缀是否真的一样,一样就跳出循环,也就是写一个无错双 hash。
这都卡那我就 T 罢(悲于是取两个比较大的质数 和 ,也就是代码中的 和 ,进行 hash 操作,我取了 和 ,因为有乘法,所以要开
long long。hash 的计算比较简单就不介绍了,看代码应该看得懂。
其中:
指 情况下的前 位 hash,
指 情况下的后 位 hash,
指 情况下的前 位 hash,
指 情况下的后 位 hash。hash 代码,复杂度极大概率是 ,卡死(应该做不到)。
这个比 SA 快多了,最慢 32ms。
KMP/AC 自动机
没学过,也不会。(wtcl/kk)
学会了,但是 AC 自动机跟 kmp 没啥区别,不打了,打一个 kmp 做法。——2024·12·1
前文已经证明问题就是求 的最长 border,也就是求出 就可以了,不会的这里有板子,剩下的就简单了。
kmp 代码,这个速度最快,最慢 16ms。
于是我开始尝试用考场的第一反应:
SA(后缀数组)
这玩意我就不多介绍了,板子题解里讲的非常详细。
但是板子题的题解也说了,光求后缀数组一般是没用的,还要求一个东西,就是每个后缀和后缀数组中排序相邻的后缀的最大公共前缀长。
先求再说:
for (int i = 1, h = 0; i <= n; i++) { if (h) h--; int j = sa[rk[i] + 1]; while (i + h <= n && s[i + h] == s[j + h]) h++; sam[rk[i]] = h; }解释一下:
定义 为 开始的后缀与 开始的后缀的最大公共前缀长。
本来每两个后缀数组中相邻的后缀分别枚举会到 ,但有一个特殊性质可以帮我们优化复杂度:
假设 ,那么 。reason:假设 开始的后缀和 开始的后缀最大公共前缀长为 ,那么 开始的和 开始的最大公共前缀长至少为 ,故 。
这样由于 不能超过 且最多被减 次 。
所以复杂度 ,不会 T。那么我们知道了这个有什么用呢?
我们就可以求所有后缀中最长的,且满足是 前缀的后缀了。
接下来的思路:
在 中从 倒序枚举到 ,分别看每个后缀和 最大公共前缀长是不是等于从这个位置开始的后缀长,等于则记录跳出,这个最大公共前缀长即为 。因为最大公共前缀长只减不增,所以最先枚举到的就是最长的。
一个说明:为什么向前枚举就行了?
因为 是 的前缀,根据后缀数组的排序, 作为后缀时的排序位置一定在 位置的前面。代码如下:
int minl = inf, maxl = 0, nowwh = rk[1] - 1; while (nowwh) { minl = std :: min(minl, sam[nowwh]); if (minl == n - sa[nowwh] + 1) { maxl = minl; break; } nowwh--; }最后输出即可。
完整代码在这里,复杂度 ,
虽然做出来了但是好慢,最慢要 712ms。
- 1
信息
- ID
- 10910
- 时间
- 2000ms
- 内存
- 512MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
