自动搬运

查看原文

来自洛谷，原作者为

	Twlight！ 追求真理之人不可心存傲慢，不可嘲笑无法用科学解释的奇迹，不可回避这个世界的美丽。

搬运于2025-08-24 23:05:52，当前版本为作者最后更新于2024-11-08 10:39:28，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

andychen打球时直接想出半平面交做法这我哪会写啊。

初步思路（半平面交）

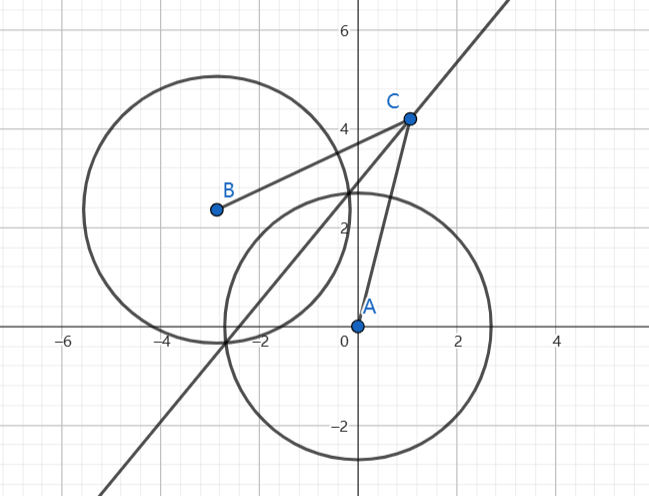
观察到警察与劫匪都只能走一条射线，且相同时间内他们行驶的路程都一样，那么不难发现劫匪被某个警察抓住时，抓住的位置在劫匪与那个警察连线的中垂线上，如图。

显然劫匪无法穿过这条中垂线，否则必会被警察抓到。换句话说，每个警察与劫匪的连线的中垂线都限制了劫匪的活动范围，这些半平面或交成了个凸多边形。不难发现我们要求出劫匪最远能跑的距离，就相当于求这个凸多边形的顶点与原点的距离的最大值。

判断劫匪永远都不会被抓到也很简单，看半平面交围成的是否是一个有范围的凸多边形即可。

时间复杂度 $O(n \log n)$。

简化难度（二分答案）

我不会半平面交，只能换一种思路进行解决了。

发现答案是具有单调性的，考虑二分答案。此时问题就变为了，判断劫匪是否能跑 $\text{mid}$ 距离，即劫匪是否能到达以原点为圆心，$\text{mid}$ 为半径的圆的圆弧上。

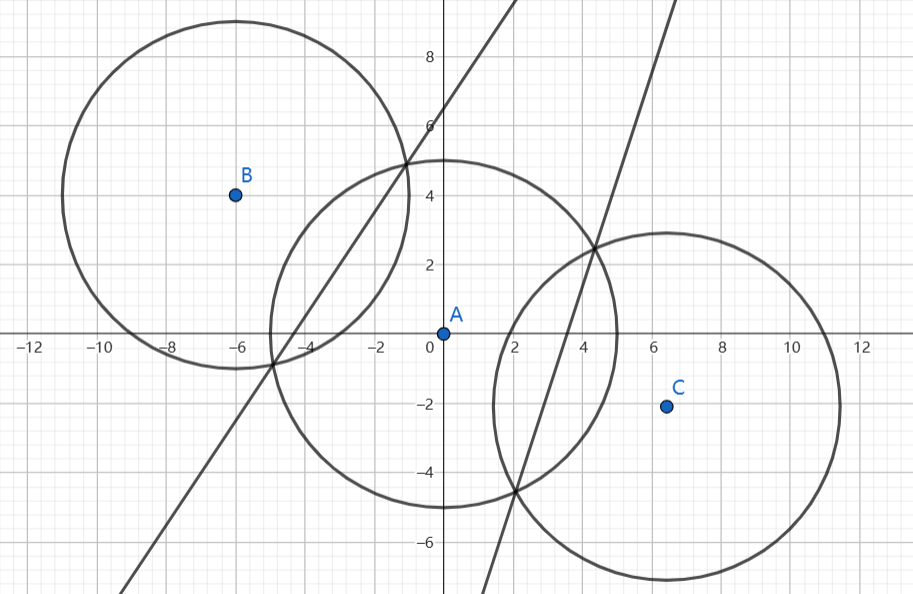
我们把每个警察也看成大小为 $\text{mid}$ 的圆，显然警察的圆与劫匪的圆的交点，在警察与劫匪的连线的中垂线上，如图。

显然劫匪不能越过中垂线，而劫匪又只能在圆弧上移动，可以发现每个警察或覆盖了圆弧的一部分，或没有覆盖。如果存在一个点，那个点没有被任何警察覆盖，那么劫匪就一定可以跑到那里（弦围成的多边形是凸的），用朴素方法判断线段覆盖就可以了。

做法也比较简单，把交点转为方位角之类的角度，变为一段区间，最后排个序判断是否全覆盖即可。至于求交点一事，可查阅相关代码或推式子。

这里再提一嘴二分上界，我认为这可能是考场上最难发现的问题。两条中垂线的交点，可能到达 $10^9$ 的级别，因为两条直线可能斜率都很极端，导致最终的交点非常远，如果不注意就可能爆零。

时间复杂度 $O(n \log^2 n)$，虽然慢了但是应该比较好写。

参考代码

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int ll
#define double long double

const int N = 100000 + 10;
const double inf = 1e10;
const double PI = acos(-1);
const double eps1 = 1e-18;
const double eps2 = 1e-6;

using namespace std;

int read () {
	int x = 0, k = 1;
	char c = getchar();
	while (c < '0' || c > '9') { if (c == '-') k = -1; c = getchar(); }
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
	return (1ll * x * k);
}

using Pdd = pair<double, double>;
using Pdi = pair<double, int>;

int n;
Pdd P[N], P0(0, 0);

double sqr (double x) { return x * x; }
double sgn (double x, double eps = eps1) { return x < -eps ? -1 : x > eps; }

vector<double> findPoint (Pdd A, Pdd B, double r) {
	vector<double> ret; double d = sqrt(sqr(A.first - B.first) + sqr(A.second - B.second));
	if (!sgn(d) || d - 2 * r >= eps1) return ret;
	double q = atan2(B.second - A.second, B.first - A.first), h = acos(d / r / 2);
	double a1 = q - h, a2 = q + h;
	if (a1 < eps1) a1 += 2 * PI; if (a2 < eps1) a2 += 2 * PI;
	ret.push_back(a1), ret.push_back(a2); return ret;
}

bool check (double r) {
	vector<Pdi> Arg; int cnt = 0;
	for (int i = 1; i <= n; ++i) {
		auto q = findPoint(P0, P[i], r);
		if (!q.size()) continue;
		Arg.emplace_back(q[0], 1);
		Arg.emplace_back(q[1], -1);
		cnt += (q[0] - q[1] > eps1);
	}

	if (!cnt) return 1;

	sort(Arg.begin(), Arg.end(), [](Pdi A, Pdi B){ return A.first - B.first < eps1; }); 

	for (int i = 0, l = Arg.size(); i < l; ++i) {
		cnt += Arg[i].second;
		if (!cnt) return 1;
	}
	return 0;
}

signed main() {
	n = read();
	for (int i = 1, X, Y; i <= n; ++i) X = read(), Y = read(), P[i] = Pdd(X, Y);

	if (check(inf)) puts("-1"), exit(0);

	double l = 0, r = inf, mid;
	while (r - l > eps2) {
		mid = (l + r) / 2;
		if (check(mid)) l = mid;
		else r = mid;
	}
	printf("%.10Lf\n", r); 

	return 0;
}