自动搬运

查看原文

来自洛谷，原作者为

	ppllxx_9G One plus one does not equal two

搬运于2025-08-24 23:05:40，当前版本为作者最后更新于2024-11-03 16:16:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

也许更烂的阅读体验

题意

是否存在一个由 $n$ 个 $0$ 和 $m$ 个 $1$ 组成的串，满足任意一个长度为 $[2L,2R]$ 的子串中 $n$ 和 $m$ 的个数不相等。

转化

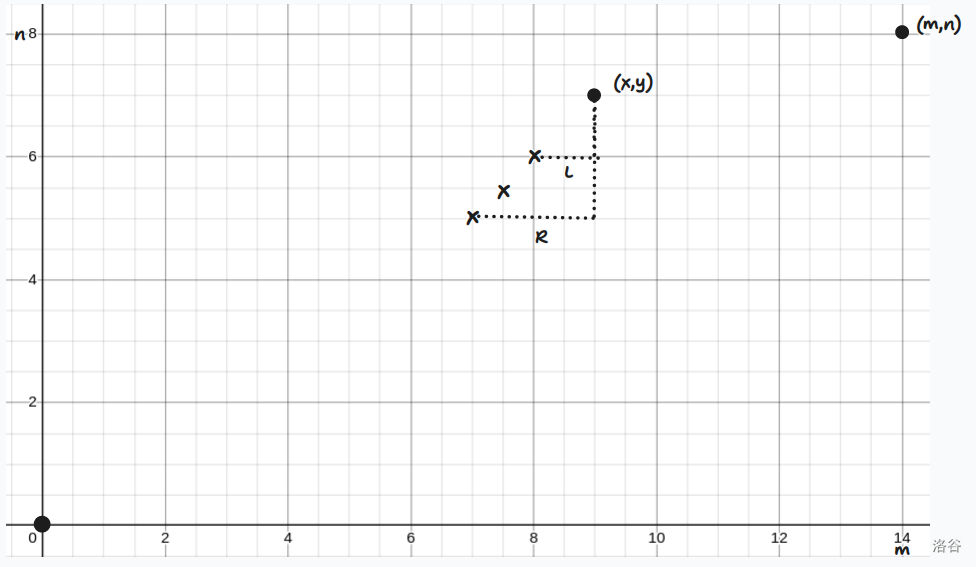
对于 01 串个数相等的问题，容易想到将其转化为在二维平面中走网格的问题，即每选择一个 $1$ 相当于向下走一格，选择一个 $0$ 相当于向左走一格。

这样的话，一个子串内 $0$ 和 $1$ 的个数相同可以表示为同时选择了 $(x,y)$ 和 $(x-k,y-k)$ 两个点，$k$ 表示区间长度。

我们就成功将题意转化成了：从 $(m,n)$ 向左或向下走，走到 $(0,0)$，每走过一个点会产生几个不可走的位置，问是否存在一条路径，使其不经过不可走位置。

贪心

然后你发现就做完了。

这个问题看起来就很可做，我们先考虑最优的走法是什么？

显然最开始在 $(n,m)$ 的时候，会在斜下方有 $R-L$ 个点不可走，这些不可走的点和当前走到的位置的相对位置是固定的，也就是我们怎么移动当前点，那一串不可走的位置就会跟着平移。

草率的想一下，如果某一时刻我们走到了 $(x,y)$，最近的不可走点 $(x-L,y-L)$ 已经在数轴下面了（某一维小于零），那我们就可以任意走了。所以不如让 $n$ 作为较小的，然后钦定一开始向下走（方便下面说）。

延续上面的思路，我们尽量让不可走位置先进入数轴下面，直接贪心。先走到 $(m-L-1,n-L+1)$，然后贴着不可走位置走。最后能走到就能，不能就不能。

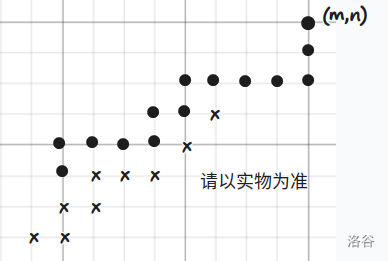
建议考虑不可走位置的边界（挨着圆点的小叉），如果最后与 x 轴的交点大于零，那就可以。

发现不可走位置会跟着路径平移，也就是不可走位置的边界会复制我们走的路径，路径又需要贴着边界走，就是一个类似螺旋升天分形的过程。建议从 $L=R$ 的情况开始考虑，这时只有一个点，容易发现边界是有规律的，即每向下 $L-1$ 步，向左 $L+1$ 步为一个周期，然后你就会做了。

推广到 $R = L+1$ 的情况，发现就是在 $R = L$ 的边界上多了几个凸点，周期和步长不变。考虑 $R-L$ 会对边界有什么影响。第一次会在一条笔直向下的边界上多 $R-L$ 个凸点，由于是类似分形的结构，后面每一个周期都会多 $R-L$ 个凸点，直到边界变成阶梯状。

现在你闭着眼都知道边界是什么样的了，计算周期，小心处理最后接近 x 轴的一小段，你就做完了。

注意一些 Corner case。

附上打表器。

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e4+5;
LL n,m,l,r;
char a[N][N];

int main()
{
	// freopen("in.in","r",stdin);
	// freopen("out.out","w",stdout);
	int T; scanf("%d",&T);
	while(T--)
	{
		scanf("%lld%lld%lld%lld",&l,&r,&n,&m);
		if(n>m) swap(n,m);
		for(int i=0;i<=n;i++)
			for(int j=0;j<=m;j++) a[i][j]='c';
		// if(n==0||m==0) puts("Yes");
		queue<pair<LL,LL> > q;
		q.push({n,m});
		while(!q.empty())
		{
			LL x=q.front().first,y=q.front().second; q.pop();
			a[x][y]='a';
			for(int i=l;i<=r;i++)
			{
				if(x-i<0||y-i<0) break;
				a[x-i][y-i]='b';
			}
			if(x-1>=0&&a[x-1][y]!='b'&&(!(y>=m-l&&x==n-l+1))) q.push({x-1,y});
			else if(y-1>=0&&a[x][y-1]!='b') q.push({x,y-1});
		}
		if(a[0][0]=='a') puts("Yes");
		else puts("No");
		for(int i=n;i>=0;i--)
		{
			for(int j=0;j<=m;j++) printf("%c ",a[i][j]); putchar('\n');
		}
		putchar('\n');
	}
	return 0;
}

AC record