1 条题解
-
0
自动搬运
来自洛谷,原作者为

Zaunese
问题不在于自我有限,而在于自我设限。搬运于
2025-08-24 23:05:35,当前版本为作者最后更新于2025-01-11 11:39:20,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
考虑 怎么做。
转化成选若干个点,任意点间距离至少为 ,点权和最大。
考虑 DP:考虑了 ,点权和最大为 ,有单步转移 。 的左右两边分别表示选或不选 。初值 。
考虑优化转移。
如果只考虑“选”,可以考虑把模 相同的 放到数列的同一位置上(即原地化),一次转移只要给所有位置加上对应的 。这可以用离散化、线段树轻松完成。
考虑“不选”。感觉不是很好做,于是变单步转移为断点转移。具体地,改写 的定义为考虑到了前 个点,其中第 个必须选。转移为 。
延续模 分类、除 分层的思路。向 转移的过程可以表示为下图。
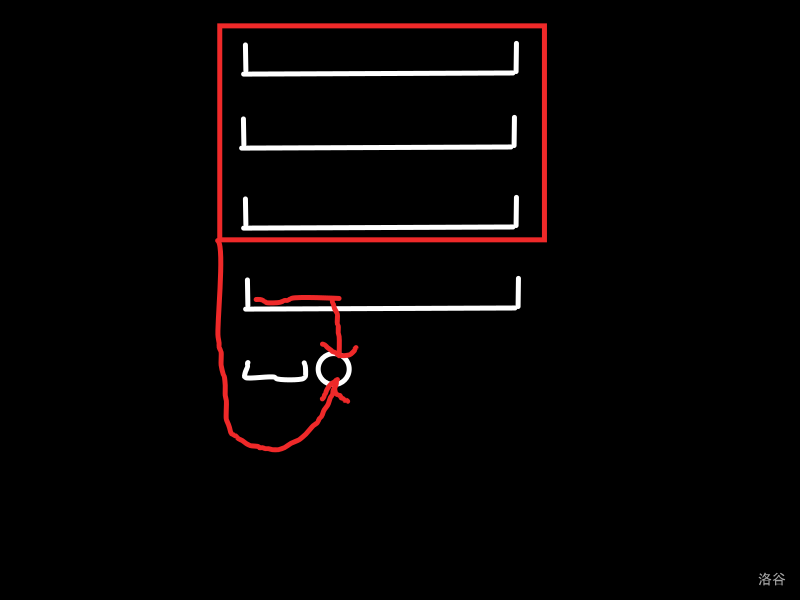
圆圈表示 ,红线部分是 。
具体地,要转移的就是上上层及以前的全局 ,和上层的前缀 ,更新到 。
一整层转移完 后,给所有位置加上对应的 。
可以轻松地发现,离散化之后,只要在每个 区间的左端点处存 DP 值,否则答案上可能不优。
直接做大约是 的,这是因为有的区间可能太长,此时转移方程中的 必然取 ,只要算一下 加了多少次就行了。
时间复杂度 。
大概是一份 QOJ 上可过的代码。
#include<cstdio> #include<cstring> #include<algorithm> #include"jumpgame.h" #include<tuple> #define fi first #define se second #define mkp std::make_pair using ll=long long; using std::min; using std::max; template<class T> void cmax(T&a,T b){a=max(a,b);} template<class T> void cmin(T&a,T b){a=min(a,b);} ll play_game(ll N, int Q, ll K, std::vector<ll> L, std::vector<ll> R){ const ll INF=ll(1e18)+100; std::vector<ll> tad(Q*4+5),trs(Q*4+5); std::vector<ll> dic; auto doadd=[&](int x,ll z){ trs[x]+=z; tad[x]+=z; }; auto dn=[&](int x){ if(tad[x]){ doadd(x*2,tad[x]); doadd(x*2+1,tad[x]); tad[x]=0; } }; auto add=[&](auto&&self,int x,int l,int r,ll ql,ll qr,ll z)->void{ if(qr<dic[l]||dic[r]<ql) return; if(ql<=dic[l]&&dic[r]<=qr) doadd(x,z); else{ int mid=l+r>>1; dn(x); self(self,x*2,l,mid,ql,qr,z); self(self,x*2+1,mid+1,r,ql,qr,z); trs[x]=max(trs[x*2],trs[x*2+1]); } }; auto upd=[&](auto&&self,int x,int l,int r,ll p,ll z)->void{ if(p<dic[l]||dic[r]<p) return; if(l==r) cmax(trs[x],z); else{ int mid=l+r>>1; dn(x); self(self,x*2,l,mid,p,z); self(self,x*2+1,mid+1,r,p,z); trs[x]=max(trs[x*2],trs[x*2+1]); } }; auto que=[&](auto&&self,int x,int l,int r,ll ql,ll qr)->ll{ if(qr<dic[l]||dic[r]<ql) return 0; if(ql<=dic[l]&&dic[r]<=qr) return trs[x]; else{ int mid=l+r>>1; dn(x); return max(self(self,x*2,l,mid,ql,qr), self(self,x*2+1,mid+1,r,ql,qr)); } }; auto build=[&](auto&&self,int x,int l,int r)->void{ if(l==r){ trs[x]=l?-INF:0; }else{ int mid=l+r>>1; self(self,x*2,l,mid); self(self,x*2+1,mid+1,r); trs[x]=max(trs[x*2],trs[x*2+1]); } }; auto dfs=[&](auto&&self,int x,int l,int r)->void{ printf("%d[%d,%d]%lld\n",x,l,r,trs[x]); if(l!=r){ int mid=l+r>>1; dn(x); self(self,x*2,l,mid); self(self,x*2+1,mid+1,r); } }; std::vector<std::pair<ll,int> > v; dic.push_back(-1); for(int i=0;i<Q;++i){ dic.push_back(L[i]%K); v.emplace_back(L[i],1); v.emplace_back(R[i]+1,-1); } std::sort(dic.begin(),dic.end()); dic.erase(std::unique(dic.begin(),dic.end()),dic.end()); build(build,1,0,dic.size()-1); std::sort(v.begin(),v.end()); ll sum=0,last=-1; for(int i=0;i<(int)v.size();){ ll b=v[i].fi/K; if(b-last>1){ upd(upd,1,0,dic.size()-1,-1,trs[1]+(b-last-2)*sum); add(add,1,0,dic.size()-1,0,K,(b-last-1)*sum); } ll l=0,x=trs[1]; int j=i; std::vector<std::tuple<ll,ll,ll> > upds; for(;j<(int)v.size()&&v[j].fi/K==b;++j){ upds.emplace_back(l,v[j].fi%K-1,sum); if(v[j].se>0){ upd(upd,1,0,dic.size()-1,v[j].fi%K, que(que,1,0,dic.size()-1,-1,v[j].fi%K)); } sum+=v[j].se; l=v[j].fi%K; } upds.emplace_back(l,K-1,sum); upd(upd,1,0,dic.size()-1,-1,x); last=v[i].fi/K; for(auto p:upds){ ll l,r,x; std::tie(l,r,x)=p; add(add,1,0,dic.size()-1,l,r,x); } i=j; } fprintf(stderr,"%d\n",1); return trs[1]; }
- 1
信息
- ID
- 10942
- 时间
- 3000ms
- 内存
- 1000MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
