自动搬运

查看原文

来自洛谷，原作者为

	Mutsumi_0114 **

搬运于2025-08-24 21:21:13，当前版本为作者最后更新于2018-12-13 09:20:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

算法：树形$dp$。 分析如下

先看样例这棵树，

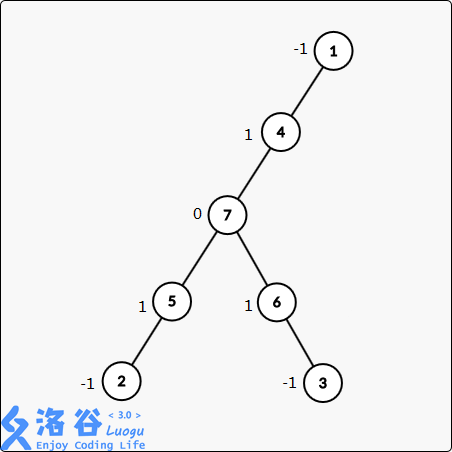
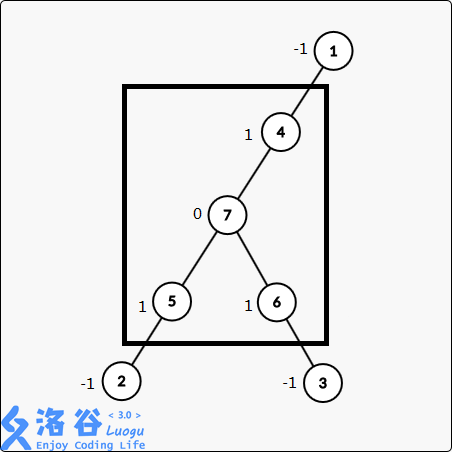
题意是要我们找到树上点权之和最大的一个连通分量，譬如满足样例的选择就是下图中框起来的一块，

我们用 $f[i]$ 记录 以$i$为根的子树中点权和最大的一棵子树（或只选根），$a[i]$ 是输入的点权。

因为这样做的话最后要从每个$f[i]$中找出最大的数作为答案输出，所以 选择哪个点为根对结果没有影响，毕竟 任一连通分量在任一时刻总是可以看成一棵以某个点为根的树。

那不妨设节点 $1$ 为根，点 $0$ 为它的父亲（图中没有标出点 $0$）。

接下来我们看看 $f[i]$ 如何计算。

根据定义，在走到点 $u$ 时，$f[u]$ 所表示的连通分量中必包含点 $u$ ，所以把 $f[u]$ 初始化为点 $u$ 的点权 $a[u]$。

接下来，对于 $u$ 的每一棵子树，我们都可以选择剪枝或不剪枝。对于 $u$ 的一个儿子 $v$ ，显然当 $f[v] < 0$ 时就剪断 $u-v$ 这条枝，反之。

于是得出递推式：

$f[u] = a[u] + (f[v] > 0 ? f[v] : 0)$ （$v$ 为 $u$ 的儿子）。

比如上图中，$f[2] = a[2] = -1$。

$∵ f[2] < 0$

$∴ f[5] = a[5] + 0 = 1$。

实现比较简单：

#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int n,a[16005],f[16005],ans=-2147483647;
vector <int> E[16005];
void dfs(int u,int fa)
{
    f[u]=a[u];//f初始值
    for(int i=0;i<E[u].size();i++)
    {
        int t=E[u][i];
        if(t!=fa)
        {
            dfs(t,u);
            if(f[t]>0)
                f[u]+=f[t];//如式
        }
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);//点权输入
    for(int i=1;i<n;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        E[u].push_back(v);
        E[v].push_back(u);//vector双向连边
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
        ans=max(ans,f[i]);//找出最大点权和
    printf("%d",ans);
    return 0;
}