1 条题解
-
0
自动搬运
来自洛谷,原作者为

Solwek
比唐挑战吗,那我赢了搬运于
2025-08-24 23:05:18,当前版本为作者最后更新于2024-10-20 08:23:02,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题意:
给定长度为 的序列 。
一共 次询问,每次询问给定 ,你需要输出有多少 满足 。
题解:
对于异或问题,考虑字典树。
我们把关于 和 的 放到字典树上,考虑 在什么情况下会使得满足条件。
从高到低枚举位,
- 前 位都一样,并且第 位的 是
我们发现只要 与 异或值为 便一定满足条件,那么可以对这个节点打一个 的标记,只要询问的 经过这里,那么就一定会产生这个贡献,并且已经不用再往下深入了,因为只要到了这个点就有贡献,与子树无关。
但是还要考虑如果这位的 与 异或也为 的话那么就还需要继续考虑后面的位数,继续去看其他的节点是否可行。
- 前 位都一样,并且第 位的 位是
那么此时只有当异或值位 时才有可能能产生贡献,而异或值为 时则一定不行,所以只需要考虑 的情况即可。
并且我们需要对最后移位特判,因为等于这种情况也是可行的。
对于查询只需要按照 的二进制从上往下走一遍将打的标记加起来就行了。
当 和 时举个例子。
-
对于最高位,只有 这位等于 才可能产生贡献,所以只建立一个 的节点。
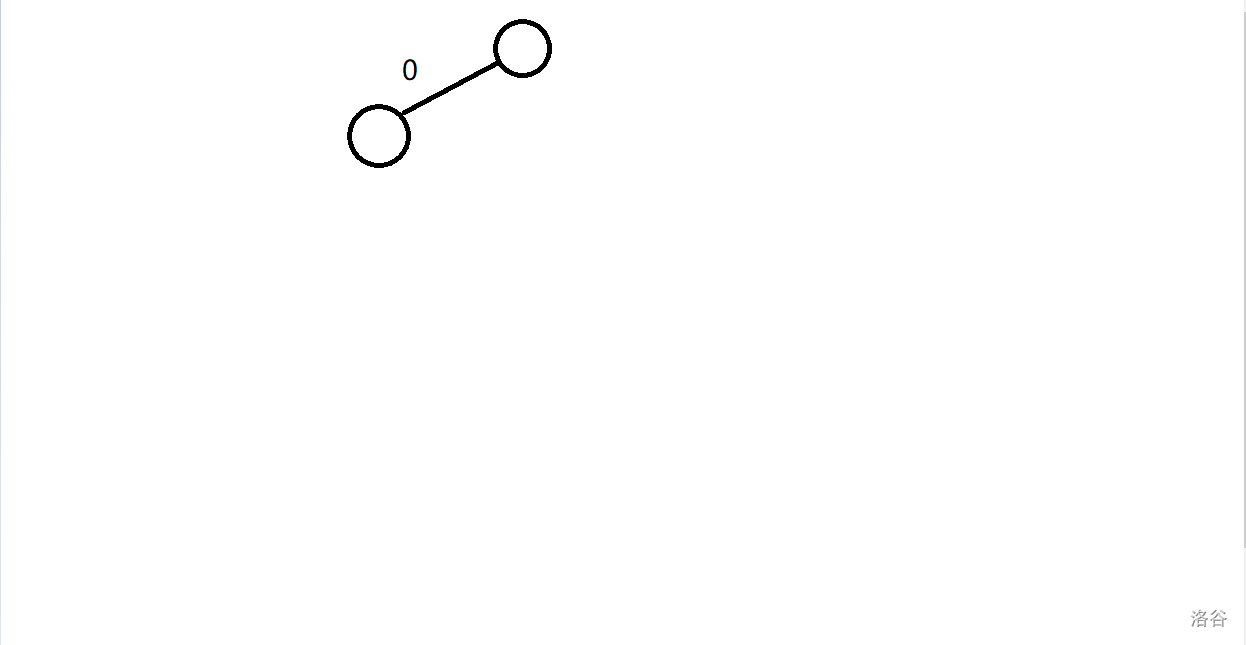
-
对于第二位,当 这位等于 时一定可行,所以在 那里 。当 这位等于 时也可能可行,所以也要建立一个节点。
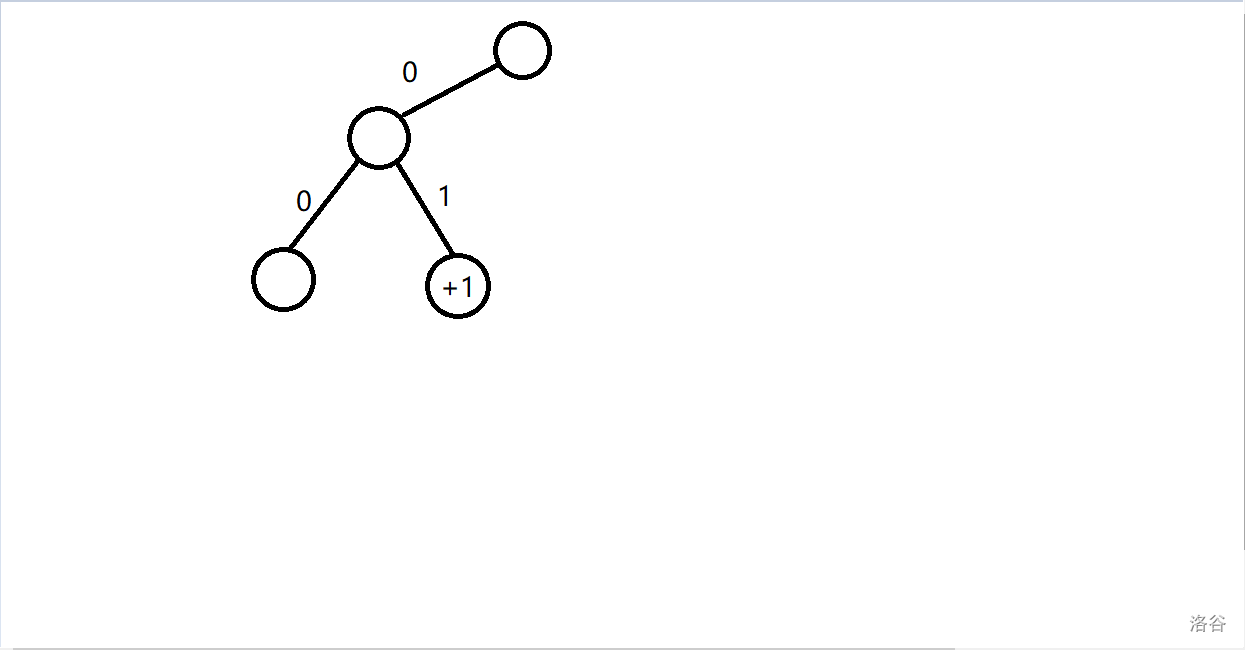
-
对于第三位,只有 这位等于 时可能可行,所以往 建立节点。
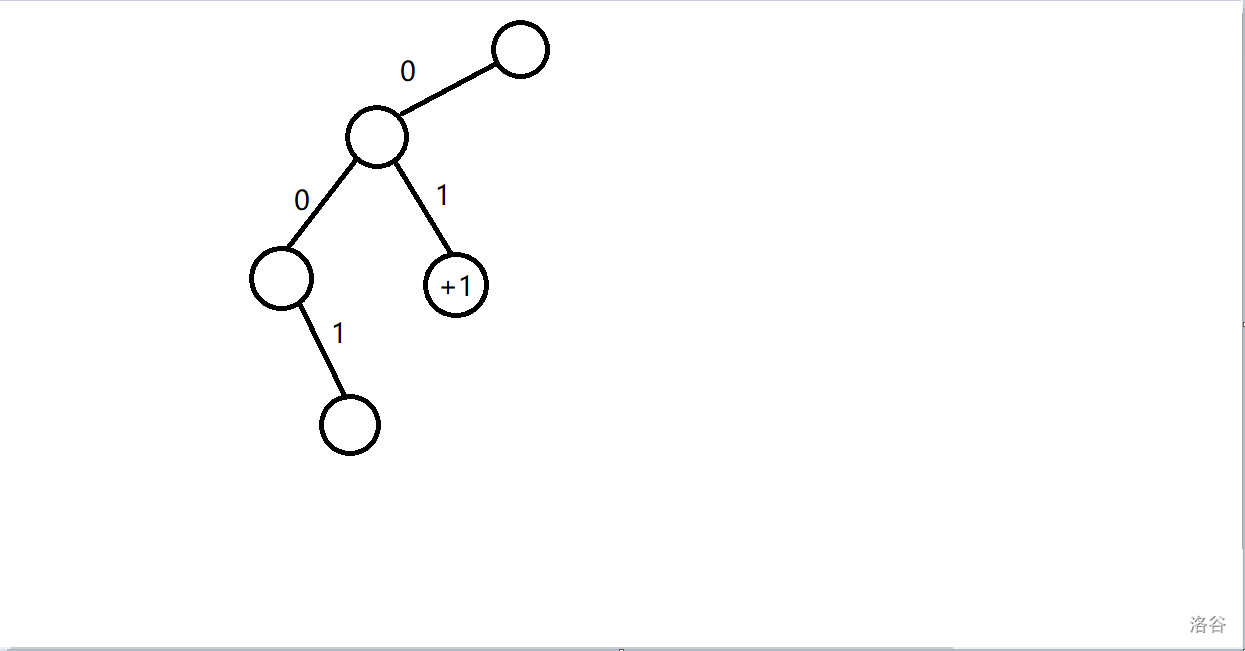
-
对于最后一位,我们发现 这位等于 或 都能产生贡献,所以都打一个 的标记。
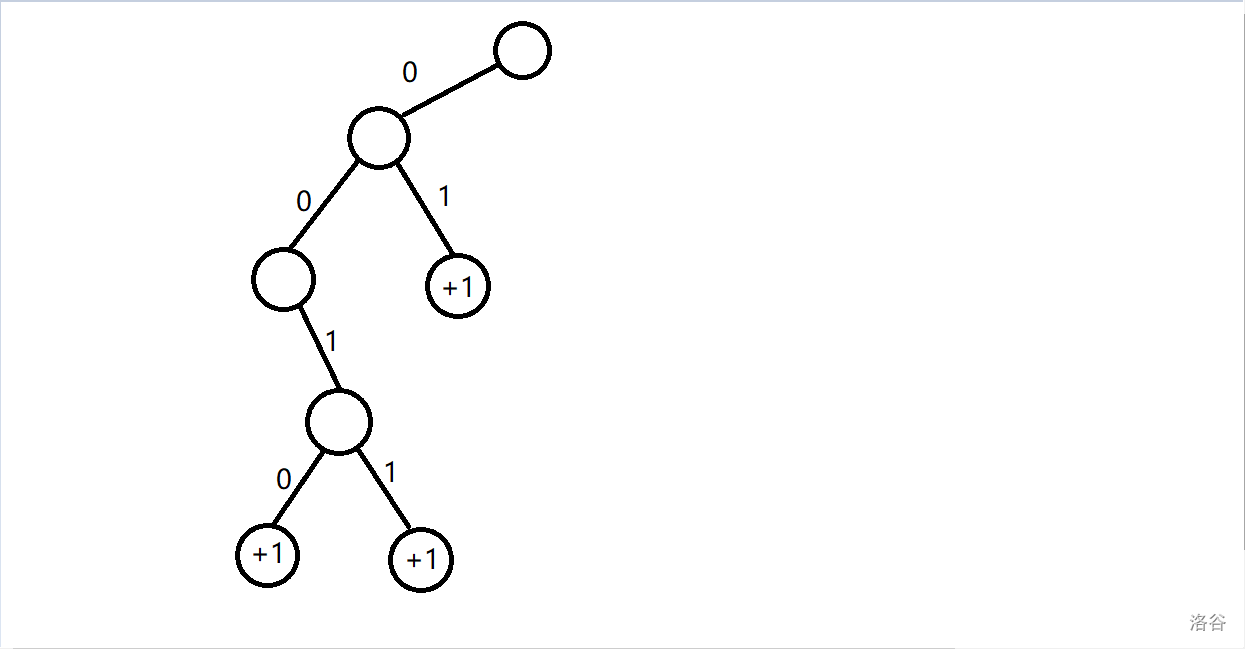
当 时,。
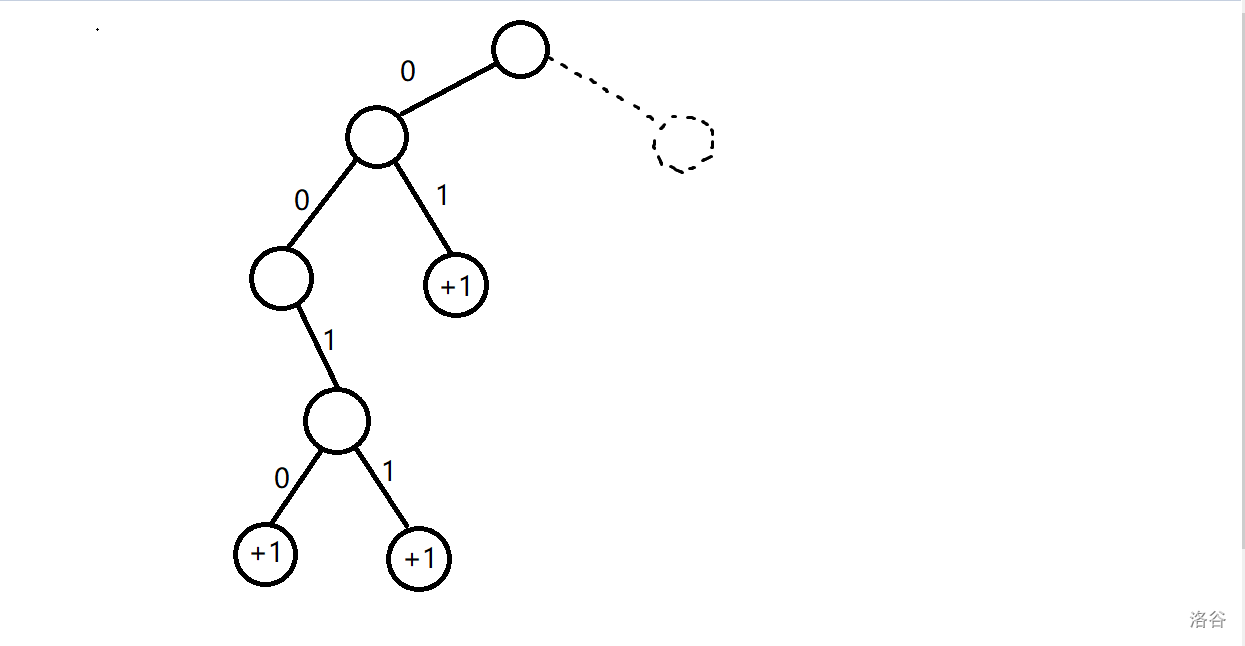
当 时,。
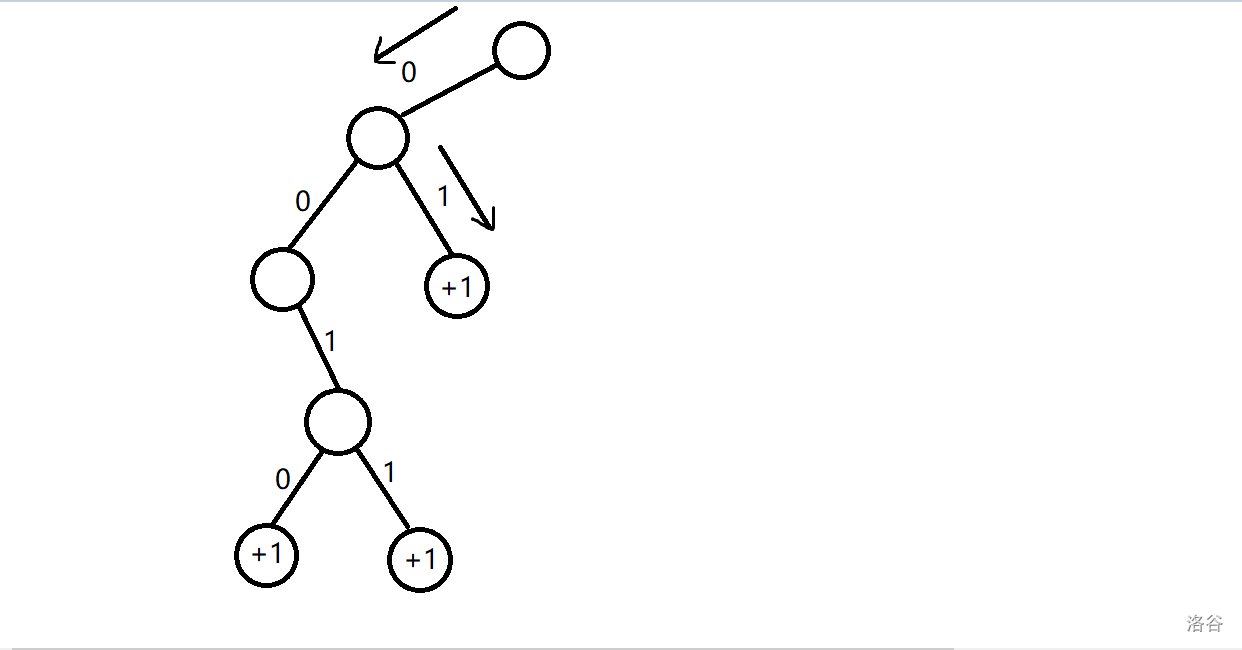
当 时,。
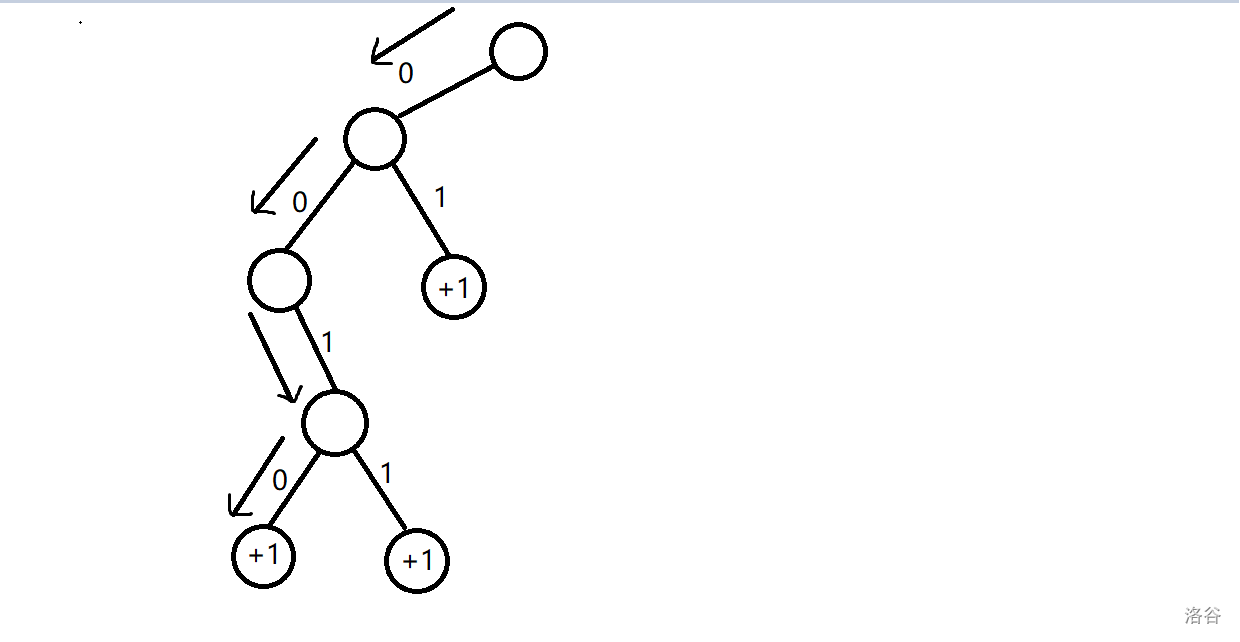
复杂度:
建立节点时我们最多只会往一边去建立节点,所以是 的,而查询时也是只会走 层的,所以时间复杂度 。
code:
#include<bits/stdc++.h> using namespace std; int tot; int a[500010],b[500010]; struct Tree{ int ch[2],val; Tree(){ memset(ch,0,sizeof(ch)); } }tr[16000010]; int f=0; void insert(int x,int y){ int p=0; for(int i=31;i>=0;i--){ int k1=(x>>i)&1,k2=(y>>i)&1,q; if(i==0){ if(k2==0){ q=k1; if(tr[p].ch[q]==0) tr[p].ch[q]=++tot; tr[tr[p].ch[q]].val++; }else{ q=k1; if(tr[p].ch[q]==0) tr[p].ch[q]=++tot; tr[tr[p].ch[q]].val++; q=k1^1; if(tr[p].ch[q]==0) tr[p].ch[q]=++tot; tr[tr[p].ch[q]].val++; } continue; } if(k2==1){ q=k1; if(tr[p].ch[q]==0) tr[p].ch[q]=++tot; tr[tr[p].ch[q]].val++; q=k1^1; if(tr[p].ch[q]==0) tr[p].ch[q]=++tot; p=tr[p].ch[q]; }else{ q=k1; if(tr[p].ch[q]==0) tr[p].ch[q]=++tot; p=tr[p].ch[q]; } } } int query(int x){ int p=0,ans=0; for(int i=31;i>=0;i--){ int q=(x>>i)&1; if(tr[p].ch[q])ans+=tr[tr[p].ch[q]].val,p=tr[p].ch[q]; else break; } return ans; } signed main(){ ios::sync_with_stdio(false); cin.tie(0);cout.tie(0); int T,n,q; cin>>T>>n>>q; for(int i=1;i<=n;i++)cin>>a[i]; for(int i=1;i<=n;i++)cin>>b[i],insert(a[i],b[i]); int lst=0; while(q--){ int k; cin>>k; k=k^(lst*T); lst=query(k); cout<<lst<<'\n'; } return 0; }
- 1
信息
- ID
- 10899
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
