自动搬运

查看原文

来自洛谷，原作者为

	normalpcer 代词使用他/她/它 || 被 define int long long 吓晕

搬运于2025-08-24 23:05:15，当前版本为作者最后更新于2024-10-21 17:44:18，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意简述

给定一棵树，希望给其上的所有点编号，使得所有边的两端端点编号之和均不超过 $N+1$。

分析

可以使用如下的贪心策略进行编号：

• 按照从深到浅的顺序排序所有点。
• 按照顺序，将一个点编上尽可能大的号码，同时，如果它的父节点没有被编号，则将其父节点编上尽可能小的号码。

接下来，我们对这个策略的正确性进行一个简要的证明。

使用数学归纳法。我们称在一个拥有 $N$ 个节点的子树上，使用 $\left[L, R\right]$ 区间中的整数进行编号为一次操作 $\operatorname{F}\left(N, L, R\right)$。这个操作的结果合法，当且仅当所有边两端端点的编号之和不超过 $L+R$。为了方便，我们称这个编号之和为这个边的“值”，并记点 $V$ 的编号为 $id_V$。接下来我们证明这个操作的结果合法。

对于 $N=1$ 和 $N=2$ 的情况，这种操作的结果必然合法。

假设 $N=k$ 和 $N=k-1$ 时，$\operatorname{F}\left(k, L, R\right)$ 的结果合法，不妨再令 $N=k+1$。在此时进行操作 $\operatorname{F}\left(k+1, L, R\right)$

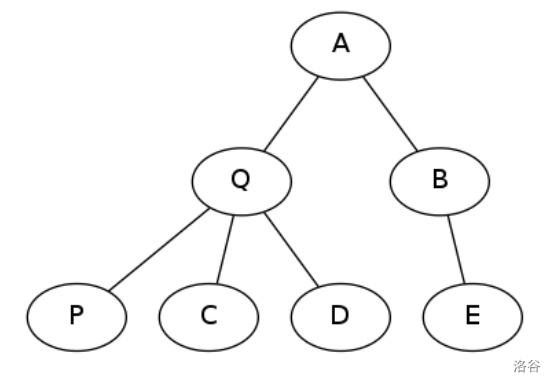
我们设要编号为 $R$ 的点为 $P$，它的父节点为 $Q$。不妨考虑将 $P, Q$ 两点去掉，此时原图会分裂成若干个子树（对于上图，三个子树为 $C$, $D$ 和 $ABE$）。将这三个子树以任意方式连接，则是一个包含 $k-1$ 节点的树。

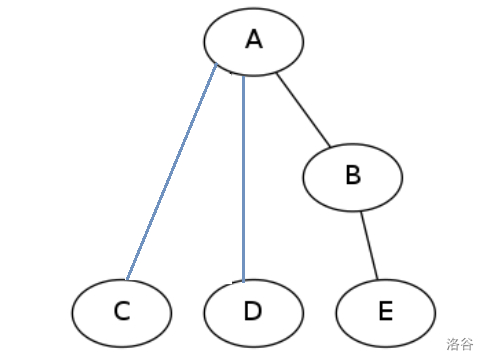
如图，我们把 $P, Q$ 去掉，并分别编上号码 $R$ 和 $L$，然后添上两条新的边（$AC, AD$），这样就是一棵树。对这棵树执行操作 $\operatorname{F}\left(k-1, L+1, R-1\right)$ 即可。那么，剩余的几条边和蓝边都能够保证它们的值不超过 $L+R$。

接下来，考虑这个过程中去掉的边（$QP, QC, QD$），对于 $QP$，它的值为 $L+R$，是合法的。对于 $Q$ 和它的一个子节点 $S$ 的连线，必然有 $L+1 \le id_S \le R-1$，这个边的值 $v = L + id_S \le L+R-1$，也是合法的。故此次操作的结果是合法的。

特别地，考虑 $Q$ 已经有编码的情况。事实上，这种情况更加简单，对于去掉点 $P$ 的子树，我们可以执行操作 $\operatorname{F}\left(k, L, R-1\right)$，那么所有边的值都能保证 $v \le L+R-1$，而新连的边值为 $L+R$，依旧合法。

故由数学归纳法，原命题成立。操作 $\operatorname{F}\left(N, 1, N\right)$ 的结果即为本题答案。

代码

这里不多加阐述，可以参考下方的代码和注释。

/**
 * @link https://www.luogu.com.cn/problem/P11206
 */

#include <bits/stdc++.h>
#define upto(i,n) for(int i=1;i<=(n);i++)

int T;
namespace Solution {
    int N;
    const int _N = 1e5+5;

    int depth[_N];  // 到根节点（1）的距离

    std::vector<int> conn[_N];  // i 和 conn[i][j] 互相连接
    int parent[_N];  // 记录父亲节点
    int filling_queue_arr[_N];
    int filled[_N];
    std::queue<int> filling_queue;
    
    void init() {
        // 重设，防止多测数据互相污染
        std::memset(depth, 0, sizeof(depth));
        upto(i, _N)  conn[i].clear();
        std::memset(parent, 0, sizeof(parent));
        std::memset(filling_queue_arr, 0, sizeof(filling_queue_arr));
        std::memset(filled, 0, sizeof(filled));
        scanf("%d", &N);
        int x=0, y=0;
        upto(_, N-1) {
            scanf("%d%d", &x, &y);
            conn[x].push_back(y);
            conn[y].push_back(x);
        }
    }

    void dfs_depth(int p, int prev) {  // 计算深度
        parent[p] = prev;
        depth[p] = depth[prev] + 1;

        for (auto &dest: conn[p]) {
            if (dest == prev)  continue;
            dfs_depth(dest, p);
        }
    }

    bool check() {
        upto(i, N) {
            for (auto &dest: conn[i]) {
                if (filled[i] + filled[dest] > N+1) {
                    return false;
                }
            }
        }
        return true;
    }

    void solve() {
        init();
        dfs_depth(1, 0);  // 以 1 为根节点
        // 按照深度排序填充顺序
        upto(i, N)  filling_queue_arr[i] = i;
        std::sort(filling_queue_arr+1, filling_queue_arr+1+N, [](auto a, auto b) {
            return depth[a] > depth[b];
        });
        upto(i, N)  filling_queue.push(filling_queue_arr[i]);  // 压入队列

        int L=1, R=N;  // 区间最小值和最大值
        // 依次填充
        while (not filling_queue.empty()) {
            auto cur = filling_queue.front();  filling_queue.pop();
            if (filled[cur])  continue;  // 填过的就忽略
            // 尝试在该点填充一个最大的数
            filled[cur] = R; R--;
            // 在父节点填充一个最小的数
            if (parent[cur] != 0 /* 特判，根节点不做处理 */ && not filled[ parent[cur] ]) {
                filled[ parent[cur] ] = L; L++;
            }
        }

        // 全部填充完毕
        upto(i, N)  printf("%d ", filled[i]);
        assert(check());  // 结果正确
        printf("\n");
    }
}


int main() {
    scanf("%d", &T);
    while (T --> 0)
        Solution::solve();
    return 0;
}

这里的 check() 函数事实上是无用的，不过可以方便调试。

此外，还是要提醒一下，对于多测的题目，要注意完全清空所有可能用到的数组和容器。