自动搬运

查看原文

来自洛谷，原作者为

	Twlight！ 追求真理之人不可心存傲慢，不可嘲笑无法用科学解释的奇迹，不可回避这个世界的美丽。

搬运于2025-08-24 23:05:08，当前版本为作者最后更新于2024-10-23 16:26:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

逛题目列表时发现的题目，分享后被 @H3PO4 秒了，特此膜拜（%%%）。

题目大意

平面上有一个 $N$ 个点的简单多边形（点按顺序给出，令其为 $P_i$），和一个点 $O$，每次可以询问图中任意三个点是否是逆时针排列，判断点 $O$ 是否在这个多边形内部。保证点两两不同、无三点共线、且多边形线段不相交。

三个点 $A, B, C$ 逆时针排列的定义为：站在点 $A$ 看向点 $B$ 时，点 $C$ 在直线 $AB$ 的左侧，如题图，左侧 $A，B，C$ 成逆时针排列。

前置知识：射线法

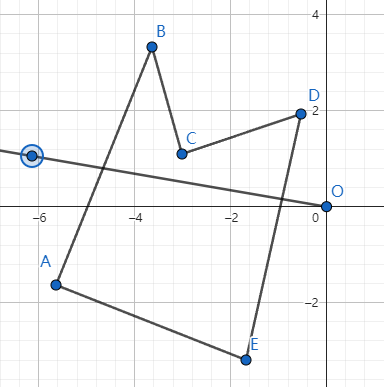
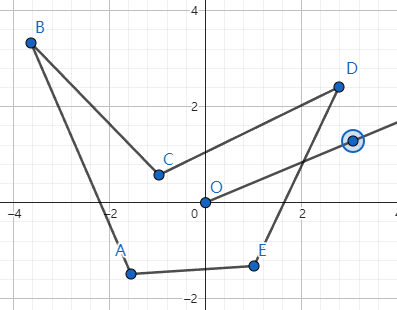
简单地说，判断一点是否在多边形内，可以从该点向任意方向引出一条射线，若射线与多边形有奇数个交点，那么该点在多边形内，否则在多边形外，如图：

图1中点 $O$ 引出的射线与多边形有 $2$ 个交点，而图2中有 $1$ 个交点，故图1中 $O$ 点在多边形外部，图二中 $O$ 则在多边形内部。

简易证明：

首先得知道，一个多边形只会把平面分成两部分，一部分是在多边形内的，另一部分是在多边形外的，因此一个点只有在内、在外两种状态（这里不讨论在多边形上的情况）。

从一点出发沿着射线方向走，每穿过一次多边形，都会改变自己的状态（也就是从内部到外部，或从外部到内部），而沿着射线方向走总会走到多边形外部，因此只需要知道穿过次数的奇偶性，就可以逆推回去。

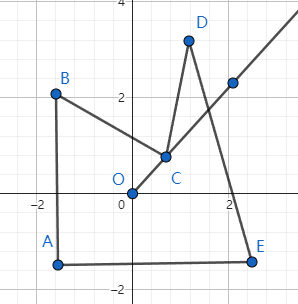
但是这样说是有缺陷的，如图：

当点 $C$ 在射线上时，它不应该算作穿过了一次多边形，因为经过它没有改变点的状态。因此，有些时候我们并不能仅判断交点数量，而是要判断改变状态的次数（也就是穿过多边形的次数）。

如此地，我们就可以证明上述方法的正确性。

回到本题

知道了上述结论，我们就需要从点 $O$ 引出一条射线，判断交点的数量。因为不能加点，不妨以点 $P_1$ 为方向，先引出射线 $OP_1$。

那么就来到了第二个问题，如何判断一条线段是否与射线相交呢？

图中的点是顺序给出的，因此我们可以知道如果一条线段与射线相交，它们两端的端点一定在异侧（因为题目无三点共线）。这样我们就可以询问 $N - 1$ 次，判断每个点与直线 $OP_1$ 的关系（在上边/下边），如图：

然后就可以得出每个线段与直线 $OP_1$ 是否相交。

但是这样会产生两个问题，首先便是我们判断的是线段与直线的关系，而我们用的是射线法。其次，这样也并不能直接根据相交线段的数量而判断，而是要看判断改变状态的次数，这在上方证明时就已提过。

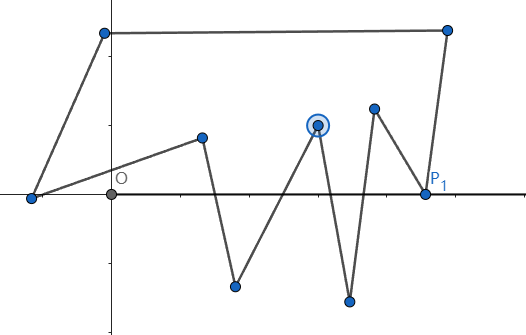
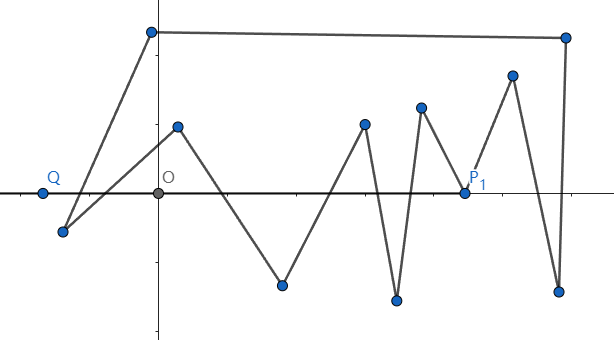
但是，第二个问题是好解决的，如果射线途中不经过多边形的任何端点，那么答案就等于与射线相交的线段数量。而题目保证了无三点共线，因此我们考虑换一下，以 $O$ 为起点，$P_1O$ 方向为射线方向，如图：

为了方便，设此时射线为 $OQ$，则 $OQ$ 只会与某些线段相交，而不会经过顶点。

我们钦定 $P_1O$ 方向为左方向，此时点 $O$ 一定在直线 $P_1P_2$ 或者 $P_1P_n$ 的左边（询问要按从下往上的顺序，类似坐标系一样，这样才能保证统一性），不妨选直线 $P_1P_2$ 作为判断基准。

因为你不知道这个左方向到底是什么，所以你需要询问直线 $P_1P_2$ 与 $O$ 的关系，钦定这个返回值为左。往后统计答案时，判断询问 $P_iP_{i+1}$ 与 $O$ 的返回值是否与先前规定的左方向的返回值相同即可，这样共询问 $N - 1$ 次，总询问次数为 $2N - 2$ 次，符合题目条件。

至此我们就解决了这个问题的 $90\%$，剩余的便是小细节：前文提到，查询时是有方向的，确定一个点与直线的方向时要统一询问时的直线方向，具体细节可见代码。

参考代码

#include <bits/stdc++.h>
#define ll long long
const int N = 500 + 10;
using namespace std;

int read () {
	int x = 0, k = 1; char c = getchar();
	while (c < '0' || c > '9') { if (c == '-') k = -1; c = getchar(); }
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
	return (1ll * x * k);
}

int n, q;
int dire[N], lft, cnt;

int query (int A1, int A2, int p) { 
	return printf("? %d %d %d\n", A1, A2, p), cout.flush(), read(); 
}

signed main() {
	n = read(), q = read();

	// 询问每个点与直线 OP1 的关系（上下） 
	for (int i = 2; i <= n; ++i) dire[i] = query(0, 1, i);

	// 钦定 P1P2 与 O 询问的返回值为左方向，注意要从下往上 
	lft = dire[2] ? query(1, 2, 0) : query(2, 1, 0);

	for (int i = 3; i <= n; ++i)
		if (dire[i] != dire[i - 1]) // 判断是否与直线相交 
			if ((dire[i] ? query(i, i - 1, 0) : query(i - 1, i, 0)) == lft) // 判断是否与射线相交 
				++cnt;

	printf("! %d\n", cnt & 1);

	return 0;
}

时间复杂度：$O(N)$。

参考文献

1. 判断一点是否在任意多边形内部
2. 判断点是否在多边形内（射线法）
3. @H3PO4 的神秘口糊（%%%）