自动搬运

查看原文

来自洛谷，原作者为

	hhiron 忽悟格物致知之旨，圣人之道，吾性自足，不假外求。

搬运于2025-08-24 23:04:54，当前版本为作者最后更新于2024-10-05 18:52:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

路径分析

首先题目规定路径可以经过重复点和重复边。我们考虑能否优化这种叙述。走过的边无非就两种情况：

1、该边被经过了奇数次，根据异或的性质，这种情况等价于该边只走了一次。

2、该边被经过了偶数次。对于一幅图，我们删去其中经过偶数次的边，然后由于每个偶数边的进入离开次数都为偶数，我们可以把这些进入和出去的边两两相连，直到图中没有偶数边为止，这样一直操作过后走过的路径依然合法。根据异或的性质，偶数边的代价记为 $0$，则删后的代价与原代价相等，视为等价。

以下图为例，其中黑色的箭头代表原来经过的情况，那么红色的 $e$ 边被经过了两次，如果我们删掉红色的 $e$ 边，将四条黑边改成如图所示的绿边，则原路径依然联通，只需要改变几个边的方向即可视为等价。

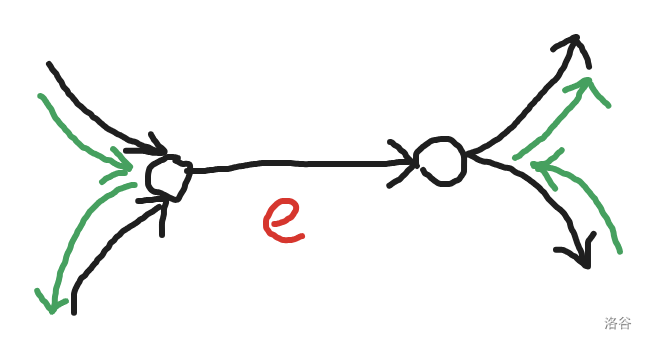
特殊图分析

根据以上两条性质，我们仅需要考虑简单路径即可 (指每条边仅被经过一次)。

有了以上的性质，我们考虑这张图为树的情况，那么一个合法的构造方案显然可以将各个边的长度 $w(u_i,v_i)$ 赋值为 $f(u_i,v_i)$。

题目中的图与树不同的本质在于有环，因此我们考虑简单环，记一个环上各个边的 $f(u_i,v_i)$ 的异或和为 $a$。模拟一下样例可以发现当 $a$ 的值为 $0$ 时合法。因为对于任意两个相邻的节点 $u,v$， 将它们之间边的长度 $w(u,v)$ 赋值为 $f(u,v)$，则无论从环的哪个方向走，路径的权值一定为 $w(u,v)$ 或 $w(u,b) \oplus a$。不难发现这种构造一定满足。

接下来考虑必要性，假设 $a$ 不为 $0$，那么必然存在一个最高位异或后的结果为 $1$，设这一位为第 $k$ 位，也必然存在两个相邻的节点 $u,v$，它们的 $f(u,v)$ 的第 $k$ 位也为 $1$，根据异或的性质，由于 $a$ 的第 $k$ 位为 $1$ 那么 $a\oplus f(u,v)<f(u,v)$。这反映在路径上是指不直接到达，反方向绕一圈的情况，该情况的代价比 $f(u,v)$ 小，与题目中 $f(u,v)$ 为最小路径代价矛盾。因此我们得出：当且仅当对于图中所有的环，环上每一条边的 $f(u,v)$ 的异或和为 $0$ 时有解，且构造的方式为将各个边的长度 $w(u,v)$ 赋值为 $f(u,v)$。

结论

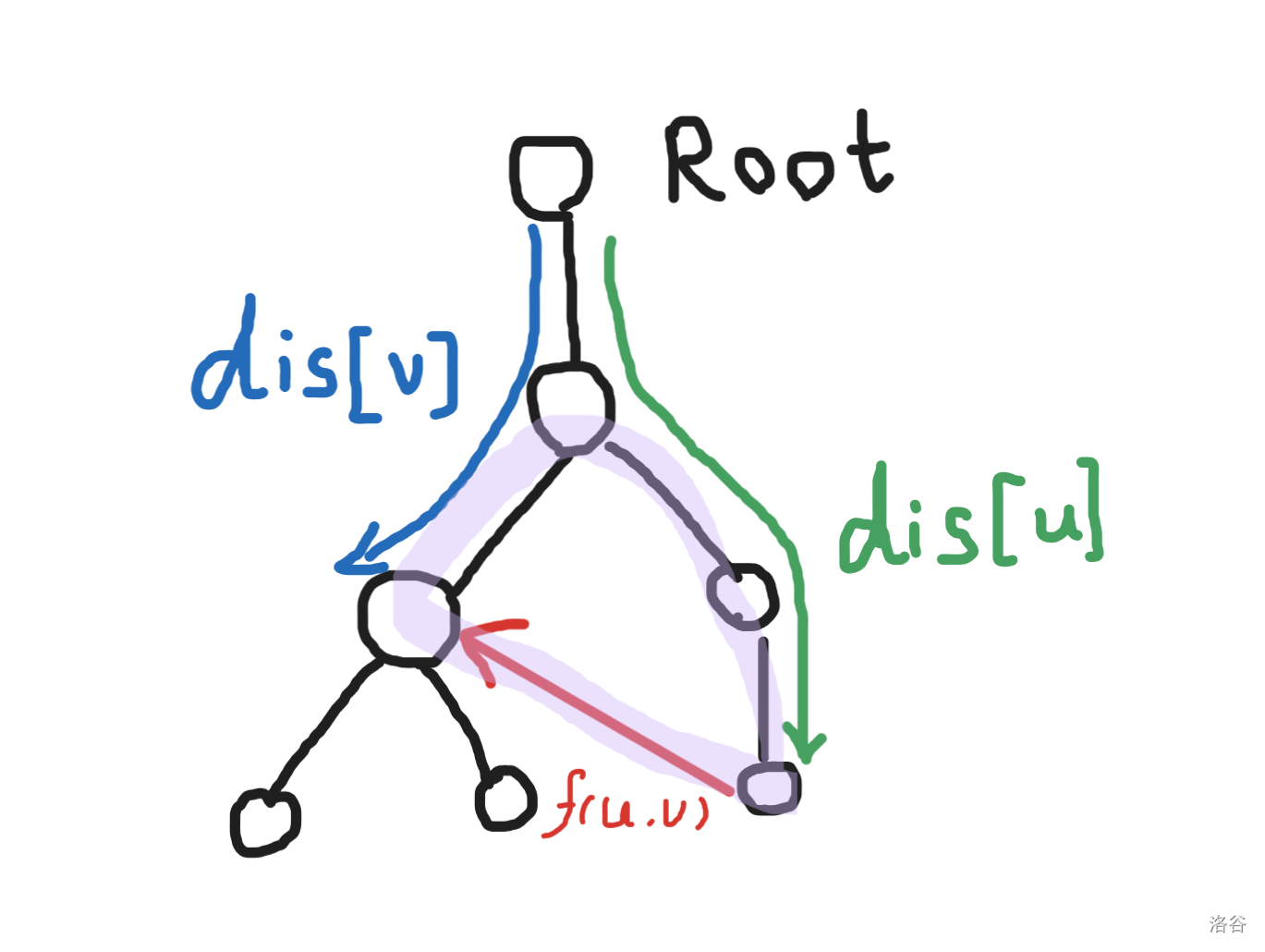
最后将环和树结合起来考虑，可以将题目中给定的图视作一棵树和若干环构成，我们可以在遍历树上节点的时候找到环，运用类似树上差分的操作，计算出每个环的异或长度，判断该异或值是否为 $0$ 即可。具体的，在DFS时记录每个节点到根节点的异或和 $dis[u]$，$dis[u]=dis[fa]\oplus f(fa,u)$，当发现某条边 $e(u,v)$ 指向已经被遍历过的点时可以算出这个环的异或和 $dis[u]\oplus dis[v]\oplus f(u,v)$，最后判断它是否为 $0$ 即可。

结合下图理解，其中蓝色代表 $dis[v]$ ，绿色代表 $dis[u]$ ，红色代表一条指向已被遍历过的点的边，构成一个紫色的环。不难发现紫色环的各边异或和等于红，绿，蓝三个值的异或和。

code

最丑的环节：

#include<bits/stdc++.h>
#define INF 0x7fffffff
typedef long long ll;
using namespace std;
const int N=1e6+6;
int n,m,tot=0,head[N],a[N];
struct node{
	int nxt,to,w;
}e[N<<2];
void addEdge(int u,int v,int w){
	e[++tot]=(node){head[u],v,w};
	head[u]=tot;
	e[++tot]=(node){head[v],u,w};
	head[v]=tot;
}
int dis[N];
bool ans=1;
void dfs(int u){
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(dis[v]!=-1){
			if(dis[u]^e[i].w^dis[v]) ans=0;
			continue;
		}
		dis[v]=dis[u]^e[i].w;
		dfs(v);
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,x,y,z;i<=m;i++){
		scanf("%d%d%d",&x,&y,&z);
		addEdge(x,y,z); a[i]=z;
	}
	for(int i=1;i<=n;i++) dis[i]=-1;
	for(int i=1;i<=n;i++){
		if(dis[i]==-1){
			dis[i]=0;
			dfs(i);
		} 
	}
	if(ans){
		puts("Yes");
		for(int i=1;i<=m;i++) printf("%d ",a[i]);
	}else puts("No");
	return 0;
}

这是蒟蒻的第一篇题解，如有不足，欢迎指正。