自动搬运

查看原文

来自洛谷，原作者为

	godmoo 凌空蹈虚，难成千秋之业 / 求真务实，方能善作善成

搬运于2025-08-24 23:04:12，当前版本为作者最后更新于2025-08-19 15:46:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

Link & Cnblogs.

图论好题，但我比赛时就没有往边双上想啊啊啊。。。

题意： 给定一个 $n$ 个点 $m$ 条边的带权无向图，可能有重边，无自环。对于每个节点 $u \neq 1$，求出一条迹 $1 \rightsquigarrow u$，最小化迹上的边权最大值与边权最小值的和。$n, m \le 3 \times 10 ^ 5, w \le 10 ^ 9$。

$\mathbf{Subtask~3.~}$ 所有一端点是 $\mathbf 1$ 的边的边权为 $\mathbf{10 ^ 9}$

那么所有迹上的边权最大值均为 $10 ^ 9$，我们仅需求出边权最小值最小的迹。迹相关问题，不妨从边连通性的角度考虑。

我们知道，$1 \rightsquigarrow u$ 上的桥是必选的，考虑进行边双缩点，那一个边双内贡献怎么处理呢？实际上，我们有如下引理：

$\mathbf{Lemma~1.}$ 边双中，对于任意一点 $x$ 和任意一边 $e$，存在经过 $x, e$ 的回路。

$\mathbf{Lemma~2.}$ 边双中，对于任意两点 $x, y$ 和任意一边 $e$，存在 $x \rightsquigarrow e \rightsquigarrow y$ 的迹。

上述引理中的斜体名词的解释参考 OI-Wiki / 图论相关概念 / 路径。

$\mathbf{Proof.}$

由 Menger 定理，我们有如下基本事实：边双中，对于任意两点 $x, y$，存在经过 $x, y$ 的回路。

对于 $\mathbf{Lemma~1.}$：

• 令 $e = (u, v)$，新建虚点 $w$ 并将 $e$ 视作 $(u, w)$ 和 $(w, v)$，则删去 $(u, w)$ 或 $(w, v)$ 都等价于原图删去 $e$，不改变边连通性。
• 由基本事实，存在经过 $x, w$ 的回路，这条回路必然经过 $u, v$，于是该回路是符合条件的回路。$\square.$

对于 $\mathbf{Lemma~2.}$：

• 由 $\mathbf{Lemma~1.}$，存在经过 $x, e$ 的回路 $C_x$，当存在 $C_x$ 使得 $y \in C_x$ 时满足条件

• 同理，存在经过 $y, e$ 的回路 $C_y$，当存在 $C_y$ 使得 $x \in C_y$ 时满足条件。

• 排除上述特殊情况，$C_x, C_y$ 有公共边 $e$，$x, y$ 均不在 $C_x, C_y$ 的公共边（集）上，那么直接从 $x$ 通过 $C_x$ 走到 $e$，再按照走过 $e$ 的方向（顺/逆时针）通过 $C_y$ 走到 $y$ 即可。$\square.$

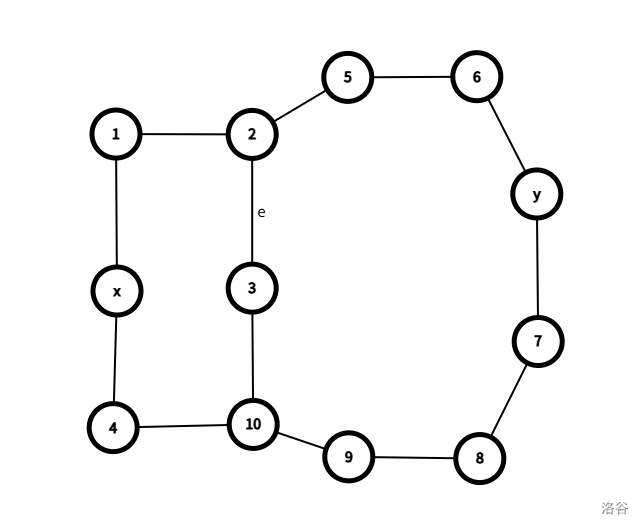
$\mathbf{Lemma~2.}$ 说明，对于一个边双，我们总可找到一条路径经过其内部边权最小的边。于是我们建出边双缩点树，将每个边双对应点的点权设为其内部最小边权，以节点 $1$ 的对应点为根做一遍 dfs 即可求出答案。$\mathcal O(n + m)$。

$\mathbf{Subtask~7.~n, m \le 2000}$

往 $\mathbf{Subtask~3.}$ 去靠：将所有边按边权从小到大排序，依次加边。加到边 $(u, v, w)$ 时，钦定边权最大值为 $w$，套用 $\mathbf{Subtask~3.}$ 的做法再加上 $w$ 更新答案。$\mathcal O(n ^ 2 + nm)$。

$\mathbf{Subtask~8.~n \le 5000}$

$m$ 没有特殊性质了，但注意到很多边是没用的：考虑新增边 $(u, v, w)$，由于 $\mathbf{Subtask~3.}$ 的做法仅依赖连通性和边双连通性，于是若 $u, v$ 已双连通，因为我们是按 $w$ 升序加边的，这条边一定是没有贡献的。

考虑维护，用两个并查集分别维护连通性和边双连通性即可。显然有用边仅有 $2(n - 2)$ 条。

套用 $\mathbf{Subtask~7.}$ 做法可做到 $\mathcal O(n ^ 2 + m\log m)$。

::::success[Code: Connectivity]

namespace Connectivity {
    struct DSU {
        int fa[N];
        void init(){ iota(fa + 1, fa + n + 1, 1); }
        int find(int u){ return u == fa[u] ? u : fa[u] = find(fa[u]); }
        void merge(int u, int v){ fa[u] = v; }
    } C, EDC;
 
    void init(){ C.init(), EDC.init(); }
    int merge(int u, int v){
        int uf, vf;
        if((uf = C.find(u)) != (vf = C.find(v))) return C.merge(uf, vf), 0;
        else if((uf = EDC.find(u)) != (vf = EDC.find(v))) return EDC.merge(uf, vf), 1;
        else return 2;
    }
} using namespace Connectivity;

::::

$\mathbf{Subtask~10.~}$ 正解

考虑对加边过程动态维护最小边权。我们将有用边分为两类：

• 影响连通性的边： 这即为 Kruskal 求 MST 的过程，这样的边一定在 MST 上，于是我们提前建出 MST（以 $1$ 为根），在 MST。 对于每个连通块，它一定是最小生成树的一个连通子图，钦定深度最小的点为该连通块的根。这样，每个连通块都是 MST 的一个子树（可能残缺）。

• 影响边双连通性的边： 考虑该边两端点 $u, v$ 当前所属的连通块的边双缩点树，$(u, v)$ 与树上 $u \rightsquigarrow v$ 构成一个环，缩起来即可。 拉到 MST 上考虑，该连通块是 MST 的一个子树，在 MST 上加边和缩点。

考虑维护节点 $i$ 到节点 $1$ 最小边权 $f_i$。

对于影响连通性的边 $(u, v, w)$，钦定 $v$ 是 $u$ 在 MST 上的父亲，转移式：

$$f_x \gets \min(f_x, w), x \in \operatorname{subtree}(u) $$

对于影响边双连通性的边 $(u, v, w)$，将 MST 上 $u \rightsquigarrow v$ 上所有点缩起来，转移式

$$f_x \gets \min(f_x, w, f_u, f_v), x \in \operatorname{subtree}(\operatorname{lca}(u, v)) $$

每个连通块都是 MST 的一个子树（可能残缺），以上两种转移均可以在 MST 上用 dfs 序 + 线段树维护即可。再开一棵线段树，在加入影响边双连通性的边时，用 $\min(w, f_u, f_v) + w$ 去更新子树的答案。

::::info[为什么在加入影响连通性的边时不用更新答案的线段树？] 因为在与 $1$ 合并前更新没有意义，与 $1$ 合并后不会再作为儿子被更新 ::::

还没完。拉到 MST 上维护确实让问题更简单了，但这会影响到每个连通块的独立性。具体的，原来可能没连通的一部分，也在某次子树修改中被改到，虽然这样的 $f$ 是对的，但是这个东西算早了，导致可能还没有合并这个子树和节点 $1$ 就已经用不合法的 $w$ 更新了答案。

解决方式也很简单，一个连通块与节点 $1$ 所在连通块合并时，用当前的 $w$ 重算一遍该连通块的答案即可。

$\mathcal O(n \log n + m \log m)$。没了，将近 4k，应该是我的问题。

::::success[Code]

// godmoo's code
#include <bits/stdc++.h>
#define eb emplace_back
#define ep emplace
#define fi first
#define se second
#define mkp make_pair
#define lbd lower_bound
#define ubd upper_bound
#define mathmod(a) (((a) % MOD + MOD) % MOD)
#define mem(a, b) memset(a, b, sizeof(a))
#define cpy(a, b) memcpy(a, b, sizeof(b))
#define ckmx(a, b) (a = max(a, b))
#define ckmn(a, b) (a = min(a, b))
#define all(a) a.begin(), a.end()
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef tuple<int, int, ll> t3;
const int N = 3e5 + 5;
const ll INF = 0x3f3f3f3f3f3f3f3fll;
int n, m, in[N], out[N], tim, ft[N], dep[N];
vector<int> G[N];
vector<t3> E;
namespace Connectivity {
    struct DSU {
        int fa[N];
        void init(){ iota(fa + 1, fa + n + 1, 1); }
        int find(int u){ return u == fa[u] ? u : fa[u] = find(fa[u]); }
        void merge(int u, int v){ fa[u] = v; }
    } C, EDC;
 
    void init(){ C.init(), EDC.init(); }
    int merge(int u, int v){ return ((u = C.find(u)) != (v = C.find(v))) ? (C.merge(u, v), 0) : 1; }
    int check(int u, int v){
        int uf, vf;
        if((uf = C.find(u)) != (vf = C.find(v))) return 0;
        else if((uf = EDC.find(u)) != (vf = EDC.find(v))) return 1;
        else return 2;
    }
} using namespace Connectivity;
 
struct SegTree{
    ll f[N << 2];
    void pushdown(int u){ ckmn(f[u << 1], f[u]), ckmn(f[u << 1 | 1], f[u]), f[u] = INF; }
    void build(){ mem(f, 0x3f); }
    void modify(int u, int l, int r, int ql, int qr, ll x){
        if(ql <= l && r <= qr) return ckmn(f[u], x), void();
        int mid = l + r >> 1; pushdown(u);
        if(ql <= mid) modify(u << 1, l, mid, ql, qr, x);
        if(qr > mid) modify(u << 1 | 1, mid + 1, r, ql, qr, x);
    }
    void change(int u, int l, int r, int p, ll x){
        if(l == r) return f[u] = x, void();
        int mid = l + r >> 1; pushdown(u);
        p <= mid ? change(u << 1, l, mid, p, x) : change(u << 1 | 1, mid + 1, r, p, x);
    }
    ll query(int u, int l, int r, int p){
        if(l == r) return f[u];
        int mid = l + r >> 1; pushdown(u);
        return min(f[u], p <= mid ? query(u << 1, l, mid, p) : query(u << 1 | 1, mid + 1, r, p));
    }
} T1, T2;
 
int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    for(int i = 1, u, v, w; i <= m; i++) cin >> u >> v >> w, E.eb(u, v, w);
    sort(all(E), [](t3 x, t3 y){ return get<2>(x) < get<2>(y); }), init();
    for(auto [u, v, w] : E) if(!merge(u, v)) G[u].eb(v), G[v].eb(u); // MST
 
    function<void(int, int)> dfs = [&](int u, int fa){
        in[u] = ++tim, ft[u] = fa, dep[u] = dep[fa] + 1;
        for(int v : G[u]) if(v != fa) dfs(v, u);
        out[u] = tim;
    }; dfs(1, 0);
 
    T1.build(), T2.build(), init();
 
    for(auto [u, v, w] : E){
        int res = check(u, v);
        if(!res){
            if(dep[u] < dep[v]) swap(u, v);
            T1.modify(1, 1, n, in[u], out[u], w), C.merge(u, v);
            function<void(int, int, ll)> upd = [&](int u, int fa, ll w){
                if(C.find(u) != 1) return;
                T2.change(1, 1, n, in[u], T1.query(1, 1, n, in[u]) + w);
                for(int v : G[u]) if(v != fa) upd(v, u, w);
            }; upd(u, v, w);
        }
        else if(res == 1){
            u = EDC.find(u), v = EDC.find(v);
            ll wgt = min({w, T1.query(1, 1, n, in[u]), T1.query(1, 1, n, in[v])});
            while(u != v){
                if(dep[u] < dep[v]) swap(u, v);
                EDC.merge(u, ft[u]), u = EDC.find(u);
            }
            T1.modify(1, 1, n, in[u], out[u], wgt);
            T2.modify(1, 1, n, in[u], out[u], wgt + w);
        }
    }
     
    for(int i = 2; i <= n; i++) cout << T2.query(1, 1, n, in[i]) << "\n";
    cout << flush;
    return 0;
}

::::