自动搬运

查看原文

来自洛谷，原作者为

	chenly8128 God helps those who help themselves.

搬运于2025-08-24 23:03:26，当前版本为作者最后更新于2024-08-26 19:53:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

难是不难，但是细节挺多的。

思路：列表+找规律

实现：部分打表+预处理+分段查询

思路部分

列表

我们从 $i = 3$ 开始，对于 $f(i)$ 列表（$i = 1$ 或者 $n = 2$ 可以特判，答案都是 0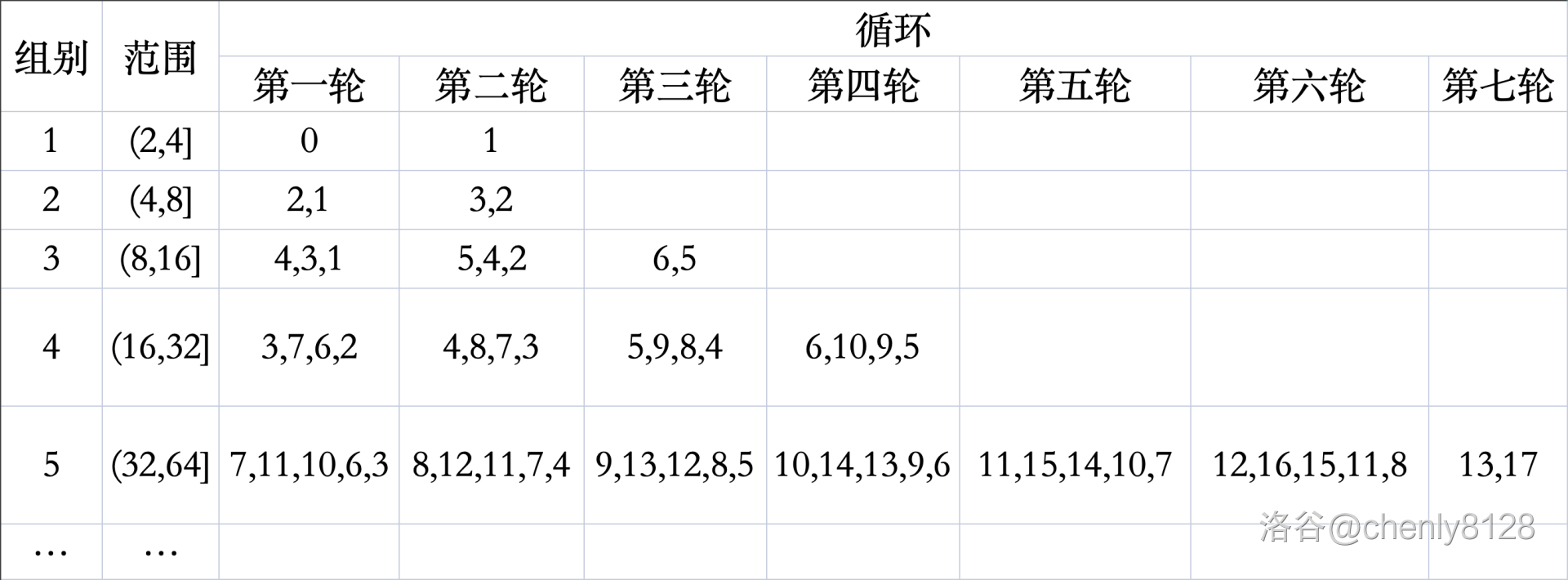）。 表格中列出了 $i$ 与 $f(i)$ 的关系。可以清晰的看到，对与第 $k$ 组，$i \in \left ( 2^k,2^{k+1}\right ]$。而在这个范围内的 $i$ 按照 $k$ 个数为一轮的规律循环（最后一轮特例），每一轮每个数都增加 1。

规律与证明

两种操作中：

• 第一种操作一定优于第二种操作。

• 第一种操作的次数极少，因为仅当 $t \in \left [ 2,\log_2 (n)\right ]$ 时 $t + 2^t \leq n$。又因为 $1 \leq n \leq 10^{18}$，所以 $t$ 仅能取 $\left [ 2,\log_2 (10^{18})\right ] \approx \left [ 2,60\right ]$。次数很少，可以近似地当作常数。恰好，按照上文的分组，每组中由第一种操作 $t + 2^t$ 得到的值有且仅有一个，并且出现在第一个循环的最后一个数中。

• 绝大部分操作都为第二种操作，而第二种操作中的 $\lfloor\log_2(t-1)\rfloor$ 很明显可以分段。按照上文的分组，每个组中 $\lfloor\log_2(t-1)\rfloor$ 是固定的，即对于第 $k$ 组中的任意 $t$，$\lfloor\log_2(t-1)\rfloor = k$。

这就说明了为什么第 $k$ 组的循环是 $k$ 个数一轮，并且每个数逐轮增加。

实现部分

部分打表

由于操作 1 的次数很少并且 $t$ 仅能取 $\left [ 2,60\right ]$，所以我们可以通过手工计算的方法，把 $t$ 在 $\left [ 2,60\right ]$ 范围内时 $f(t)$ 的值都计算出来。详见程序。

预处理

我们需要预处理以下几个值，方便计算。

• $v_{k,j}$ 表示第 $k$ 组第一个循环中的第 j 个的值。
• $sum_k$ 表示第 $k$ 组第一个循环数字的总和。
• $rs_k$ 表示第 $k$ 组中所有数的总和。

这三个值我们需要按照顺序计算，数组 $v_k$ 可以根据 $v_{k-1}$ 和第 k 个数字在打好的表中的答案求出。 其它两个根据 $v$ 计算，比较简单。

分段查询

对于题目给出的 $n$，我们分为 $\lceil\log_2(n)\rceil-1$ 组。前面完全包含的 $n-1$ 组，直接在答案上用 $rs_k$ 累加即可。最后一组用和预处理类似的方法计算。

代码

有点丑，前面没看懂的可以通过代码尝试理解。

效率还可以是目前最优解。

// Author: chenly8128
// Created: 2024-08-26 15:05:29

#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
int kase;
long long n;
vector <long long> v[64];
long long sum[64];
long long rs[64];
const long long l[70] = {0,0,0,0,1,2,1,3,2,4,3,1,5,4,2,6,5,3,7,6,2,4,8,7,3,5,9,8,4,6,10,9,5,7,11,10,6,3,8,12,11,7,4,9,13,12,8,5,10,14,13,9,6,11,15,14,10,7,12,16,15,11,8,13,17};
int main (void) {
	v[1].resize(1,0);
	sum[1] = 0;rs[1] = 1;
	for (int i = 2;i <= 61;i++) {
		v[i].clear();int t = 0;
		for (int j = (1l<<(i-1))%(i-1);t < i-1;j = (j+1)%(i-1),t++) {
			v[i].push_back((v[i-1][j]+((1l<<(i-1))-j+t)/(i-1))%mod);
			sum[i] = (sum[i]+v[i][t])%mod;
		}
		v[i].push_back(l[i]+1);
		sum[i] += l[i]+1;
		rs[i] = sum[i] * ((1l<<i)/i%mod) % mod;
		long long k = ((1l<<i)/i)%mod;
		rs[i] = (rs[i]+k*(k-1)/2%mod*i)%mod;
		for (int j = 0;j < (1l<<i)%i;j++)
			rs[i] = (rs[i] + v[i][j] + k)% mod;
		rs[i] %= mod;
	}
	scanf ("%d",&kase);
	while (kase--) {
		scanf ("%lld",&n);
		if (n <= 3) {
			puts ("0");
			continue;
		}
		long long res = 0;int i;
		for (i = 1;1l<<(i+1) < n;i++) {
			res = (res+rs[i])%mod;
		}
		res %= mod;
		long long k = (n-(1l<<i))/i%mod;
		res = (res + sum[i] * k % mod);
		res = (res+(k-1)*k/2%mod*i)%mod;
		for (int j = 0;j < (n-(1l<<i))%i;j++)
			res = (res+v[i][j]+k)%mod;
		res %= mod;
		printf ("%lld\n",res);
	}
	return 0;
}