自动搬运

查看原文

来自洛谷，原作者为

	Inv_day_in_R > 强制在线：2025年8月24日21时18分 <

搬运于2025-08-24 23:03:08，当前版本为作者最后更新于2024-11-21 21:03:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

本题是 P2365 的强化版，先思考 P2365 怎么做。

我们用 $dp_i$ 来表示 $i+1$ 重新启动机器，区间 $1$ 到 $i$ 之间费用的最小值。不难想到每次机器启动都会给之后的所有机器都带来 $s$ 的时间，则启动代价为 $s\sum\limits_{k=i+1}^{n}C_k$，设上一次由 $dp_j$ 转移来，$j+1$ 到 $i$ 之间运行代价为 $\sum\limits_{k=j+1}^iC_k\sum\limits_{k=1}^iT_k$。

这里使用前缀和优化，最终，得到如下的转移方程：

$$dp_i=\min\limits_{0<j<i}(dp_j+(C_i-C_j)T_i+(C_n-C_j)s) $$

时间复杂度 $O(n^2)$，可以通过 P2365。

接下来考虑本题的斜率优化。斜率优化需要对原方程进行变形，先省略 $\min$，相当于求 $dp_i=dp_j+(C_i-C_j)T_i+(C_n-C_j)s$ 的最小值。 接下来如下进行变形：

$$dp_i=dp_j+C_iT_i-C_jT_i+C_ns-C_js\\ dp_j=dp_i-C_iT_i+C_jT_i-C_ns+C_js\\ dp_j=(T_i+s)C_j+(dp_i-C_iT_i-C_ns) $$

化成这个形式之后，发现像一个一次函数，于是以 $C_j$ 为 $x$ 轴，$dp_j$ 为 $y$ 轴建立平面直角坐标系，平面上第 $j$ 个点为 $(C_j,dp_j)$，而每次转移时的 $T_i+s$ 与 $-C_iT_i-C_ns$ 都是一个常量，要使 $dp_i$ 最小也就是在前 $i-1$ 个点中选出过这个点，斜率为定值的直线中截距最小的那个。

不难发现，答案必然在原点集的一个右下凸包上：

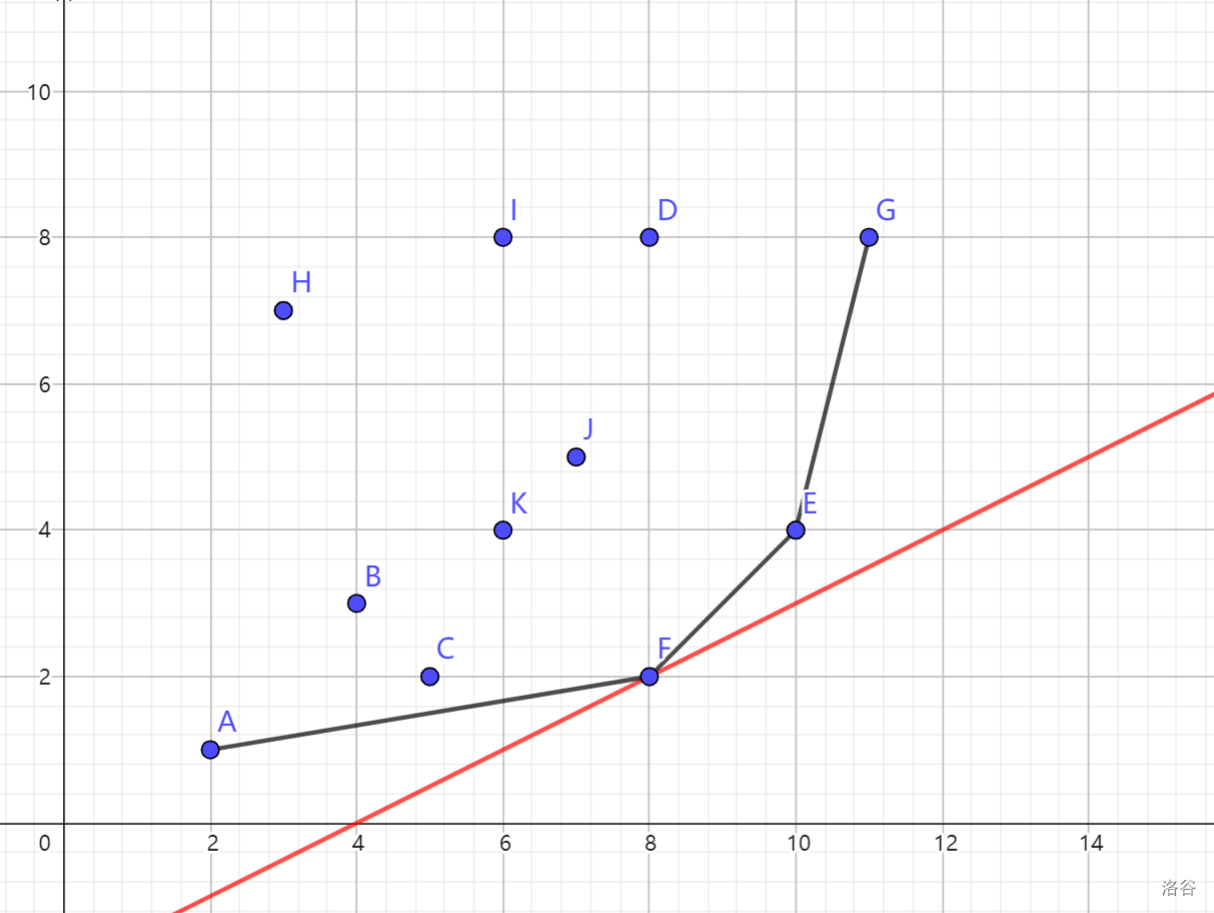
考虑如何动态维护凸包。$C_i$ 单调递增，所以新加入的点必然在右边。

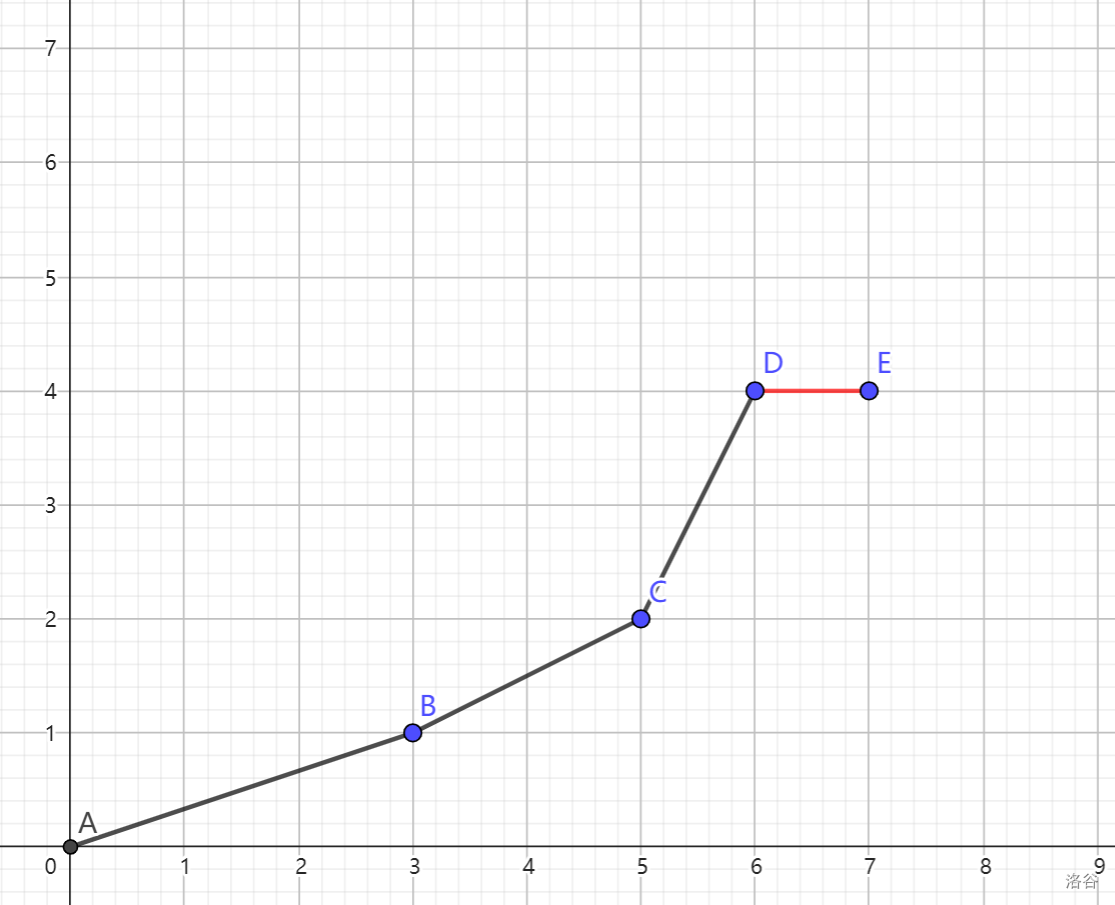
如上图，CD 斜率大于 DE 斜率，所以 D 被删除，然后再看 BC 与 CE。

查询时二分即可。 代码如下：

#include<iostream>
#define int long long 
using namespace std;
int n,s,t[300010],c[300010],f[300010];
int q[300010];
main(){
    cin>>n>>s;
    for(int i=1;i<=n;i++){
        cin>>t[i]>>c[i];
        t[i]+=t[i-1];
        c[i]+=c[i-1];
    }
    int hh=0,tt=0;
    q[0]=0;
    for(int i=1;i<=n;i++){
        int l=hh,r=tt;
        while(l<r){
            int mid=l+r>>1;
            if((__int128)(t[i]+s)*(c[q[mid+1]]-c[q[mid]])<(__int128)(f[q[mid+1]]-f[q[mid]]))r=mid;
            else l=mid+1;
        }
        int j=q[r];
        f[i]=f[j]+c[i]*t[i]-c[j]*t[i]+c[n]*s-c[j]*s;
        while(hh<tt&&(__int128)(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])<=(__int128)(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]]))tt--;
        q[++tt]=i;
    }
    cout<<f[n];
}

这个代码还能过 P5785。