自动搬运

查看原文

来自洛谷，原作者为

	wjyppm1403 我一直在试图撼动着 我曾要攀登的巍然山峦

搬运于2025-08-24 23:02:59，当前版本为作者最后更新于2025-03-13 22:14:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目大意：

给定 $n$ 个平台，第 $i$ 个平台的高度为 $i$ ，其左右端点为 $L_i,R_i$。现在你在第 $n$ 个平台上，横坐标为 $S$，可以选择在平台的左端点或右端点跳到下一个平台。你需要设计一个移动方案使得移动到 $(0,0)$ 点时水平移动距离最小。输出最小水平移动距离。

下面我们将栅栏用“平台”一词来代替。

根据题意，能够发现奶牛跑到第 $i$ 个平台时有 2 种决策，分别是向左走到左端点和向右走到右端点，设 $f[i][0/1]$ 表示当前到达第 $i$ 个平台，向左走到左端点（即 0）或向右走到右端点（即 1）的累计距离最小值。

如果枚举从哪块模板跳过来复杂度可能会退化，我们可以考虑递推的思想，枚举下面的跳板 $j$，分别从左右端点枚举，只要枚举到第一个能够跳到的就结束枚举（你又不能穿过去这个跳板）。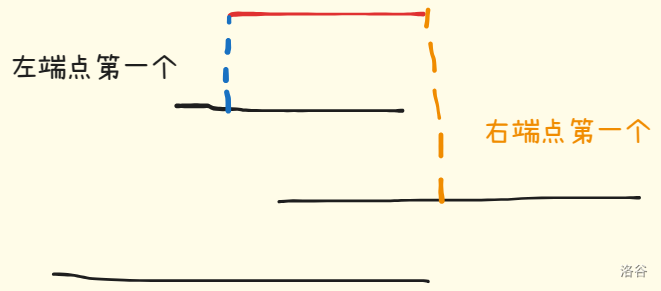

转移方程如下，其中 $j$ 表示左端点往下走走到的第一个平台，$k$ 表示右端点往下走走到的第一个平台：

$$f[j][0]=\min\limits_{L_j\le L_i \le R_j}f[i][0]+|L_i-L_j| \\ f[j][1]=\min\limits_{L_j\le L_i \le R_j}f[i][0]+|L_i-R_j| $$$$f[k][0]=\min\limits_{L_k\le R_i \le R_k}f[i][1]+|R_i-L_k| \\ f[k][1]=\min\limits_{L_k\le R_i \le R_k}f[i][1]+|R_i-R_k| $$

初始化 $f[n][0]=|s-L_n|, f[n][1]=|R_n-s|$，其余全部为正无穷。

这样的时间复杂度是 $O(n^2)$，不能通过本题。

观察转移方程，我们发现瓶颈就在于枚举一个在区间范围的合法值 $j,k$。要查询的是第一个，又是区间查询。我们可以使用线段树来优化。

我们可以从小到大枚举，每一次我们查询左端点被下方的哪一个点覆盖，右端点同理，记录下来，查询完后我们对 $[L_i,R_i]$ 进行区间赋值，赋值为 $i$。这样我们查询的值刚好就是上面要求的往下走第一个值，转移方程同上，做法是等价的只不过用线段树加快了查询。

时间复杂度为 $O(n \log n)$，瓶颈在插入与查询。

本题的坐标有负值，可以考虑离散化或都加上一个偏移量，这里采用后者方法。注意区间覆盖用懒标记优化复杂度，线段树不应当有 pushup，因为这里维护的是单独区间颜色信息（当然也可以用珂朵莉树，但是复杂度不一定了）。

代码如下：

#include <bits/stdc++.h>
#define ls p << 1
#define rs p << 1 | 1
#define getn(x) (x + 100001) // 坐标偏移，将负坐标转换为正数方便处理
using namespace std;
constexpr int MN = 2e6 + 15;
int f[MN][2], lc[MN], rc[MN], n, s;
// lc，rc为记录的编号
struct zhalan {
    int l, r;
} zl[MN];

struct segtree {
    int l, r, val, cov;
} t[MN << 2];


void pushdown(int p) {
    if (t[p].cov) {
        t[ls].val = t[rs].val = t[ls].cov = t[rs].cov = t[p].cov;
        t[p].cov = 0;
    }
}

void build(int p, int l, int r) {
    t[p].l = l;
    t[p].r = r;
    if (l == r) return;
    int mid = l + r >> 1;
    build(ls, l, mid);
    build(rs, mid + 1, r);
}

void cover(int p, int fl, int fr, int k) {
    if (t[p].l >= fl && t[p].r <= fr) {
        t[p].cov = t[p].val = k;
        return;
    }
    pushdown(p);
    int mid = (t[p].l + t[p].r) >> 1;
    if (mid >= fl) cover(ls, fl, fr, k);
    if (mid < fr) cover(rs, fl, fr, k);
}


int query(int p, int pos) {
    if (t[p].l == t[p].r) return t[p].val;
    pushdown(p);
    int mid = (t[p].l + t[p].r) >> 1;
    return pos <= mid ? query(ls, pos) : query(rs, pos);
}

int main() {
    memset(f, 0x3f, sizeof(f)); // 初始化为极大值
    build(1, 1, 2e6);
    zl[0].l = zl[0].r = getn(0); //注意这里是getn(0)! 原点也要偏移！
    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> a >> b;
        zl[i].l = getn(a);//偏移l，r
        zl[i].r = getn(b);
        lc[i] = query(1, zl[i].l); // 查询当前平台i的左端点下方第一个平台编号
        rc[i] = query(1, zl[i].r); // 查询当前平台i的右端点下方第一个平台编号
        cover(1, zl[i].l, zl[i].r, i); // 将区间[zl[i].l, zl[i].r]标记为平台i
    }

    f[n][0] = abs(getn(s) - zl[n].l);
    f[n][1] = abs(zl[n].r - getn(s));

    for (int i = n; i >= 1; i--) {// 递推，启动！
        // 从当前平台i的左端点跳到下方平台lc[i]的左右端点
        f[lc[i]][0] = min(f[lc[i]][0], f[i][0] + abs(zl[i].l - zl[lc[i]].l));
        f[lc[i]][1] = min(f[lc[i]][1], f[i][0] + abs(zl[i].l - zl[lc[i]].r));
        // 从当前平台i的右端点跳到下方平台rc[i]的左右端点
        f[rc[i]][0] = min(f[rc[i]][0], f[i][1] + abs(zl[i].r - zl[rc[i]].l));
        f[rc[i]][1] = min(f[rc[i]][1], f[i][1] + abs(zl[i].r - zl[rc[i]].r));
    }
    cout << f[0][0]; // 这里也可以是f[0][1]
    return 0;
}