自动搬运

查看原文

来自洛谷，原作者为

	Graph Reject || 错的不是我，而是这个世界

搬运于2025-08-24 23:02:39，当前版本为作者最后更新于2024-11-20 17:07:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

Update

• 边权的设定中，第二条将打错的 $s$ 改为 $p$，并优化码风和 $\LaTeX$。

---

写圆方树板子，纠结了好久，用了一下午才把它弄懂，写篇题解回顾一下。

原题，双倍经验。

题意

给一棵仙人掌，每次询问两点之间的最短距离。

题解

我们讲讲如何发明圆方树的人怎么想到的。

首先，如果不考虑环的边权，那么缩点双连通分量，LCA 即可。

那么现在有环的边权，我们不可能像基环树那样对每个点进行操作，因为一条路径上如果全是环，那么复杂度就爆炸了。

于是，我们考虑越过一个环如何处理。

越过一个环，有两种情况，我们分别考虑。

first

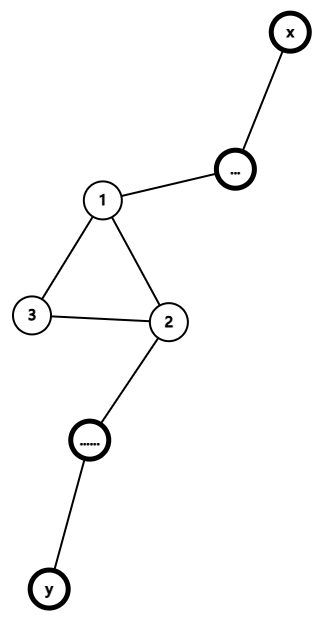
注：我们假设 $dep_x<dep_1<dep_y$，$dep_a$ 代表 $a$ 在搜索树的深度。

这种情况我们只需要知道环上的点到环上深度最小的点的距离，我们设深度最小的点是 $p$。

那么我们可以建一个虚点（也就是方点，设其为 $s$），边权有如下设定：

• $s \leftrightarrow p$ 的边边权为 $0$。
• $i \ne p,s \leftrightarrow i$ 的边权为环上 $i$ 和 $p$ 的距离的最小值。
• 同时去除环上的边。

这样我们就可以实现任意 $i \ne p$，$i \to p$ 的路径最小值等于 $i$ 和 $p$ 树上两点之间的距离了。

second

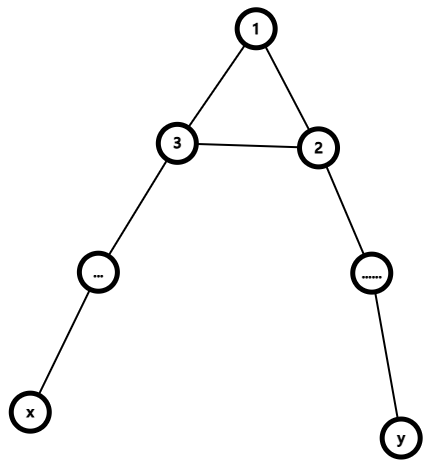
注：我们设 $dep_1 < dep_x$，$dep_1 <dep_y$。

这种情况对于刚才的建树就失效了，因为刚才只统计了每个节点到深度最小的节点的距离。

但是，我们会发现一个很好的性质：这种情况只会在他们的最近公共祖先处出现一次。

于是我们就可以找到它们最短路径上最近公共祖先“下面”的两个点，我们设它们为 $x_0,y_0$，$x \leftrightarrow x_0$ 和 $y \leftrightarrow y_0$ 的距离可以 $O(1)$ 求，接下来转化为求 $x_0 \leftrightarrow y_0$ 的距离。

很简单，预处理每个环的前缀和，找到他们取个最小值即可。

总结

Tarjan 算法缩点是 $O(n)$ 的，建圆方树是 $O(n)$ 的。

LCA 我写的树剖，预处理 $O(n)$，查询 $O(\log n)$。

综上，时间复杂度为 $O(n+m+q\log n)$。

如果使用离线 Tarjan 求 LCA，可以做到优秀的线性复杂度。

关于代码实现

我们可以在 Tarjan 是顺便把圆方树建出来，但是有些复杂，我们结合重要代码（对于一个环建圆方树）看一看。（可以先看后面的代码部分，这里只是突出重点部分）

void help(int x,int y,int val) //val 是非树边边权 
{
	int cur=y,lst=val;
	while(cur!=x)
	{
		sum[cur]+=lst;
		sum[fa[cur]]+=sum[cur];
		lst=vval[cur];
		cur=fa[cur];
	}
	int sq=++ext;
	sum[sq]=sum[x]+lst; // 将所有边权放在方点上 
	sum[x]=0; // 方便后面处理 
	cur=y;
	while(cur!=fa[x])
	{
		int val=min(sum[cur],sum[sq]-sum[cur]); //再来一遍记录边权 
		Tree::add(cur,sq,val);
		cur=fa[cur];
	}
	return ;
}

我们注意到有一行 _tree.sum[x]=0，我们解读一下。

$x$ 是环深度最小的点，目前已经把 $x$ 的子树遍历完。

后面代码的 $\min$ 实际上要减一个 _tree.sum[x]，由于它是 $0$，所以忽略不计。

询问如果最近公共祖先在环内，那么上文中 $x_0,y_0$ 一定不是 $x$，因为 $x$ 的深度比方点小。

如果两个环有交点，那么交点在搜索树上必然会是两个环深度最小的节点之一。

证明比较简单，因为我们是按 DFS 序来确定深度的，访问到的第一个节点就是深度最小的，其余的点深度都比他大，因为其余点后遍历到。

同时，我们会优先处理最小深度较大的环，所以，两个环相交，交点只在一个环中有意义，对于这个交点在深度最小的那一个环，我们会先将它赋值成没有意义的 $0$，保证后面前缀和的累加不会出问题。

代码

码风真的丑。

#include<bits/stdc++.h>
using namespace std;
#define int long long 

const int N=1e5+5;
int n,m,q,ext,fa[N];
class eg
{
public:
	int to,w;
};

namespace Tree
{

vector<eg>nbr[N];
int dis[N],sum[N],siz[N],hvy[N],sg[N],dep[N],fat[N];

void add(int x,int y,int w)
{
	nbr[x].push_back({y,w});
	nbr[y].push_back({x,w});
	return ;
}

void init(int cur,int fa)
{
	dep[cur]=dep[fa]+1;
	fat[cur]=fa;
	siz[cur]=1;
	for(auto dat:nbr[cur])
	{
		int nxt=dat.to,w=dat.w;
		if(nxt==fa)
			continue;
		dis[nxt]=dis[cur]+w;
		init(nxt,cur);
		siz[cur]+=siz[nxt];
		if(siz[nxt]>siz[hvy[cur]])
			hvy[cur]=nxt;
	}
	return ;
}

void dfs(int cur)
{
	if(hvy[fat[cur]]==cur)
		sg[cur]=sg[fat[cur]];
	else
		sg[cur]=cur;
	for(auto dat:nbr[cur])
		if(dat.to!=fat[cur])
			dfs(dat.to);
	return ;
}

int lca(int x,int y)
{
	while(sg[x]!=sg[y])
	{
		if(dep[sg[x]]<dep[sg[y]])
			x^=y^=x^=y;
		x=fat[sg[x]];
	}
	if(dep[x]>dep[y])
		x^=y^=x^=y;
	return x; 
}

int findson(int x,int zx)
{
	while(dep[x]-1>dep[zx])
	{
		x=sg[x];
		if(fat[x]==zx)
			return x;
		x=fat[x];
	}
	if(fat[x]==zx)
		return x;
	return hvy[zx];
}

int query(int x,int y)
{
	int pos=lca(x,y);
	if(pos<=n)
		return dis[x]+dis[y]-2*dis[pos];
	else //方点 
	{
		int sx=findson(x,pos),sy=findson(y,pos);
		int now=dis[x]+dis[y]-dis[sx]-dis[sy];
		if(sum[sx]>sum[sy])
			sx^=sy^=sx^=sy;
		int val=sum[sy]-sum[sx];
		return now+min(val,sum[pos]-val);
	}
}}

namespace Graph
{
using Tree::sum;

int dfn[N],low[N],tot,dep[N],vval[N];
vector<eg>nbr[N];

void build()
{
	for(int i=1;i<=m;i++)
	{
		int x,y,w;
		cin>>x>>y>>w;
		nbr[x].push_back({y,w});
		nbr[y].push_back({x,w});
	}
	return ;
}

void help(int x,int y,int val) //val 是非树边边权 
{
	int cur=y,lst=val;
	while(cur!=x)
	{
		sum[cur]+=lst;
		sum[fa[cur]]+=sum[cur];
		lst=vval[cur];
		cur=fa[cur];
	}
	int sq=++ext;
	sum[sq]=sum[x]+lst; // 将所有边权放在方点上 
	sum[x]=0; // 方便后面处理 
	cur=y;
	while(cur!=fa[x])
	{
		int val=min(sum[cur],sum[sq]-sum[cur]); //再来一遍记录边权 
		Tree::add(cur,sq,val);
		cur=fa[cur];
	}
	return ;
}

void Tarjan(int cur,int fa)
{
	::fa[cur]=fa;
	dep[cur]=dep[fa]+1;
	dfn[cur]=low[cur]=++tot;
	for(auto dat:nbr[cur])
	{
		int nxt=dat.to,w=dat.w;
		if(nxt==fa)
			continue;
		if(dfn[nxt]==0)
		{
			Tarjan(nxt,cur);
			vval[nxt]=w; //把边权放到深度较深的点上 
			low[cur]=min(low[cur],low[nxt]);
		}
		else
			low[cur]=min(low[cur],dfn[nxt]);
		if(low[nxt]>dfn[cur]) //点双连通可以有等于，这里不行，因为是圆点的连边，nxt 有反祖边到 cur 同样形成环 
			Tree::add(cur,nxt,w);
	}
	for(auto dat:nbr[cur])
	{
		int nxt=dat.to,w=dat.w;
		if(nxt==fa)
			continue;
		if(::fa[nxt]!=cur&&dep[cur]<dep[nxt]) //找到非树边 
			help(cur,nxt,w);
	}
	return ;
}}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n>>m>>q;
	ext=n;
	Graph::build();
	Graph::Tarjan(1,0); //建圆方树 
	Tree::init(1,0); 
	Tree::dfs(1); //Tree chain split
	while(q--)
	{
		int x,y;
		cin>>x>>y;
		cout<<Tree::query(x,y)<<"\n";
	}
	return 0;
}

---

欢迎提问。