自动搬运

查看原文

来自洛谷，原作者为

	tjtdrxxz 要是把博士抬去寝室，会不会被人误会啊？干脆就这样子放着好了......？

搬运于2025-08-24 23:02:38，当前版本为作者最后更新于2024-09-13 19:30:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先，我们可以快速的想出暴力：$O (nm)$ 暴力判断。

但很明显，因为 $n \le 10^5, m \le 2 \times 10^5$，所以暴力是不可行的。

根据题面，我们可以看出最开始的主猪主边 black 组成了一棵树，所以我们切掉任意一边都可以是他被分成两个连通块。然后就是附加边 red：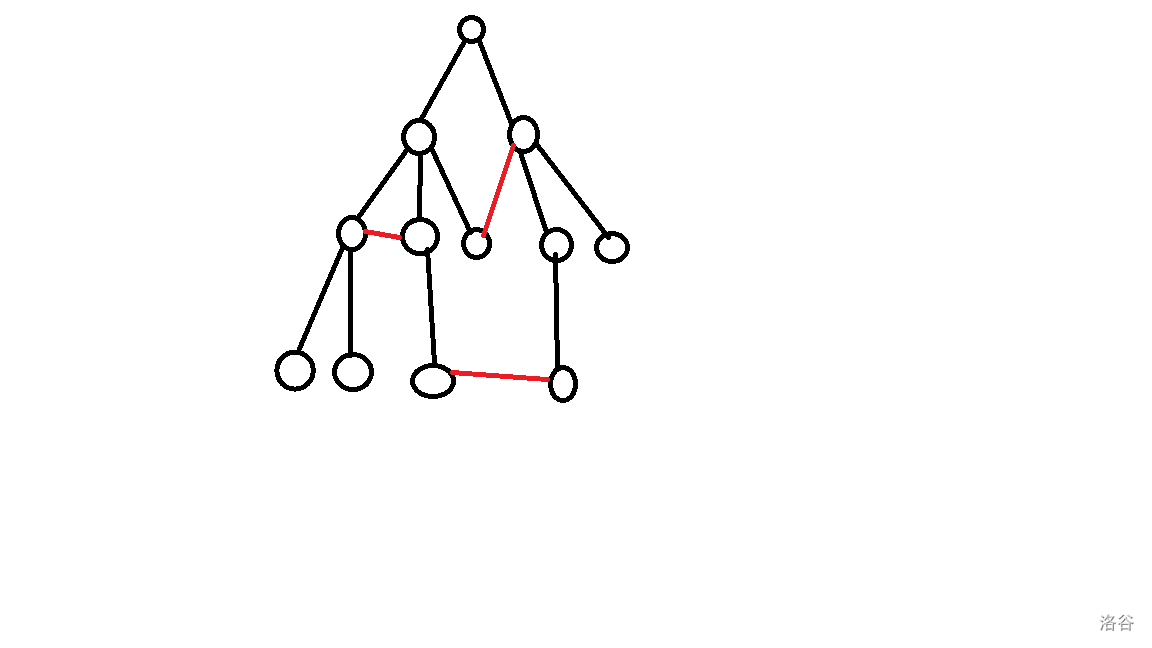

根据图我们可以发现，若一点下的子树与外面有一条附加边，那么我们的方案数就可以加上该子树下的边的的数量，当然，如果该子树没有一条与外面相连的边，则我们不管 kill 哪条边图都会不连通，方案数就是所有附加边的数量。

但是直接统计复杂度又会因为比较暴力的修改退化成 $O (nm)$，很显然，对于每条附加边，该边做出的贡献一定是在改变的两个节点的 LCA 的子树下。

因为在该子树下，一定存在一个子树有与外面相连的附加边。

所以继续树状数组的思路，我们直接在树上差分，把 $a_u + 1$, $a_v + 1$, $a _ { LCA (u, v) } - 2$,最后统计答案时，我们直接遍历整棵树，把每个点的答案统出来，最后遍历 $2$ ~ $n$把各个点的答案加起来就 ok 了。

code

# include "bits/stdc++.h"
using namespace std;
int f[500012][52];
vector <int> e[500012];
int dp[500012], q, n, m;
void find (int x)
{
	for (int i = 0; i < e[x].size (); i ++)
	{
		if (e[x][i] != f[x][0])
		{
			dp[e[x][i]] = dp[x] + 1;
			f[e[x][i]][0] = x;
			find (e[x][i]);
		}
	}
}
int LCA (int x, int y)
{
	if (dp[x] < dp[y]) swap (x, y);
	for (int i = 26; i >= 0; i --)
	{
		if (dp[x] - (1 << i) >= dp[y])
		{
			x = f[x][i];
		}
		if (x == y)
		{
			return x;
		}
	}
	for (int i = 26; i >= 0; i --)
	{
		if (f[x][i] != f[y][i])
		{
			x = f[x][i];
			y = f[y][i];
		}
	}
	return f[x][0];
}
int ans[100012], out, num[100012];
void dfs (int u, int fa)
{
	num[u] = ans[u];
	for (int i = 0, v; i < e[u].size (); i ++)
	{
		v = e[u][i];
		if (v == fa) continue;
		dfs (v, u);
		num[u] += num[v];
	}
}
int main ()
{
	ios :: sync_with_stdio (0);
	cin.tie (0), cout.tie (0);
	cin >> n >> m;
	for (int i = 1; i < n; i ++)
	{
		int u, v;
		cin >> u >> v;
		e[u].push_back (v);
		e[v].push_back (u);
	}
	q = 1;
	find (q);
	for (int j = 1; (1 << j) <= n; j ++)
	for (int i = 1; i <= n; i ++)
	{
		f[i][j] = f[f[i][j - 1]][j - 1];
	}
	for (int i = 1; i <= m; i ++)
	{
		int u, v;
		cin >> u >> v;
		int lca = LCA (u, v);
		ans[u] += 1;
		ans[v] += 1;
		ans[lca] -= 2;
	}
	dfs (q, 0);
	out = 0;
	for (int i = 2; i <= n; i ++) out += (num[i] == 0 ? m : (num[i] == 1));
	cout << out << endl;
}