自动搬运

查看原文

来自洛谷，原作者为

	xtx1092515503 Mathematics compares the most diverse phenomena, and discovers the secret analogies which unite them. @Joseph Fourier

搬运于2025-08-24 23:02:34，当前版本为作者最后更新于2024-10-31 16:51:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

作为常用 ID 前缀是 10925 的用户，那就交一份 P10925 的题解罢。

时隔约十个月的洛谷 submission。

首先考虑 $n$ 为偶数的场合。显然，我们可以将这个“斜正方形”拆成四个象限，求出一个象限的最优解，然后将其翻转复制到其它象限里。因此我们只需考虑一个象限的问题。以下是这个模型的抽象版本：

• 从左往右第 $i$ 列有 $n-i+1$ 个方格；第 $x$ 列第 $y$ 个方块记作 $(x,y)$。

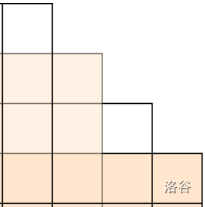
即这个模式。

现在，贪心地，我们肯定会把矩形的角放到某个 $(i,n-i+1)$ 格处。

直接思考如何放矩形并不是一个好选择，我们可以反向考虑：应该如何安排那些“不存在矩形顶点”的格子，使得未被矩形覆盖的格子数尽量少？

令 $s_i\in\{0,1\}$ 表示 $(i,n-i+1)$ 不是/是 矩形的顶点，则 $s$ 是一个长度为 $n$ 的零一串。易知：$s$ 中每段极长 $0$ 子串，令其长度为 $l$，会贡献 $\dfrac{l(l+1)}2$ 个未被覆盖的格子。通过调整，易知任两个极长 $0$ 子串长度 $l_1,l_2$ 必有 $|l_1-l_2|\leq1$，否则我们可以令大者减一、小者加一，则未覆盖格子数严格减。

因此算法就很明了了：$s$ 中恰有 $b=n-m$ 个 $0$，其被分成 $m+1$ 段。于是造出 $b\bmod(m+1)$ 个长度为 $\left\lfloor\dfrac b{m+1}\right\rfloor+1$ 的 $0$ 段，$m+1-[b\bmod(m+1)]$ 个长度为 $\left\lfloor\dfrac b{m+1}\right\rfloor$ 的 $0$ 段，即可最小化总未覆盖格子数。

然后考虑 $n$ 为奇数的场合。此时与偶数唯一的区别就是“坐标轴”上有一些格子，如果简单粗暴地拆分的话，这些格子的贡献要么被重复计算，要么被不恰当地忽略了。

为了减少脑力劳动，我们采取最暴力的方法：易发现坐标轴附近的 $0$ 段长度虽然有可能既非 $\left\lfloor\dfrac b{m+1}\right\rfloor$ 又非 $\left\lfloor\dfrac b{m+1}\right\rfloor+1$，但它总归不会离太远，否则调整即可。因此我们手动在 $\left\lfloor\dfrac b{m+1}\right\rfloor\pm3$ 的范围内枚举这两段的长度，然后中间的部分就是一个朴素的偶数场合了。

• 这种一言不合就枚举的方式我认为是有效减少分类讨论题脑力劳动以及代码量的高效方式。

void mina(){
	scanf("%d%d",&n,&m),res=0;
	if(!(n&1)){
		n>>=1;
		int b=n-m;
		int l1=b/(m+1),n2=b%(m+1),l2=l1+1,n1=(m+1)-n2;
//		printf("%d %d %d %d\n",l1,n1,l2,n2);
		res=2ll*n*(n+1)-2ll*l1*(l1+1)*n1-2ll*l2*(l2+1)*n2;
	}else{
		n>>=1;
		int b=n+1-m,l=b/(m+1);
		for(int i=l-3;i<=l+3;i++)for(int j=l-3;j<=l+3;j++)
			if(i>=0&&j>=0&&i+j<=b){
				if(m==1){
					if(i+j==b)
						res=max(res,2ll*n*(n+1)+1-2ll*i*i-2ll*j*j);
				}else{
					int B=b-i-j;
					int l1=B/(m-1),n2=B%(m-1),l2=l1+1,n1=(m-1)-n2;
					res=max(res,2ll*n*(n+1)+1-2ll*l1*(l1+1)*n1-2ll*l2*(l2+1)*n2-2ll*i*i-2ll*j*j);
				}
			}
	}
	printf("%lld\n",res);
}