自动搬运

查看原文

来自洛谷，原作者为

	_std_O2 FQBC

搬运于2025-08-24 23:02:27，当前版本为作者最后更新于2024-09-16 15:52:29，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P10911 题解

反转函数的写法

首先按题意把一个十进制数转为二进制，这里我们可以用短除法来解决。

int d[50],now=0;;
while(x>=1){
  d[++now]=x%2;
  x/=2;
}

然后我们可以使用 reverse() 函数来反转这个 d 数组。

reverse(d+1,d+now+1);

这个函数的使用方法就像 sort() 一样，此处不再赘述。

最后把这个二进制数再转回十进制。

int sum=0;
for(int i=1;i<=now;i++){
	if(d[i]) sum+=mem[i-1];
}

思路分析

我的第一个想法就时贪心，但又不能找到一个具有普遍性的贪心策略，于是想到了动态规划。

dp 数组的定义

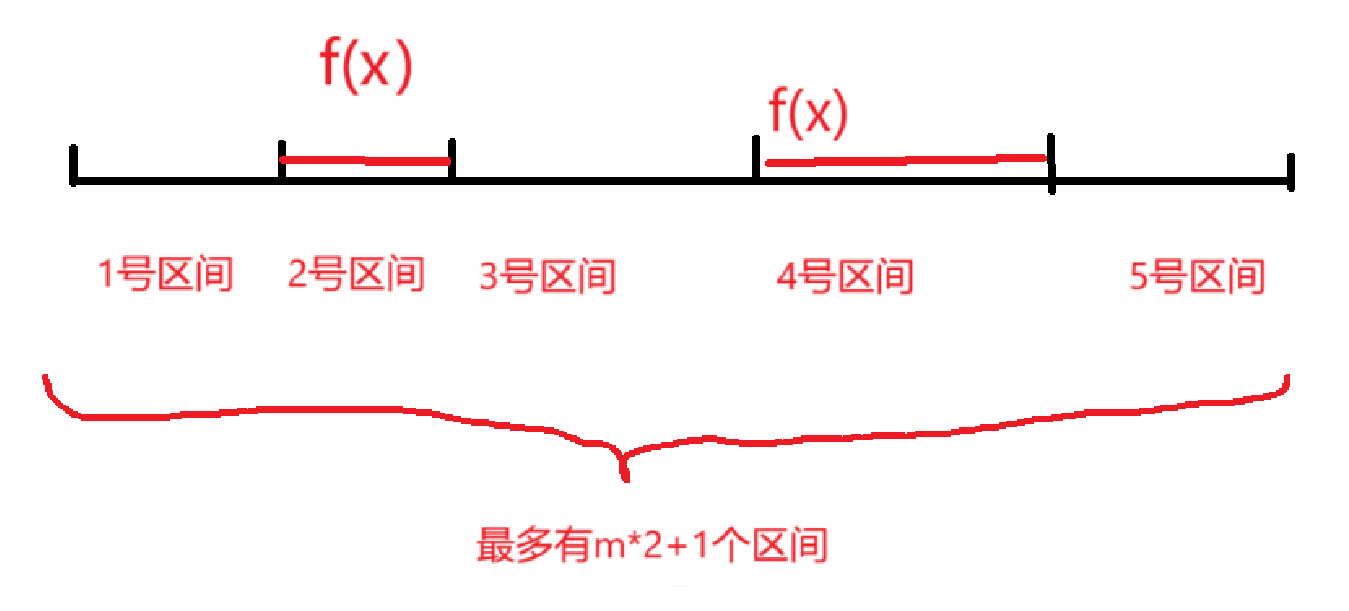
先来看一下下面这张图片。

因为题目中提到了区间，所以我们先把这些区间画下来。

图中带有 $f(x)$ 的区间为经过反转的区间，反之其他就是没有经过反转的。

观察发现，偶数个的区间都要经过反转。

因为经过反转的区间的两旁肯定是没有经过反转的区间。

当然，区间的长度可能为 0。

所以我们定义 $dp_{i,j}$ 是以 $a_i$ 结尾的，在第 $j$ 个区间的最大和。

状态转移方程与目标

可推出：

$$dp_{i,j}=\max(dp_{i-1,j}+a_i,dp_{i-1,j-1}+a_i)(j \bmod 2=1)\\ dp_{i,j}=\max(dp_{i-1,j}+rev_i,dp_{i-1,j-1}+rev_i)(j \bmod 2=0) $$

解释：

对于 $dp_{i,j}$ 可以继续保持在第 $j$ 个区间上，同时也可以从第 $j-1$ 个区间（上一个区间）转移过来。（代表开始反转或结束反转）

如果不能理解，可以再仔细想想 $dp$ 数组的定义。

可推出答案 $\max\limits_{i=1}^{2m+1}f_{n,i}$。

解释：

最多有 $2m+1$ 个区间但不代表取到最大和的答案已经在第 $2m+1$ 个区间，甚至有可能答案就没有经过反转的区间或者只经过了几个。所以答案并不是 $dp_{n,2m+1}$。

代码

#include<iostream>
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3005;
int a[N],dp[N][N],rev[N];
int f(int x){//反转函数
	int d[50],now=0;
	while(x>=1){
		d[++now]=x%2;
		x>>=1;
	}
	reverse(d+1,d+now+1);
	int sum=0;
	for(int i=1;i<=now;i++)  if(d[i]) sum+=1<<i-1;
	return sum;
}
signed main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=n;i++) rev[i]=f(a[i]);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=2*m+1;j++){
			int flag=a[i];
			if(j%2==0) flag=rev[i];
			dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+flag;//核心
		}
	}
	int ans=-1;
	for(int i=1;i<=2*m+1;i++){
		ans=max(ans,dp[n][i]);
	}
	cout<<ans;
}

都写的这么全了，给个赞再走吧 QwQ。