自动搬运

查看原文

来自洛谷，原作者为

	VitrelosTia What you want, What you do ?

搬运于2025-08-24 21:20:49，当前版本为作者最后更新于2023-04-09 22:07:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

题解区大多使用的都是时间复杂度 $O(n^2)$ 的算法，唯一使用二分查找的 $O(n \log n)$ 做法的被 hack 了，所以写一篇二分查找 $O(n \log n)$ 复杂度的题解。

upd(2025.4.5)：这篇题解是我远古时期写的，当时只是想介绍一种没什么用的解法，因为一些比较神秘的原因现在是第一篇，所以我打算新增一些内容。

题意分析

题目中要求的“合唱队形”满足的要求其实就是：$t_1, t_2, t_3, \dots, t_i$ 成上升序列，$t_i, t_{i + 1}, t_{i + 2}, \dots, t_n$ 成下降序列。题目中要求算出最少出列人数，其实就是要求哪个 $i$ 能使得以 $a_i$ 为结尾的最长上升子序列和最长下降子序列之和最大。

做法

这道题想要用 $O(n \log n)$ 的复杂度做，首先要用 $O(n \log n)$ 求出最长上升子序列（下面简称 LIS）的长度。

dp 的做法我放在后面了，有需要的朋友可以翻到后面看。

$O(n \log n)$ 求 LIS 长度

在 $O(n^2)$ 的做法中，求 LIS 长度的做法需要通过枚举两个数，假如是满足上升的，就将长度更新为原长度和新长度加一的最大值。通过这个朴素做法我们可以发现，以当前数结尾的 LIS 长度是否能达到 $k$，取决于它是否能比一个长度为 $k - 1$ 的序列的结尾数大。我们可以观察一组数据。

该组数据中，我们记下以每个数结尾的 LIS 长度，由于上面所讲的，对于长度为 $k$ 的数据，我们只需要关注结尾数最小的，因为这代表它有可能产生的长度为 $k + 1$ 的 LIS 长度最多。于是我们可以去掉一些数据。

还是上面的道理，我们把还留着的数据的上方的数放到一个数轴上，这样当我们要查询一个数的 LIS 长度时，只需要看这个数处于哪个区间中，它的 LIS 长度就是往前（不包括本身）最靠近它的数所对应的 LIS 长度加一。

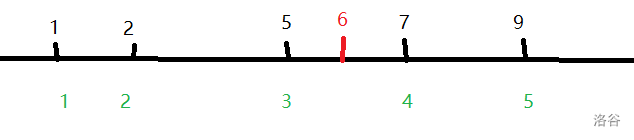
那么可以很快找到 $6$ 的 LIS 长度为 $3 + 1 = 4$。这一个找区间的步骤使用复杂度 $O(\log n)$ 的二分查找。

实现其实并不困难，按照上述的步骤做就行了。

#include <bits/stdc++.h>
using namespace std;

const int M = 1e5 + 5, INF = 1e9;
int n, a[M];
int f[M], g[M], len;
// f[i]   a[i] 为结尾的 LIS 长度
// g[i]   上升子序列长度为 i 时结尾最小值
// len    LIS 长度

int main() {
	int n;
	scanf ("%d", &n);
	for (int i = 1; i <= n; i++) scanf ("%d", &a[i]);
	for (int i = 1; i <= n; i++) {
		int pos = lower_bound(g + 1, g + len + 1, a[i]) - g; //二分查找区间
		f[i] = pos;
		g[pos] = a[i];//查找到之后还要更新最小值
		len = max(len, pos);
	}
	cout << *max_element(f + 1, f + n + 1); //输出最长的 LIS 长度
	return 0;
}

实际上，我们并不需要 f[] 数组，可以直接输出 len。但在本题中需要记录以每个数结尾的 LIS 长度，所以这样写了。

这种做法的时间复杂度是 $O(n \log n)$。依照相同的思路，最长下降子序列长度的求法只需要倒着枚举 i 即可。

本题解法

如我们分析的题意一样，本题只需要记录以 $a_i$ 为最后一个数的最长上升子序列长度和以 $a_i$ 为第一个数的最长下降子序列长度即可，我们用 f1[] 和 f2[] 来记录这两组数，第 $a_i$ 个数的最长合唱队形就是 f1[i] + f2[i] - 1（中间有重合所以减去 $1$）。用总人数减去最大值就是答案了。

#include <bits/stdc++.h>
using namespace std;

const int M = 1e5 + 5, INF = 1e9;
int a[M], f1[M], f2[M], g[M], len, ans = -INF;

int main() {
    int n;
    scanf ("%d", &n);
    for (int i = 1; i <= n; i++) scanf ("%d", &a[i]);
    len = 0;
    for (int i = 1; i <= n; i++) {
        int pos = lower_bound(g + 1, g + len + 1, a[i]) - g;
        f1[i] = pos;
        g[pos] = a[i]; 
        len = max(len, pos);
    }
    len = 0;
    memset(g, 0, sizeof g);
    for (int i = n; i >= 1; i--) {
        int pos = lower_bound(g + 1, g + len + 1, a[i]) - g;
        f2[i] = pos;
        g[pos] = a[i];
        len = max(len, pos);
    }
    for (int i = 1; i <= n; i++) ans = max(ans, f1[i] + f2[i] - 1);
    cout << n - ans;
    return 0;
}

dp 的想法

还是介绍一下比较有用的 dp 吧。

考虑设 $f_i$ 表示考虑完前 $i$ 个数，强制以 $i$ 结尾的最长上升子序列。枚举上一个选的位置 $j$，需要满足 $a_j < a_i$，我们在 $j$ 处已经求得以 $j$ 结尾的最长的长度是 $f_j$，于是 $f_i \gets f_j+1$ 即可。可以写成式子：

$$f_i=\max_{j=1}^{i-1} f_j+1 \ \ \texttt{s.t.} a_j<a_i$$。 ### 优化至 $O(n \log n)$ 考虑维护一个值域数据结构（你可以认为是一个树状数组）并做扫描线（你可以认为是从 $1$ 到 $n$ 遍历），扫描到 $i$ 时，在值域 $a_i$ 处用 $f_i$ 更新最大这个值域的最大值，这样，我们可以通过查询值域 $[0,a_i-1]$ 的最大值来获得满足 $a_j < a_i$ 的最大 $f_j$。可以用树状数组或者线段树实现。时间复杂度 $O(n\log n)$。$$