自动搬运

查看原文

来自洛谷，原作者为

	OIer_Eternity 陪你看日落的人，比日落本身更温柔.

搬运于2025-08-24 23:02:15，当前版本为作者最后更新于2024-08-21 21:44:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Description

定义一个序列为「安全的」当且仅当其所有前缀和均大于 $0$。

先给定一个长度为 $n$ 的序列 $A_0$，将进行如下操作 $k$ 次：

• 第 $i$ 次操作将会由 $A_{i-1}$ 得到 $A_i$。
• 重复如下操作 $n$ 次：
  • 若 $A_{i-1}$ 是「安全的」就将其接到 $A_i$ 末尾。
  • 将 $A_{i-1}$ 循环左移 $1$ 位。

求 $\dfrac{|A_{k+1}|}{|A_k|}$。

Solution

首先考虑 $k=0$ 的情况。

我们只需统计满足以第 $t$ 位开头的序列是「安全的」的 $t$ 的个数（我们称满足条件的 $t$ 所代表的位置是「被标记的」）。

则我们需要用到前缀和的极小值，线段树或树状数组维护即可。

接着拓展到 $k>0$ 的情况，我们令 $f(p)$ 表示 $A_p$ 中「被标记的」位置的个数，考虑如何计算 $f(p)$。

首先，在前一个序列 $A_p$ 中「被标记的」位置在当前序列 $A_{p+1}$ 一定是「被标记的」，并且 $A_{p+1}$ 的长度是 $A_p$ 的 $f(p)$ 倍。

那么有 $\forall p\in[1,k],f(p)\ge f^2(p-1)$。

接着考虑是否会出现新的「被标记的」位置。

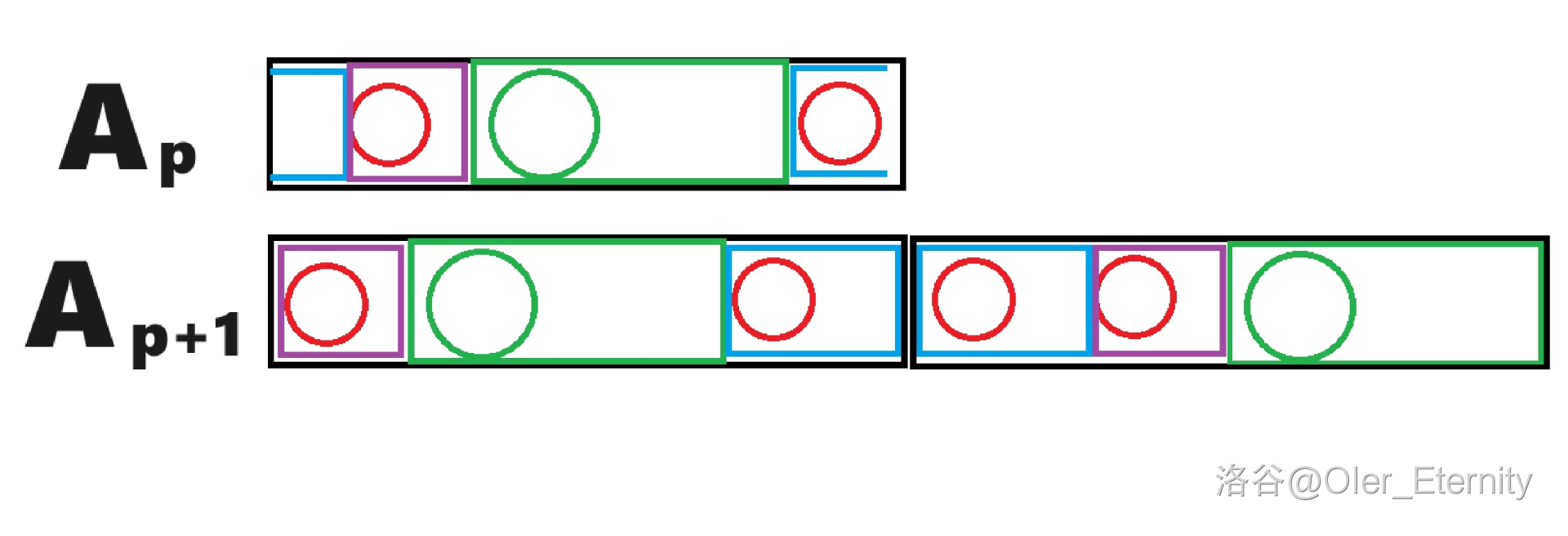
如图，若设红色的圈表示在 $A_p$ 中「被标记的」的位置，绿色的圈表示 $A_{p+1}$ 中新出现的「被标记的」的位置，则各个颜色所代表的矩形对应相同，且各矩形的前缀和一定大于 $0$。

那么在 $A_p$ 中，以绿色的圈开头也是一个「安全的」序列，矛盾。

因此 $f(p)=f^2(p-1)$，依次计算 $f(p),p\in[1,k]$，答案即为 $f(p)$。

AC Code

#include <bits/stdc++.h>
using namespace std;
const int p=998244353;
int n,k;
long long a[2000005];
struct Node{
    int l,r;
    long long Min;
}tree[8000005];
void build(int p,int l,int r){
    tree[p].l=l,tree[p].r=r;
    if (l==r){
        tree[p].Min=a[l];
        return;
    }
    int Mid=(l+r)>>1;
    build(p<<1,l,Mid);
    build(p<<1|1,Mid+1,r);
    tree[p].Min=min(tree[p<<1].Min,tree[p<<1|1].Min);
}
long long query(int p,int l,int r){
    if (l<=tree[p].l&&tree[p].r<=r) return tree[p].Min;
    int Mid=(tree[p].l+tree[p].r)>>1;
    long long res=1e18;
    if (l<=Mid) res=query(p<<1,l,r);
    if (r>Mid) res=min(res,query(p<<1|1,l,r));
    return res;
}
int qpow(int a,int b){
    int res=1;
    for (;b;b>>=1,a=1ll*a*a%p) if (b&1) res=1ll*res*a%p;
    return res;
}
int main(){
    scanf("%d%d",&n,&k);
    for (int i=1;i<=n;i++) scanf("%lld",&a[i]),a[i+n]=a[i];
    for (int i=1;i<=2*n;i++) a[i]+=a[i-1];
    build(1,1,2*n);
    int ans=0;
    for (int i=1;i<=n;i++) if (query(1,i,i+n-1)>a[i-1]) ans++;
    for (int i=1;i<=k;i++) ans=1ll*ans*ans%p;
    printf("%d\n",ans);
    return 0;
}