自动搬运

查看原文

来自洛谷，原作者为

	Otomachi_Una_ We will never forget those days, thanks for everything.

搬运于2025-08-24 23:02:04，当前版本为作者最后更新于2024-10-19 15:38:26，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

【鸣谢】

感谢树姐姐给予思路的启发。

【题目简述】

在 $n\times m$ 的方格中找到 $(x_1,y_1)$ 到 $(x_2,y_2)$ 的最长路。

对于部分测试点只需要输出长度。

$1\leq n,m\leq 5000$，$1\leq \sum nm\leq 1\times 10^5$。

【解题思路】

先来解决 $type=1$ 的问题。下面提到答案指最长路的长度。

我们不妨假设 $n\leq m$，$x_1\leq x_2$，$y_1\leq y_2$。

直觉告诉我们在大多数情况下，答案直接黑白染色分析奇偶就出来了。

我们打个表，把不满足黑白染色规律的 $(n,m,x_1,y_1,x_2,y_2)$ 找出来。

我们发现这些不符合条件的都满足 $n\leq 3$。我们来分类讨论一下：

• 当 $n=1$，答案显然是 $y_2-y_1$。
• 当 $n=2$，如果 $x_1=1,x_2=2$ 且 $y_2-y_1\leq 1$。那么此时 $(x_1,y_1),(x_2,y_2)$ 把整个格子分割成两部分，取最大的一边即可。
• 当 $n=3$，这时情况比较多。但是仔细观察都能发现此时不符合的 $m$ 必然为偶数。这里需要读者自己打表找规律。或者见下面的代码。下图呈现了几种可能的不合法情况。

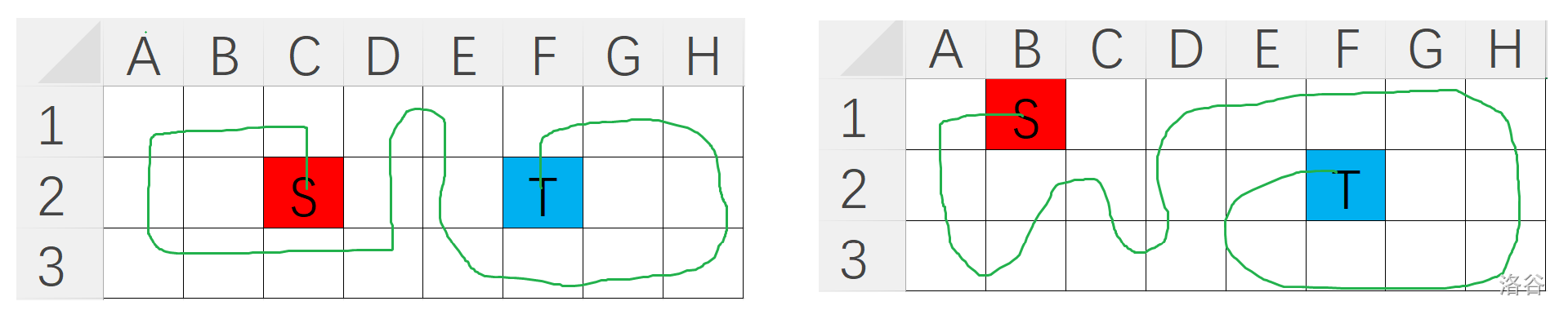
在完成对 $type=1$ 的问题之后，我们可以进行递归了。下图是一种容易想到的递归方式：

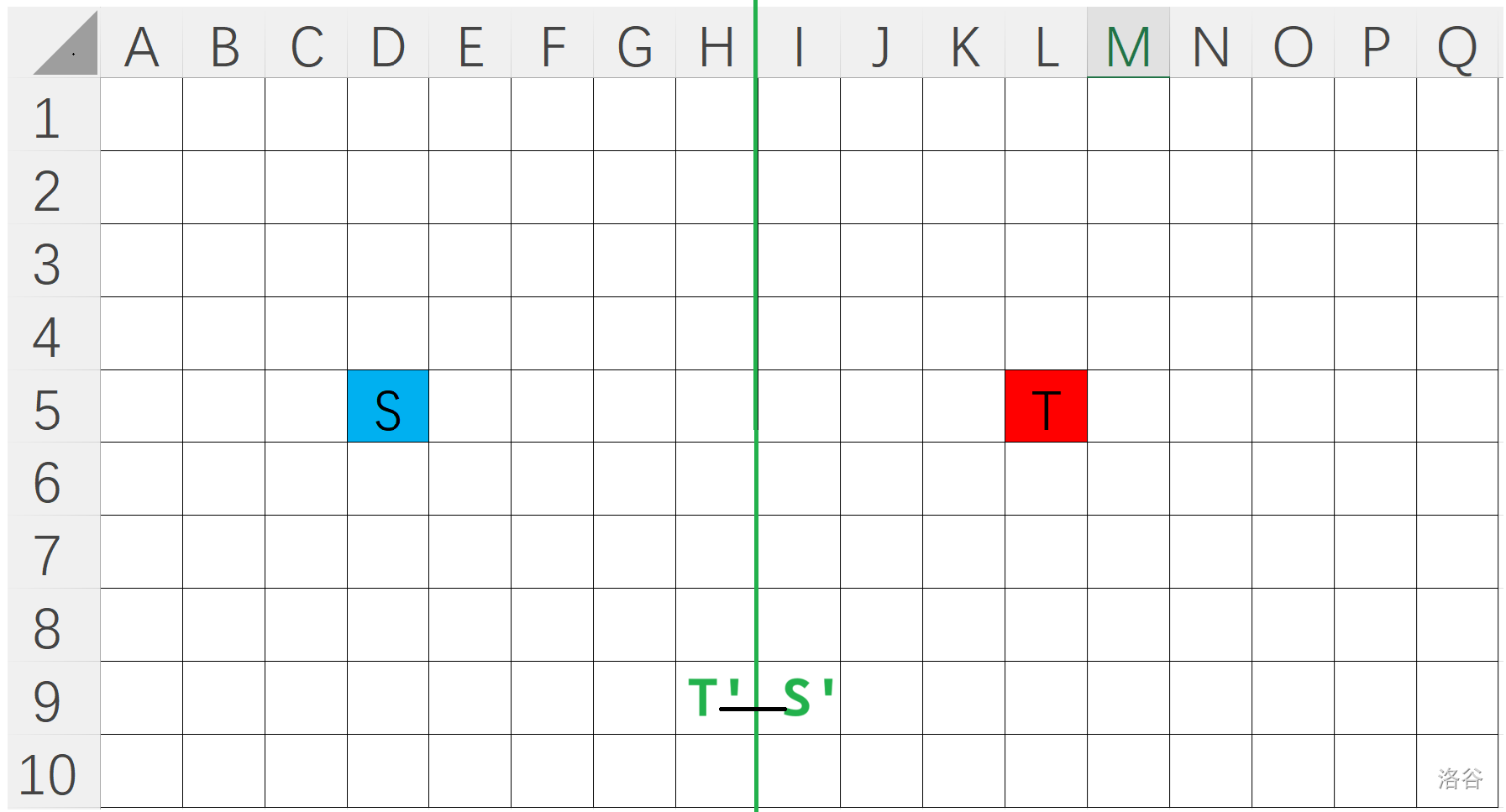
我们以绿色线为分割线，先把左边 $S\to T'$ 再到 $S'\to T$。

如果我们两边最大步数的和恰好为我原图的最大步数，我们便完成可递归。

上面是对 $y$ 的分割，对 $x$ 的分割同理。

此时仍然有部分情况没有被成功分治，我们打表，来一一攻破。

首先是 $n=3$ 的情况。通过打表，发现这类情况总有 $y_2-y_1\leq 1$。分类讨论一下就行了。

剩下的情况总满足 $x_1=x_2$ 或者 $y_1=y_2$。不妨让 $y_1=y_2$。我们人类智慧地再来进行分治：

下面列出了 $4$ 种可能分治的情况，实际上对称一下一共有 $8$ 种。

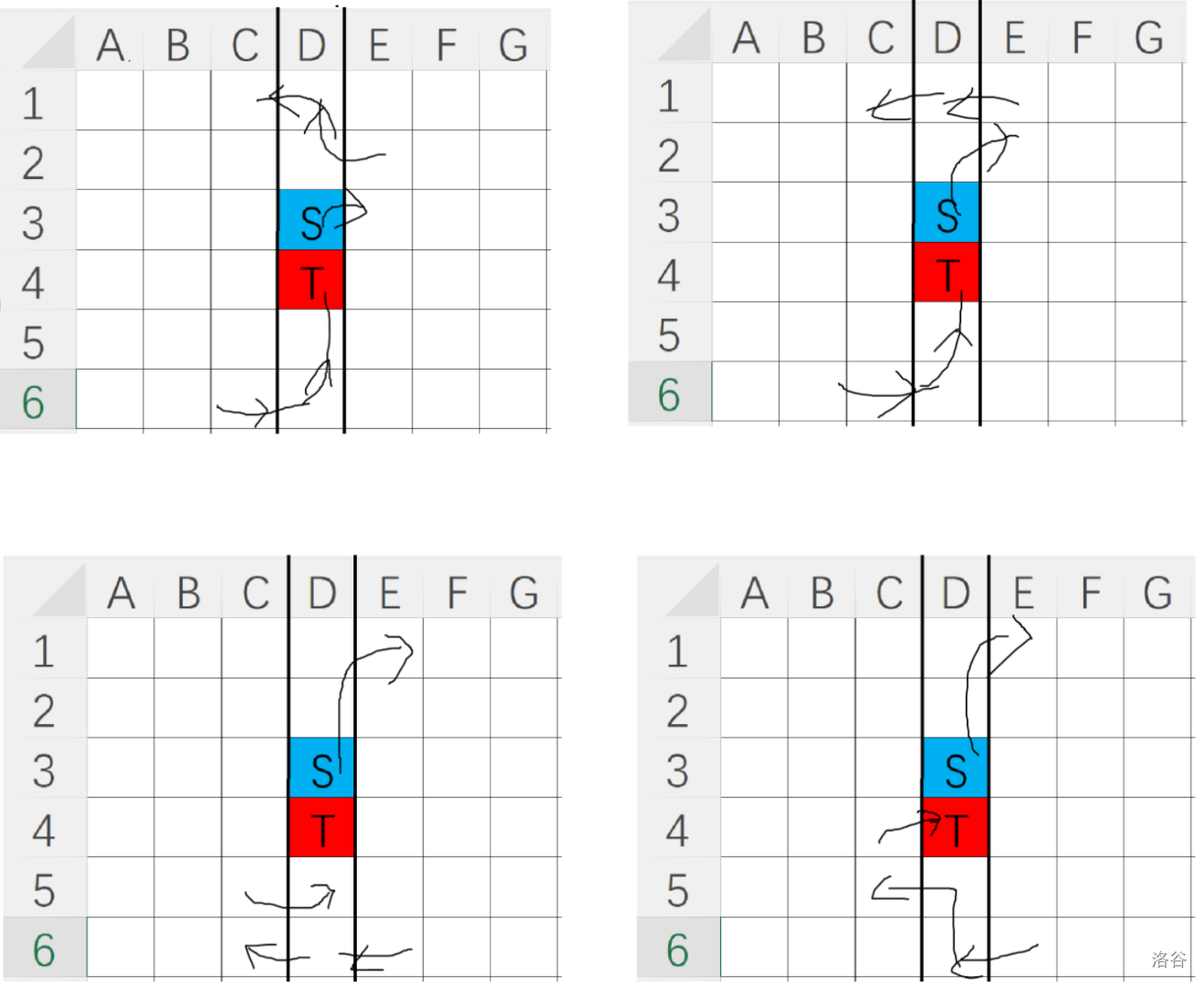
讨论完这几种情况你就发现没有分治不了的东西了。完结撒花~

【参考代码】

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define MP make_pair
mt19937 rnd(time(0));
const int MAXN=5005;
int tid,T;
bool ri[MAXN][MAXN],dw[MAXN][MAXN];
bool vis[MAXN][MAXN];
map<array<int,6>,string> mp;
int max_len(int n,int m,int x1,int y1,int x2,int y2){
	if(x1==x2&&y1==y2) return 1;
	if(n>m) return max_len(m,n,y1,x1,y2,x2);
	if(x1>x2) return max_len(n,m,n+1-x1,y1,n+1-x2,y2);
	if(y1>y2) return max_len(n,m,x1,m+1-y1,x2,m+1-y2);
	if(n==1) return y2-y1+1;
	if(n==2&&x2-x1==1&&y2-y1<=1) return max(y1+y2,2*m+2-y1-y2);
	if(n*m&1) return n*m-((x1+y1)&1)-((x2+y2)&1);
	if(n==3&&((x1+x2+y1+y2)&1)&&((y2-y1>=2&&((x1+y1)&1))||(x1==2&&x2==2&&(y1&1)))) return n*m-2;
	return n*m-(~(x1+x2+y1+y2)&1); 
}
string replace(string s,char L,char R,char U,char D){
	for(int i=0;i<s.length();i++){
		if(s[i]=='L') s[i]=L;
		else if(s[i]=='R') s[i]=R;
		else if(s[i]=='U') s[i]=U;
		else if(s[i]=='D') s[i]=D;
	}
	return s;
}
string rev(string s){
	reverse(s.begin(),s.end());
	return replace(s,'R','L','D','U');
}
string solve(int n,int m,int x1,int y1,int x2,int y2){
	if(x1==x2&&y1==y2) return (string){};
	if(mp.count({n,m,x1,y1,x2,y2})) return mp[{n,m,x1,y1,x2,y2}];
	if(n>m) return replace(solve(m,n,y1,x1,y2,x2),'U','D','L','R');
	if(x1>x2) return replace(solve(n,m,n+1-x1,y1,n+1-x2,y2),'L','R','D','U');
	if(y1>y2) return replace(solve(n,m,x1,m+1-y1,x2,m+1-y2),'R','L','U','D');
	if(n==1) return string(y2-y1,'R');
	int C=max_len(n,m,x1,y1,x2,y2);
	for(int x=1;x<=n;x++) if(x1<=x&&x<x2) for(int y=1;y<=m;y++){
		if(C==max_len(x,m,x1,y1,x,y)+max_len(n-x,m,1,y,x2-x,y2)){
			return mp[{n,m,x1,y1,x2,y2}]=solve(x,m,x1,y1,x,y)+"D"+solve(n-x,m,1,y,x2-x,y2);
		}
	}
	for(int y=1;y<=m;y++) if(y1<=y&&y<y2) for(int x=1;x<=n;x++){
		if(C==max_len(n,y,x1,y1,x,y)+max_len(n,m-y,x,1,x2,y2-y)){
			return mp[{n,m,x1,y1,x2,y2}]=solve(n,y,x1,y1,x,y)+"R"+solve(n,m-y,x,1,x2,y2-y);
		}
	}
	if(n==3&&y1==y2){
		int x3=6-x1-x2;
		if(3+max_len(3,y1-1,x1,y1-1,x3,y1-1)+max_len(3,m-y1,x3,1,x2,1)==C){
			return mp[{n,m,x1,y1,x2,y2}]="L"+solve(3,y1-1,x1,y1-1,x3,y1-1)+"RR"+
			solve(3,m-y1,x3,1,x2,1)+"L";
		}
		if(3+max_len(3,m-y1,x1,1,x3,1)+max_len(3,y1-1,x3,y1-1,x2,y1-1)==C){
			return mp[{n,m,x1,y1,x2,y2}]="R"+solve(3,m-y1,x1,1,x3,1)+"LL"+
			solve(3,y1-1,x3,y1-1,x2,y1-1)+"R";
		}
	}else if(n==3&&y2-y1==1){
		assert(x1==1&&x2==3);
		if(6+max_len(3,m-y2,1,1,2,1)+max_len(3,y1-1,2,y1-1,3,y1-1)==C)
			return mp[{n,m,x1,y1,x2,y2}]="RR"+solve(3,m-y2,1,1,2,1)+"LLL"+
			solve(3,y1-1,2,y1-1,3,y1-1)+"RR";
	}
	bool flag=(x1==x2);string s;
	if(flag) swap(n,m),swap(x1,y1),swap(x2,y2);
	for(int o:{0,1}){
	for(int i=x2+1;i<=n;i++){
		if(n+max_len(n,m-y1,1,1,i,1)+max_len(n,y1-1,n,y1-1,i-1,y1-1)==C){
			s=string(x1-1,'U')+"R"+solve(n,m-y1,1,1,i,1)+"L"+string(n-i,'D')+"L"+
			solve(n,y1-1,n,y1-1,i-1,y1-1)+"R"+string(i-1-x2,'U');
			if(o) s=replace(s,'R','L','U','D');
			if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
			return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
		}else if(n+max_len(n,m-y1,1,1,n,1)+max_len(n,y1-1,i,y1-1,i-1,y1-1)==C){
			s=string(x1-1,'U')+"R"+solve(n,m-y1,1,1,n,1)+"L"+string(n-i,'U')+"L"+
			solve(n,y1-1,i,y1-1,i-1,y1-1)+"R"+string(i-1-x2,'U');
			if(o) s=replace(s,'R','L','U','D');
			if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
			return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
		}
	}
	for(int i=1;i<x1;i++){
		if(n+max_len(n,m-y1,i+1,1,i,1)+max_len(n,y1-1,1,y1-1,n,y1-1)==C){
			s=string(x1-i-1,'U')+"R"+solve(n,m-y1,i+1,1,i,1)+"L"+string(i-1,'U')+"L"+
			solve(n,y1-1,1,y1-1,n,y1-1)+"R"+string(n-x2,'U');
			if(o) s=replace(s,'R','L','U','D');
			if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
			return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
		}else if(n+max_len(n,m-y1,i+1,1,1,1)+max_len(n,y1-1,i,y1-1,n,y1-1)==C){
			s=string(x1-i-1,'U')+"R"+solve(n,m-y1,i+1,1,1,1)+"L"+string(i-1,'D')+
			"L"+solve(n,y1-1,i,y1-1,n,y1-1)+"R"+string(n-x2,'U');
			if(o) s=replace(s,'R','L','U','D');
			if(!flag) return mp[{n,m,x1,y1,x2,y2}]=s;
			return mp[{n,m,x1,y1,x2,y2}]=replace(s,'U','D','L','R');
		}
	}
	y1=y2=m+1-y1;
	}
	assert(0);
}
int main(){
	ios::sync_with_stdio(false);
	// freopen("Otomachi_Una.in","r",stdin);
	// freopen("Otomachi_Una.out","w",stdout);
	cin>>tid>>T;
	while(T--){
		int n,m,x1,y1,x2,y2;
		cin>>n>>m>>x1>>y1>>x2>>y2;
		if(tid) cout<<max_len(n,m,x1,y1,x2,y2)<<'\n';
		else{
			string s=solve(n,m,x1,y1,x2,y2);
			for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) vis[i][j]=ri[i][j]=dw[i][j]=0;
			int x=x1,y=y1;
			for(char c:s){
				vis[x][y]=true;
				if(c=='L'){
					ri[x][--y]=true;
				}else if(c=='R'){
					ri[x][y++]=true;
				}else if(c=='U'){
					dw[--x][y]=true;
				}else{
					dw[x++][y]=true;
				}
			}
			for(int i=1;i<=n;i++){
				for(int j=1;j<=m;j++){
					cout<<"o*"[(i==x1&&j==y1)||(i==x2&&j==y2)];
					if(j<m) for(int o:{0,1}) cout<<" -"[ri[i][j]];
				}
				cout<<'\n';
				if(i<n){
					for(int j=1;j<=m;j++){
						cout<<" |"[dw[i][j]];
						if(j<m) cout<<"  ";
					}
					cout<<'\n';
				}
			}
		}
	}
	cerr<<"Running time: "<<1.*clock()/CLOCKS_PER_SEC<<'\n';
	return 0;
}