自动搬运

查看原文

来自洛谷，原作者为

	a1a2a3a4a5 蒟蒻可骂，私信互关，互关者备故事来

搬运于2025-08-24 23:01:34，当前版本为作者最后更新于2025-07-30 16:58:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意：

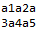
求 $x$，使得以 $x$ 为参数的随机排序可以把排列 $1,2,3,4,…,n$ 排成 $a$ 序列，具体信息看题面的代码。

思路

省选模拟赛这题放在了 T2，可以推断出不是诈骗题，所以我们不得不从代码中推出一些性质：

一

for (int i = 1; i <= n; i++)
{
    a[i] = i;
    swap(a[i], a[rand() % i + 1]);
}

发现这是前缀交换，所以最后一个数只会被交换一次。设 $n$ 在 $a_p$，那么 $\operatorname{rand}\bmod n+1=p$，然后再 swap(a[p],a[n])，那么相当于抛去了 $n$ 的影响，现在 $n-1$ 是最后一个数……
我们推出了：
$\operatorname{rand}\bmod n+1=p$
$\operatorname{rand}\bmod(n-1)+1=p'$
$\operatorname{rand}\bmod(n-2)+1=p''$
……

二

uint64_t rand()
{
    x ^= x << 13;
    x ^= x >> 7;
    x ^= x << 17;
    return x;
}

我们的 $x$ 与 $\operatorname{rand}$ 有关，我们考虑用 $x$ 表示 $\operatorname{rand}$。
由于 $x'=\operatorname{rand}(n)$ 所以下面我都用 $x'$ 来表示 $\operatorname{rand}(n)$。

手玩一下左右移异或的性质，为了方便，我们手玩下面这份代码：

uint64_t rand()
{
    x ^= x << 1;
    x ^= x >> 2;
    return x;
}

假设 $x_{(2)}=101$ （二进制表示）。
$x$ 左移 $1$ 位为 $1010$
$1010$ 右移 $2$ 位为 $10$
结果为 $(101\operatorname{xor} 1010)\operatorname{xor} 10=1101$，每一位的来源我们可以记录下来，此例：
$101=x_1x_2x_3$
$1010=x_1x_2x_30$
$10=x_1x_2$
$1101=(x_1)(x_1\operatorname{xor}x_2)(x_2\operatorname{xor}x_3\operatorname{xor}x_1)(x_3\operatorname{xor}x_2)$
所以关于 $x$ 的方程组大概是这样的：
$x'=(x_1)(x_1\operatorname{xor}x_2)(x_2\operatorname{xor}x_3\operatorname{xor}x_1)(x_3\operatorname{xor}x_2)$

综上，我们可以把 $x'$ 的每一位用 $x$ 来表示，然后 $x''$ 也用 $x'$ 的 $x$ 表示来表示……最终所有式子都化成了初始的 $x$，这样我们就处理了 $x$ 变化带来的影响并把所有 $\operatorname{rand}$ 值都用 $x$ 表示出来了（$\operatorname{rand}$ 就是上文的 $x'、x''$）。

三

移项整理上面两个性质，这里写的 $x^2$ 的意思是 $x''$，而并非次方：
$x^n\equiv p-1 \pmod n$
$x^{n-1}\equiv p'-1 \pmod{(n-1)}$
$x^{n-2}\equiv p''-1 \pmod{(n-2)}$
……
我们显然是想解方程似得把 $x$ 解出来，我们性质二的 $x'$ 是依赖二进制位的，所以我们不得不把上面这个式子在二进制上考虑。$x$ 拆成二进制，猜出模数拆成二进制数肯定不劣，我们考虑二进制如何取模？
先分类思考一下，如果模数为 $2^x$，那么取模相当于保留了后 $x$ 位。在上面式子相当于可以直接求出 $x'$ 后几个二进制位，然后我们可以得到只有 $x_i$ 未知的帅方程。帅方程可以用线性基解，所以我们可以找出 $2^x$ 模数找出他们的帅方程。

但是这样做感觉方程好少啊！

此时宇宙射线横着走过来说：“ 不是，我不是二的整次幂，我直接把多的位数不要了不得了？ 然后我再跟你说：
对于 $p=2^xq$，$(n\bmod p)\equiv n\pmod{2^x}$。
证明：
$n=kp+(n\bmod p)=kq2^x+(n\bmod p)$，则 $(n\bmod p)\equiv n\pmod{2^x}$。”

真是说的道理，我们模 $p$ 的式子再模一个 $2^x$ 肯定还成立，我们直接取后 $x$ 位并对右边的常数模 $2^x$ 再拿来写方程就好了。
关于为什么取 $lowbit$，因为你除以这玩意就是奇数了，所以这玩意就是 $2^x$。

终末之章

显然我们后来推的都是必要条件，因为充要条件没法推，难道真的无法做到吗？可是！你别忘了！我们 OI 从来都是把必要当充分用的啊！！！

我们现在相当于有 $x$ 的一些位数没有解出来，祈祷其少——指数级枚举，到最后还是选择了暴力吗？对不起 T2 大人，我没让你用尽全力……

跑得...
飞快吗？