自动搬运

查看原文

来自洛谷，原作者为

	Federico2903 AFOed | 洛谷保存站站长之一 | QQ 1593377822

搬运于2025-08-24 23:01:28，当前版本为作者最后更新于2024-06-20 20:25:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

0. 前言

应该是一道比较简单的双极定向题，只要你舍得花时间去分类讨论应该就能做。

前置芝士：点双连通分量，圆方树。

1. 思路

原题要求的即是加入一条边后原图存在双极定向的概率，考虑我们连接原图两个点后发生了什么。连接两个点相当于把这两点之间的方点缩成一个方点。

如下图所示：

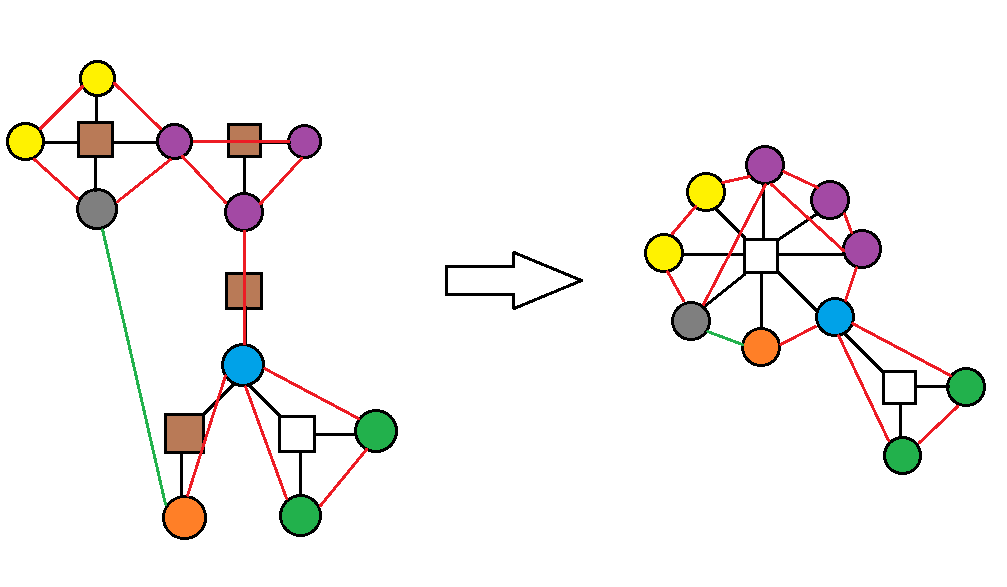
考虑双极定向存在的条件是原图连接 $S \to T$ 后点双连通，即原图圆方树的方点形成一条链且 $S, T$ 是其一条直径，我们称原图圆方树的方点的虚树为 $G$，若 $G$ 中存在一个大于 $2$ 个三度点或大于一个四度点一定 $P = 0$，故有如下的情况：

$1. G$ 是一条链

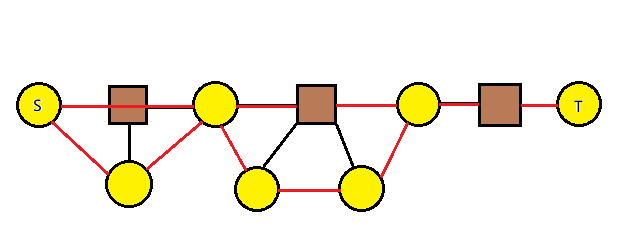
显然在这种情况中，连接的边除了自环都满足要求。

2. $G$ 仅存在一个三度点，三度点是方点，其余点度数 $\le 2$

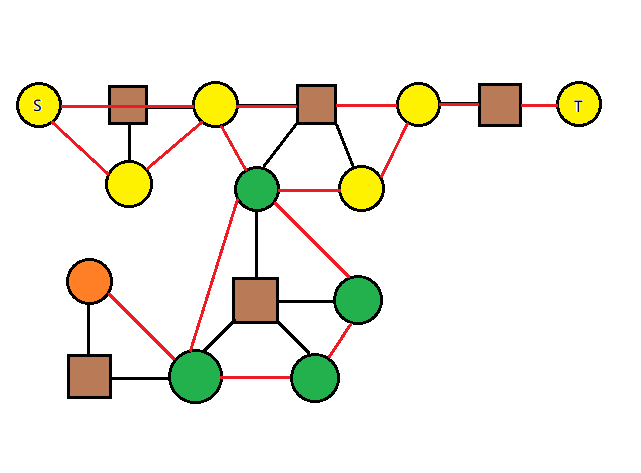
可以选择外挂的这条链的链底方点的任意一个一度圆点（橙色）连接主链的任意圆点（黄色）。

3. $G$ 仅存在一个三度点，三度点是圆点，其余点度数 $\le 2$

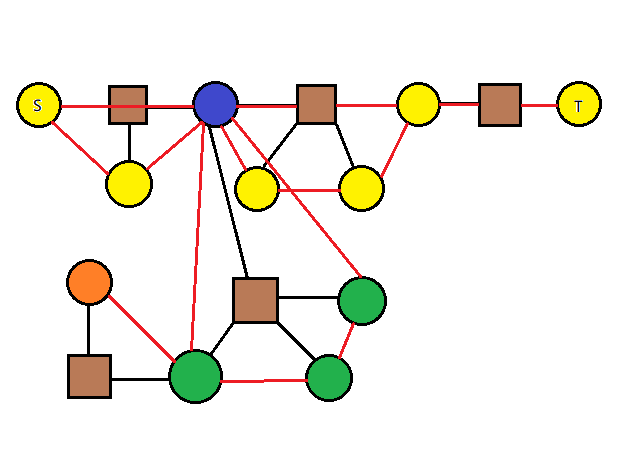
可以选择外挂的这条链的链底方点的任意一个一度圆点（橙色）连接主链的任意圆点（黄色），但不能连接三度点（蓝色）。

4. $G$ 恰存在两个三度点，其余点度数 $\le 2$

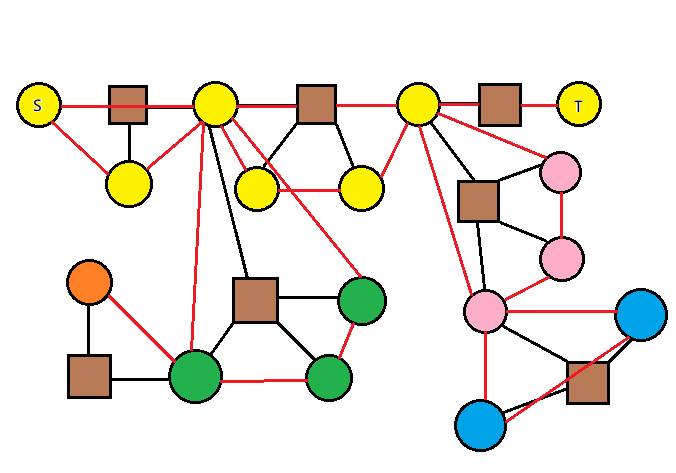
可以选择两条外挂链的链底方点的任意一度圆点连接（橙色，蓝色）。

5. $G$ 恰存在一个四度点，四度点是圆点，其余点度数 $\le 2$

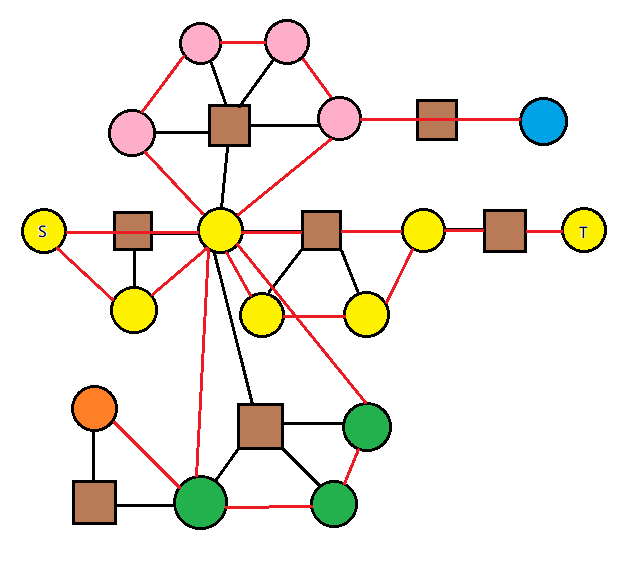
显然无解。

6. $G$ 恰存在一个四度点，四度点是方点，其余点度数 $\le 2$

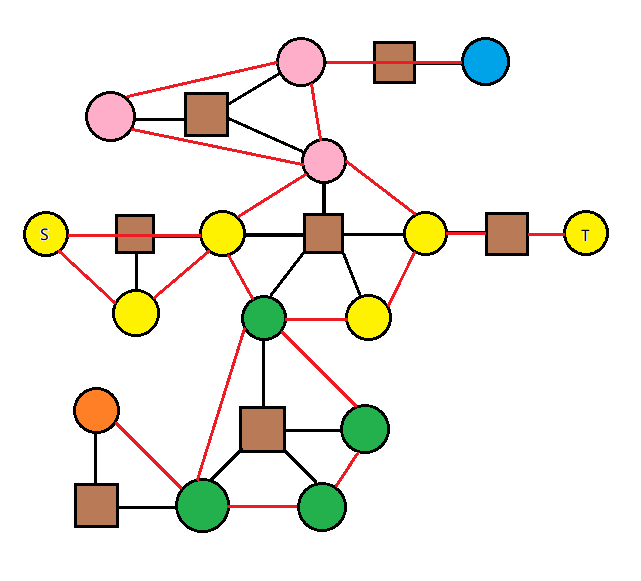
构造方式同 $4$。

那么算出方案数除以总的方案数就可以得到概率了。

然后随便连边跑双极定向即可。

对于无解的情况，连接 $S \to T$ 后重新构建圆方树，把除 $S, T$ 所在点双以外的所有点删掉，一定是最优的。

代码：7.47KB。