15011418730 LV 7 @ 2025-8-24 23:01:05

自动搬运

来自洛谷，原作者为

	yzljy 福瑞难道不可爱吗qwq

搬运于2025-08-24 23:01:05，当前版本为作者最后更新于2025-03-14 16:48:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

UPD：增加和修改了一些内容，辛苦管理员了。

题目链接

前言

随机跳题跳到的。我并不会题解区另外两篇大佬的做法，我用了一种相对更加复杂的拆式子。似乎这种拆式子的方法更为通用一些？比如疯狂动物城也可以用类似的拆法实现。
题意题面已经很简洁了，注意一下是先减少价值，再产生费用就行了。
到我的博客也许能有更优的阅读体验：这里

思路

首先我们令 $dis(x,y)$ 表示从 $x$ 到 $y$ 经过的边的 $T_{i}$ 和。 $D_{i}$ 在边上不好做，我们使用边权转点权，将一条边的 $D_{i}$ 的值，放到这条边相连的两个点中，深度更深的那个上面。（这个是很常见的边权转点权的方法）

记 $S(x,y)$ 表示从 $x$ 到 $y$ 的点集。
根据题意，我们可以写出这样的式子：

$$\begin{aligned} ans=&\left(\sum_{i\in S(x,\operatorname{LCA}(x,y)),i\not=\operatorname{LCA}(x,y)}D_{i}(dis(fa_{i},y)+G)\right)+\\ &\left(\sum_{i\in S(\operatorname{LCA}(x,y),y),i\not=\operatorname{LCA}(x,y)}D_{i}(dis(i,y)+G)\right)\\ \end{aligned} $$

没有看懂式子的话，可以画一下图，模拟一下。

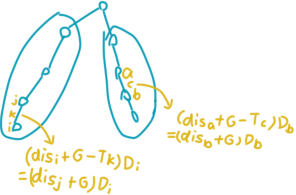
看着十分吓人，我们可以先将 $G$ 提出来，再将 $dis(x,y)$ 展开成 $dep_{x}+dep_{y}-2dep_{\operatorname{LCA}(x,y)}$ 。
（ $dep_i$ 也就是从 $1$ 号点到 $i$ 号点的边的 $T$ 和）

对于 $i\in S(x,\operatorname{LCA}(x,y))$ ，都有 $\operatorname{LCA}(i,y)=\operatorname{LCA}(x,y)$ 。
对于 $i\in S(\operatorname{LCA}(x,y),y)$ 都有 $\operatorname{LCA}(i,y)=i$ 。

那么我们便可以写成这样的式子：

$$\begin{aligned} ans=&\left(G\sum_{i\in S(x,y),i\not=\operatorname{LCA}(x,y)}D_{i}\right)+\\ &\left(\sum_{i\in S(x,\operatorname{LCA}(x,y)),i\not=\operatorname{LCA}(x,y)}D_{i}(dep_{fa_{i}}+dep_{y}-2dep_{\operatorname{LCA}(x,y)})\right)+\\ &\left(\sum_{i\in S(\operatorname{LCA}(x,y),y),i\not=\operatorname{LCA}(x,y)}D_{i}(dep_{y}-dep_{i})\right) \end{aligned} $$

展开化简一下，得到：

$$\begin{aligned} ans=&\left(\left(G+dep_{y}\right)\sum_{i\in S(x,y),i\not=LCA(x,y)}D_{i}\right)+\\ &\left(\sum_{i\in S(x,LCA(x,y)),i\not=LCA(x,y)}D_{i}dep_{fa_{i}}\right)-\\ &\left(2dep_{LCA(x,y)}\sum_{i\in S(x,LCA(x,y)),i\not=LCA(x,y)}D_{i}\right)-\\ &\left(\sum_{i\in S(LCA(x,y),y),i\not=LCA(x,y)}D_{i}dep_{i}\right)\\ \end{aligned} $$

我们发现这些都是可以使用线段树来维护的。
我们需要维护的也就是：

区间 $D_{i}$ 和
区间 $dep_{i}$ 和
区间 $D_{i}dep_{i}$ 和
区间 $D_{i}dep_{fa_{i}}$ 和

第一个是不变的，可以用一个前缀和简单实现（写线段树也可以）。
第二个我们发现和 $T_{i}$ 有关，而修改一条边 $x$ 到 $y$ （设 $y$ 点更深）的边权为 $t$ 后，会对 $y$ 及其子树的 $dep_{i}$ 一起增加 $t-T_{i}$ （ $T_{i}$ 为改之前的边权）。对原树进行树剖重新标号后，这是一个区间加的操作。
第三个可以看作维护 $kx,x=\sum dep_{i}$ ，也就是增加倍数的操作。
第四个和第三个一样，因为我们每次修改的时候，会对一整棵子树进行修改，所以 $dep_{fa_{i}}$ 没变的只有这棵子树的根（也就是第二点中提到的 $y$ ），特殊处理一下就行了。

那么到这里就结束了，维护起来还是有一点麻烦的。

代码

参考一下就好啦。

// Problem: P10773 [NOISG 2021 Qualification] Truck
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P10773
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+10;
const int mod=1e9+7;
const int inf_int=0x7f7f7f7f;
const long long inf_long=0x7f7f7f7f7f7f7f7f;
const double eps=1e-9;
char Buf[1<<23],*P1=Buf,*P2=Buf;
#define getchar() (P1==P2&&(P2=(P1=Buf)+fread(Buf,1,1<<23,stdin),P1==P2)?EOF:*P1++)
template<typename type>
inline void read(type &x){
	x=0;
	bool f=false;
	char ch=getchar();
	while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
	if(f) x=-x;
}
template<typename type,typename... args>
inline void read(type &x,args&... y){
	read(x),read(y...);
}

int n,g,k,q,cnt,head[MAXN],Dep[MAXN],val[MAXN],hson[MAXN]；
int dfsnum[MAXN],dfsnod[MAXN],top[MAXN],fa[MAXN],dep[MAXN],siz[MAXN];
map<pair<int,int>,int> mp;
struct node{
	int to,next,val1,val2;
}edge[MAXN<<1];
struct node2{
	int l,r,val1,val2,val3,val4,lazy;
}tree[MAXN<<2];

void build(int u,int v,int d,int t){
	edge[++k].to=v;
	edge[k].next=head[u];
	edge[k].val1=t;
	edge[k].val2=d;
	head[u]=k;
}

void dfs(int u,int f){
	siz[u]=1;
	int maxsiz=0;
	for(int i=head[u];i;i=edge[i].next){
		int v=edge[i].to;
		if(v==f) continue;
		fa[v]=u;
		dep[v]=(dep[u]+edge[i].val1)%mod;
		Dep[v]=Dep[u]+1;
        //因为T_i可能为0，所以额外记录一下深度。
		val[v]=edge[i].val2;
		dfs(v,u);
		siz[u]+=siz[v];
		if(maxsiz<siz[v]){
			maxsiz=siz[v];
			hson[u]=v;
		}
	}
}

void dfs2(int u,int f){
	top[u]=f;
	dfsnum[u]=++cnt;
	dfsnod[cnt]=u;
	if(hson[u]==0) return;
	dfs2(hson[u],f);
	for(int i=head[u];i;i=edge[i].next){
		int v=edge[i].to;
		if(v==fa[u]||v==hson[u]) continue;
		dfs2(v,v);
	}
}

void pushup(int id){
	tree[id].val1=(tree[id*2].val1+tree[id*2+1].val1)%mod;
	tree[id].val2=(tree[id*2].val2+tree[id*2+1].val2)%mod;
	tree[id].val3=(tree[id*2].val3+tree[id*2+1].val3)%mod;
	tree[id].val4=(tree[id*2].val4+tree[id*2+1].val4)%mod;
}

void pushdown(int id){
	if(tree[id].lazy==0) return;
	tree[id*2].val2+=tree[id].lazy;
	tree[id*2].val3+=tree[id*2].val1*(tree[id].lazy%mod)%mod;
	tree[id*2].val4+=tree[id*2].val1*(tree[id].lazy%mod)%mod;
	tree[id*2].lazy+=tree[id].lazy;
	tree[id*2].val2%=mod;
	tree[id*2].val3%=mod;
	tree[id*2].val4%=mod;
	tree[id*2+1].val2+=tree[id].lazy;
	tree[id*2+1].val3+=tree[id*2+1].val1*(tree[id].lazy%mod)%mod;
	tree[id*2+1].val4+=tree[id*2+1].val1*(tree[id].lazy%mod)%mod;
	tree[id*2+1].lazy+=tree[id].lazy;
	tree[id*2+1].val2%=mod;
	tree[id*2+1].val3%=mod;
	tree[id*2+1].val4%=mod;
	tree[id].lazy=0;
}

void build_tree(int id,int l,int r){
	tree[id].l=l;
	tree[id].r=r;
	tree[id].lazy=0;
	tree[id].val1=tree[id].val2=tree[id].val3=tree[id].val4=0;
	if(l==r){
		tree[id].val1=val[dfsnod[l]];
		tree[id].val2=dep[dfsnod[l]];
		tree[id].val3=tree[id].val1*dep[dfsnod[l]]%mod;
		tree[id].val4=tree[id].val1*dep[fa[dfsnod[l]]]%mod;
		return;
	}
	int mid=(l+r)>>1;
	build_tree(id*2,l,mid);
	build_tree(id*2+1,mid+1,r);
	pushup(id);
}

void update(int id,int l,int r,int L,int R,int z,bool kind){
	if(r<L||R<l) return;
	if(L<=l&&r<=R){
		if(kind) tree[id].val2=(tree[id].val2+z)%mod;
		if(kind) tree[id].val3=(tree[id].val3+tree[id].val1*z%mod)%mod;
		tree[id].val4=(tree[id].val4+tree[id].val1*z%mod)%mod;
		if(kind) tree[id].lazy+=z;
		return;
	}
	pushdown(id);
	int mid=(l+r)>>1;
	if(L<=mid) update(id*2,l,mid,L,R,z,kind);
	if(R>mid) update(id*2+1,mid+1,r,L,R,z,kind);
	pushup(id);
}

int query(int id,int l,int r,int L,int R,int type){
	if(r<L||R<l) return 0;
	if(L<=l&&r<=R){
		if(type==1) return tree[id].val1;
		if(type==2) return tree[id].val2;
		if(type==3) return tree[id].val3;
		if(type==4) return tree[id].val4;
	}
	pushdown(id);
	int res=0,mid=(l+r)>>1;
	if(L<=mid){
		int val=query(id*2,l,mid,L,R,type);
		res=(res+val)%mod;
	}
	if(R>mid){
		int val=query(id*2+1,mid+1,r,L,R,type);
		res=(res+val)%mod;
	}
	return res;
}

int ask(int x,int y,int type){
	int res=0;
	while(top[x]!=top[y]){
		if(Dep[top[x]]<Dep[top[y]]) swap(x,y);
		res=(res+query(1,1,cnt,dfsnum[top[x]],dfsnum[x],type))%mod;
		x=fa[top[x]];
	}
	if(Dep[x]<Dep[y]) swap(x,y);
	res=(res+query(1,1,cnt,dfsnum[y],dfsnum[x],type))%mod;
	return res;
}

int lca(int x,int y){
	while(top[x]!=top[y]){
		if(Dep[top[x]]<Dep[top[y]]) swap(x,y);
		x=fa[top[x]];
	}
	if(Dep[x]<Dep[y]) swap(x,y);
	return y;
}

int work(int x,int y){
    //照着式子计算即可。
	int res=0,lc=lca(x,y);
	int sum=(g+query(1,1,cnt,dfsnum[y],dfsnum[y],2))%mod;
	int val=(ask(x,y,1)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],1)+mod)%mod;
	res=(res+sum*val%mod)%mod;
	res=(res+ask(x,lc,4)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],4)+mod)%mod;
	res-=2ll*query(1,1,cnt,dfsnum[lc],dfsnum[lc],2)%mod*
    ((ask(x,lc,1)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],1)+mod)%mod)%mod;
	res=(res+mod)%mod;
	res-=(ask(lc,y,3)-query(1,1,cnt,dfsnum[lc],dfsnum[lc],3)+mod)%mod;
	res=(res+mod)%mod;
	return (res+mod)%mod;
}

signed main(){
	read(n,g);
	for(int i=1;i<n;i++){
		int a,b,d,t;
		read(a,b,d,t);
		build(a,b,d,t);
		build(b,a,d,t);
		mp[make_pair(a,b)]=mp[make_pair(b,a)]=t;
	}
	dfs(1,1);
	dfs2(1,1);
	build_tree(1,1,cnt);
	read(q);
	for(int i=1;i<=q;i++){
		int opt,x,y,t;
		read(opt);
		if(opt==0){
			read(x,y,t);
			if(Dep[x]<Dep[y]) swap(x,y);
			int val=t-mp[make_pair(x,y)];
			mp[make_pair(x,y)]=mp[make_pair(y,x)]=t;
			update(1,1,cnt,dfsnum[x],dfsnum[x]+siz[x]-1,val,true);
			update(1,1,cnt,dfsnum[x],dfsnum[x],-val,false);
            //只有x这个点的父亲没有修改，单独处理。
		}
		if(opt==1){
			read(x,y);
			cout<<work(x,y)<<'\n';
		}
	}
	return 0;
}

ID

10539

时间

2000ms

内存

256MiB

难度

标签

递交数

已通过

上传者

Hydro

1 条题解

自动搬运

以下是正文

前言

思路

代码

[NOISG 2021 Qualification] Truck

信息

1 条题解

自动搬运

以下是正文

前言

思路

代码

[NOISG 2021 Qualification] Truck

信息

还没有账户？

登录