自动搬运

查看原文

来自洛谷，原作者为

	fairytale 不要忘记我们的歌

搬运于2025-08-24 23:01:03，当前版本为作者最后更新于2024-05-27 22:32:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

记 Alice 所剩的点组成的序列为 $A$，Bob 所剩的点组成的序列为 $B$。

先考虑 Alice 的树已经给出的情况。

我们约定 Bob 对 $i$ 号点进行决策当且仅当 Alice 已经 dfs 完了 Alice 树上 $i$ 号点子树内的所有点。不难发现按照这样的顺序决策符合了字典序贪心的性质。

同时，Bob 不会在一个结点下挂上两个以上的结点。因为假如挂上了多个，那只保留字典序最大的那个一定更优。

这启示我们 Bob 在每个结点挂上的都是一条链。

特殊性质 A

Bob 的策略在 Alice 树给定时就很明显了：

考虑 Alice 最后 dfs 的过程，因为字典序和排列的特性，Alice 的路径一定是唯一的。

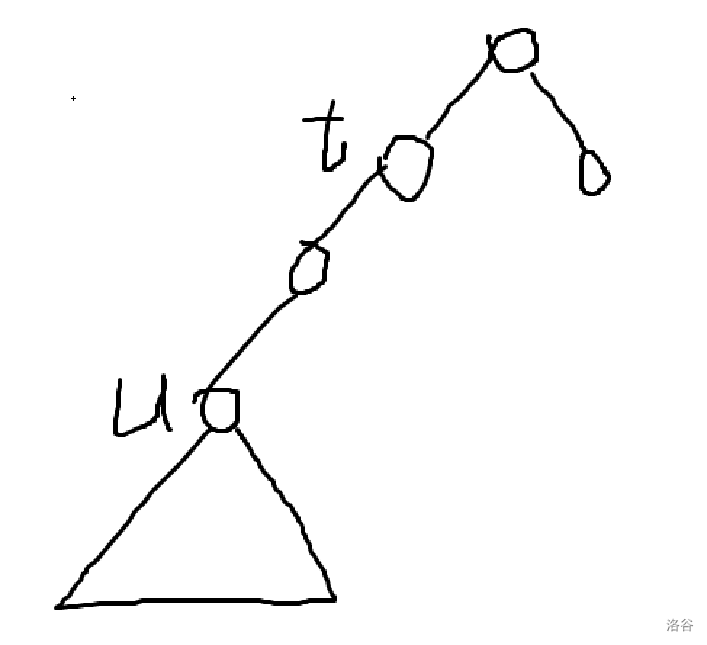
假设 Bob 在决策点 $u$，Alice 树中下一个加入序列的点已经确定了，记它的权值为 $nxt$，同时考虑 $u$ 往上跳到的最后一个没有分叉的点 $t$，则除 $t$ 以外，Bob 在 $u$ 到 $t$ 这条链上挂的每一条链中的结点都是当时 $B$ 中所剩的权值最大的点，而 $t$ 挂的是 $B$ 中所剩的字典序最大的下降子序列。当然，还要时刻满足这个点挂上去之后不会成为权值更小的儿子，并且权值 $>nxt$。

这些决策可以用线段树快速维护出来。

正解

现在考虑无特殊性质的情况。

我们跟随 Alice 的视角进行 dfs，同时处理 Bob 的决策。

假设现在考虑到点 $u$，若 $A$ 中能放的最小权值小于 $B$ 中能放的最大权值，那就一定会给 $u$ 挂上儿子，然后 dfs 这个儿子。

考虑 $u$ 没有要挂的儿子的情况。此时轮到 Bob 进行决策，现在没有了特殊性质 A，就代表我们不知道 Alice 下一个没有分叉的点在哪里和它的权值是多少。

但是我们可以用队列先把这些等待挂上链的结点记录下来，然后回溯到父亲，一直到 $A$ 中能放的最小权值小于 $B$ 中能放的最大权值为止。此时，Alice 下一个点的权值至多是 $A$ 中能放的最小权值。

于是我们可以像特殊性质 A 一样处理队列里点的决策。最终要么队列被清空，要么 $B$ 中能放的最大权值小于 $A$ 中能放的最小权值。发现这两种情况都是刚刚讨论过的，队列被清空就可以给 Alice 挂上儿子继续 dfs，否则回溯到父亲即可。

注意根结点要特殊处理一下。

代码写得比较丑，看着很长其实很多地方逻辑是重合的，代码大差不差。应该有更加简洁的实现（

#include<bits/stdc++.h>
bool st;
#define ls ((p)<<1)
#define rs (((p)<<1)|1)
#define mid ((l+r)>>1)
#define rep(x,qwq,qaq) for(int (x)=(qwq);(x)<=(qaq);++(x))
using namespace std;
#define maxn 200100
int n,m;
int a[maxn];
int fa[maxn];
int inv[maxn];
int mx[maxn<<2],mn[maxn<<2];
void build(int p,int l,int r) {
	if(l==r)return void(mx[p]=mn[p]=a[l]);
	build(ls,l,mid),build(rs,mid+1,r);
	mx[p]=max(mx[ls],mx[rs]);
	mn[p]=min(mn[ls],mn[rs]);
}
void modify(int p,int l,int r,int x) {
	if(l==r)return mx[p]=0,mn[p]=n+n+1,void();
	if(x<=mid)modify(ls,l,mid,x);
	else modify(rs,mid+1,r,x);
	mx[p]=max(mx[ls],mx[rs]);
	mn[p]=min(mn[ls],mn[rs]);
}
int query(int p,int l,int r,int L,int R) {
	if(L>R)return (R<=n?n+n+1:0);
	if(L<=l&&r<=R)return (R<=n?mn[p]:mx[p]);
	int res=(R<=n?n+n+1:0);
	if(L<=mid)res=(R<=n?min(res,query(ls,l,mid,L,R)):max(res,query(ls,l,mid,L,R)));
	if(mid<R)res=(R<=n?min(res,query(rs,mid+1,r,L,R)):max(res,query(rs,mid+1,r,L,R)));
	return res;
}
void clr(int x) {
	modify(1,1,n+n,x);
}
int getnxt(int x) { //返回 pos
	if(x<=n)return inv[query(1,1,n+n,x+1,n)];
	else {
		if(x==n+n+1)x=n;
		return inv[query(1,1,n+n,x+1,n+n)];
	}
}
bool vis[maxn];
int mson[maxn];//mson[i] 表示 i 字典序最大的 Alice 结点儿子 
int lst[maxn];
queue<int>q;
void dfs(int u) {
	int a_first=getnxt(u),b_first=getnxt(n+n+1);
	for(; a[a_first]<a[b_first]||(u==1&&a_first); a_first=getnxt(u),b_first=getnxt(n+n+1)) {
		if(a[a_first]>=a[b_first])while(!q.empty())q.pop();
		int f=(q.size()?q.front():0);
		if(f&&lst[f]&&b_first>lst[f]) {//直接接在当前正在构造的链下面 
			fa[b_first]=lst[f],lst[f]=b_first;
			clr(b_first);
		} else if(f&&!lst[q.back()]&&a[mson[q.back()]]<a[b_first]) {//新开一条链 
			while(q.size()) {
				f=q.front();
				if(lst[f]||a[mson[f]]>a[b_first]) {
					q.pop();
				} else break;
			}
			fa[b_first]=f,lst[f]=b_first;
			clr(b_first);
		} else if(f&&a[getnxt(lst[f])]>a[a_first]) {//字典序最大的下降子序列 
			int k=getnxt(lst[f]);
			fa[k]=lst[f],lst[f]=k;
			clr(k);
		} else {
			fa[a_first]=u;
			mson[u]=a_first;
			clr(a_first);
			while(!q.empty())q.pop();
			dfs(a_first);
		}
	}
	q.push(u);
}
vector<int>g[maxn];
int dep[maxn];
void prt(int u) {
	cout<<a[u]<<" ";
	dep[u]=dep[fa[u]]+1;
	for(int v:g[u]) {
		prt(v);
	}
}
void out() {
	rep(i,2,n+n) {
		g[fa[i]].emplace_back(i);
	}
	rep(i,1,n+n)sort(g[i].begin(),g[i].end(),[](int x,int y) {
		return a[x]<a[y];
	});
	prt(1);
	cout<<'\n';
}
bool ed;
signed main() {
	cerr<<(&st-&ed)/1024.0/1024.0<<" MB\n";
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int T;
	cin>>T;
	cin>>n;
	rep(i,1,n+n)cin>>a[i];
	a[0]=n+n+1;
	rep(i,0,n+n+1)inv[a[i]]=i;
	build(1,1,n+n);
	rep(i,1,n)mson[i]=n+n+1;
	dfs(1);
	int lst=0;
	while(!q.empty()) {
		int t=q.front();
		q.pop();
		int x=getnxt(n+n+1);
		int Lim=a[mson[t]];
		if(a[x]<=Lim)continue;
		fa[x]=t;
		clr(x);
		lst=x;
		int k=getnxt(n+n+1);
		while(k>x&&k!=n+n+1) {
			fa[k]=x,x=k;
			clr(k);
			lst=x;
			k=getnxt(n+n+1);
		}
	}
	if(lst) {
		int x=lst,t=lst;
		while(1) {
			x=getnxt(x);
			if(x==n+n+1)break;
			fa[x]=t,t=x;
			clr(x);
		}
	}
	out();
	return 0;
}