自动搬运

查看原文

来自洛谷，原作者为

	Ratio_Y 善于隐藏自己的精明，才称得上是最大的精明。——拉罗什福科《道德箴言录》||主页跳转https://www.luogu.com.cn/paste/gaajjpsj

搬运于2025-08-24 23:01:02，当前版本为作者最后更新于2024-07-14 08:21:45，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一道比 T2 简单的 T3。

思路

我们发现比赛流程图的形状是一棵完全二叉树，而题目所求的出每一轮次的进入范围限制也是从它的子比赛更新而来的，因此可以按类似线段树建图的方法直接处理出每一轮次的范围，最后 $O(1)$ 查询即可。

我们先设 $l_i$，$r_i$ 分别为第 $i$ 个节点中至少有 $l_i$ 个数比符合条件的值 $x$ 小，至少有 $r_i$ 个数比 $x$ 大。

放一张图形式化一下：

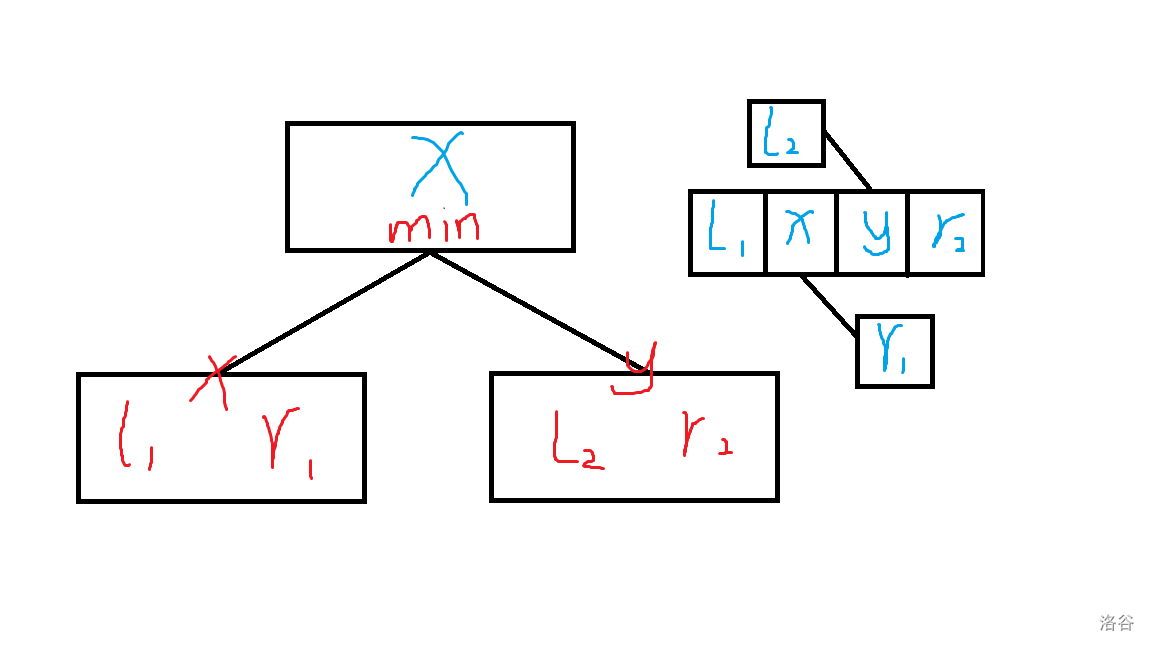
（图丑，轻喷）

我们以一个按照规则二比赛的节点举例：假设胜者为 $x$，那么比赛后即拼凑后的范围块长右图那样。

更新时，首先已知有 $r_1$ 个数需要比 $x$ 大，有 $r_2$ 个数需要比 $y$ 大，同时要满足 $x<y$，所以最终这一节点的 $r_i$ 值应为 $r_1+r_2+1$；

同时需要至少有 $l_1$ 个数比 $x$ 小，$l_2$ 个数比 $y$ 小，由获胜者为 $x$ 我们可以推出 $l_1<l_2$，即 $x$ 能取到更小的值，所以在这个节点中的左边界就是 $x$ 子节点的左边界，但这是在假设 $x$ 获胜的情况，所以真正更新时的 $l_i$ 应等于 $\min(l_1,l_2)$。

按规则一比赛的节点同理，大家可以自己手动模拟下，最终转移式为：

实现方面，由于二叉树的性质，我们根据节点长度 $len$ 可知该节点所在的层数为 $\log \,len$。题目中只需要进入某一层即可，所以整层的范围就是该层所有块的左右边界值分别的最小值。

细节处理

每节点左右边界初始为 $0$ 即无限制，每层左右边界初始为 $+\infty$ 以便赋值。

更新左右边界时要先递归到叶子结点再更新，因为每节点长度是从大到小的，而我们需要由小节点推大节点。

题目询问中为轮数，转化为层数需要在输入时减去 $1$。

Code：

#include<bits/stdc++.h>

using namespace std;

const int Ratio=0;
const int N=1e6+5;
const int maxx=2e9;
int n,m;
int v[N<<1],sl[N<<1],sr[N<<1],L[25],R[25];

namespace Wisadel
{
	#define ls (rt<<1)
	#define rs (rt<<1|1)
	#define mid ((l+r)>>1)
	void Wbuild(int rt,int l,int r)
	{
		if(l==r) return;
		int ceng=log2(r-l+1);// log2 自动向下取整 
		Wbuild(ls,l,mid),Wbuild(rs,mid+1,r);
		
		if(v[rt]==1) sl[rt]=sl[ls]+sl[rs]+1,sr[rt]=min(sr[ls],sr[rs]);
		else sl[rt]=min(sl[ls],sl[rs]),sr[rt]=sr[ls]+sr[rs]+1;
		// 判断节点类型并进行更新 
			
		L[ceng]=min(L[ceng],sl[rt]),R[ceng]=min(R[ceng],sr[rt]);
		// 更新每层范围 
	}
	short main()
	{
		scanf("%d%d",&n,&m);
		for(int i=1;i<=(1<<n)-1;i++) scanf("%d",&v[i]);
		for(int i=1;i<=n;i++) L[i]=maxx,R[i]=maxx;
		Wbuild(1,1,(1<<n));
		
		for(int i=1;i<=m;i++)
		{
			int a,b;scanf("%d%d",&a,&b);b-=1;
			if(a>L[b]&&(1<<n)-a>=R[b]) printf("Yes\n");
			// 判断是否在范围内
			// (1<<n)-a>=R[b] 即为 (1<<n)-a+1>R[b] 
			else printf("No\n");
		}
		return Ratio;
	}
}
int main(){return Wisadel::main();}