自动搬运

查看原文

来自洛谷，原作者为

	zzlzk **

搬运于2025-08-24 21:20:36，当前版本为作者最后更新于2017-08-26 21:09:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

• LaTex写公式有点麻烦，所以我用以前写好的代替了

• 想看原版可以戳这里

• 首先来分析一下这个题目

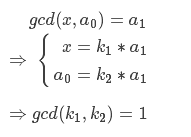
证明:

• 把上面的结论推广一下，得到结论$P$

对于两个正整数$a,b$，设$gcd(a,b)=k$，则存在$gcd(a/k,b/k)=1$

• 应用结论$P$

• 整理一下式子

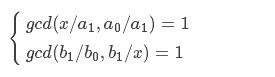
用心体会这两个式子，你会发现$x$是$a_1$的整数倍而且是$b_1$的因子

~~好像这个由gcd和lcm也可以得到？~~嗯，就这样

于是得到一种解题思路

$\sqrt b_1$枚举$b_1$的因子(也就是$x$)，如果这个数是$a_1$的整数倍并且满足那两个式子，则$ans++$

• code

#include<cstdio>
using namespace std;
int gcd(int a,int b) {
    return b==0?a:gcd(b,a%b);
}
int main() {
    int T;
    scanf("%d",&T);
    while(T--) {
        int a0,a1,b0,b1;
        scanf("%d%d%d%d",&a0,&a1,&b0,&b1);
        int p=a0/a1,q=b1/b0,ans=0;
        for(int x=1;x*x<=b1;x++) 
            if(b1%x==0){
                if(x%a1==0&&gcd(x/a1,p)==1&&gcd(q,b1/x)==1) ans++;
                int y=b1/x;//得到另一个因子
                if(x==y) continue; 
                if(y%a1==0&&gcd(y/a1,p)==1&&gcd(q,b1/y)==1) ans++;
            }
        printf("%d\n",ans);
    }
    return 0;
}