自动搬运

查看原文

来自洛谷，原作者为

	WZWZWZWY 一只蜷缩在只因房里敲代码的蒟蒻（真）|| ╯ω╰ || 这只蒟蒻已经被滚去学whk了qwq

搬运于2025-08-24 23:00:32，当前版本为作者最后更新于2024-07-08 08:08:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

啊吧啊吧，被打回了。原因是“大数字应使用科学计数法表示”，于是我改成了 $mod=10^9+7$。（话说 $1e9+7$ 不是科学计数法吗？）

---

从下往上看↑（真实事件未改编）

---

题意避坑

这道题坑也是非常的多。

一：

目标是在恰好两步内获得尽可能多的星星，然而小 S 不会玩，于是每次就会随意挑选一个可以移动到的新位置进行移动。

前一句话我给她划掉了，因为这是误导句。后面一句才是重点，千万不要用正常人玩游戏的思维！

小 S 随意移动。

• 不需要找尽可能多的星星。

二：

每次操作，你可以将捕捉器移动到同行或同列的某个位置，使得新位置与原位置不同且必须保证新位置 $(x',y')$ 满足 $1\leq x'\leq n$，$1\leq y'\leq m$。捕捉器会捕捉 $(x,y)$ 到 $(x',y')$ 路径上所有的星星。一个星星被捕捉后将会消失。

• 也就是说，你每次可以上下左右移动任意格，就像象棋里的车。但是每次必须移动，移动两次。这路上经过的所有星星都会被吃掉。

比如可以这么移动：

$$(1,1)\to(1,2)\to(1,3)$$

这就算两步。是一个方向也可以。（因为小 S 不会玩啊，随意移动）

那么小 S 还可以有什么操作呢？

初始点 $(1,2)$，有星星的点 $(1,3)$。

$$(1,2)\to(1,1)\to(1,3)$$ $$(1,2)\to(1,3)\to(1,1)$$

都可以。

还有，注意到新位置 $(x',y')$ 满足 $1\leq x'\leq n$，$1\leq y'\leq m$。也就是说：

• 地图的最小坐标是 $(1,1)$，而不是 $(0,0)$。

三：

$(x,y)\neq(p,q)$

$(x,y)$ 是初始点，$(p,q)$ 是有星星的点。也就是说：

• 初始点上不会有星星。

四：

每个位置上可以有多颗星星。

就在“输入格式”里，原话……

目前只记得这些，还有什么容易踩到的坑，欢迎在评论区交流！

---

样例解释

很多人第一个样例都只找到了共 $10$ 颗星星的路径。

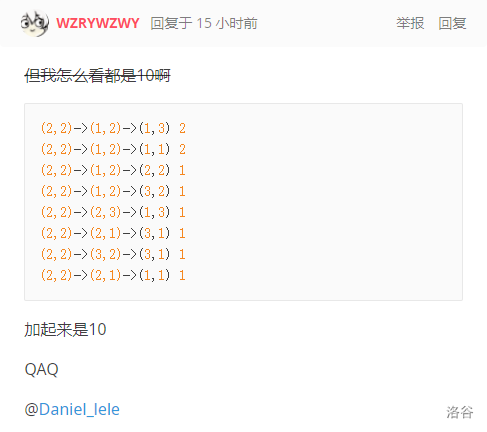
（左边是路径，右边是可以得到的星星数，忽略没有星星的路径。这里少了一条。）

剩下一条，看了上面“避坑”，你应该能找到。

$$(2,2)\to(3,2)\to(1,2)$$

得到 $1$ 颗星星。所有路径总共 $11$ 颗。

---

思路

对于每一颗星星，计算初始点到它的路径数量 $cnt$。最后累加 $cnt$ 计入答案。

---

推导式子

用电脑绘图累死我了，还不快点个赞！

当在同一行或同一列时，拿 $p<x,q=y$ 举例：

首先，第一步只能向左走，对吧？否则两步到不了 $(p,q)$。

若从 $(x,y)$ 第一步走到 $(p,q)$ ，可以上下左右移动任意步（但步数 $>0$，$1\le x'\le n$，$1\le y'\le m$），所以总共有 $(n-1+m-1)$ 种结果。

也可以第一步向左超过 $(p,q)$，这时第二步也是上下左右任意移动,$(n-1+m-1)$ 种结果。

若第一步没有走到 $(p,q)$，或者先向右走，那么第二步必须走到 $(p,q)$，或者超过 $(p,q)$，才能吃到它，总共有 $(n-p-1)\times (p-1)$ 种结果。

那么加起来就有 $(n+m-2 + n-p-1) \times p$ 种结果。

其它三个方向（上、右、下）同理。

---

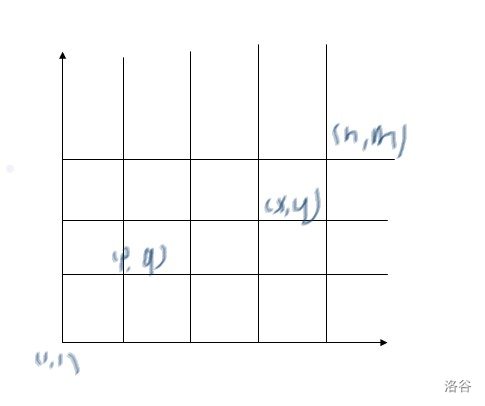
不在同一行或同一列。

拿这个图举例。

显然，有两种路径到达 $(p,q)$，分别是 $(x,y)\to(p,y)\to(p,q)$ 和 $(x,y)\to(x,q)\to(p,q)$。

这个时候已经用了“两步”了，不可能再转向。但是——这个时候最后一步可能没有走完，可以继续往前走。

可以 $(x,y)\to(p,y)\to(p,1)$。

那么显然地，最后一步向下的方案数为 $q$，向左的方案数为 $p$。

总的方案数是 $p+q$。

其他方向同理。

---

代码

忠告：$mod=10^9+7$ 不要取错。每次乘法都要取模。$1\leq n,m\leq10^{18}$，不开 long long 见祖宗。

（考场代码，保险起见都加上了取模。可能稍微合并了一些公式。）

cin >> p >> q; // 每个星星的横、纵坐标
int cnt = 0;
if (p < x) { // 横坐标比初始点横坐标小
	if (q < y) cnt = p % mod + q % mod; // 纵坐标比初始点小
	if (q > y) cnt = (m-q+1) % mod + p % mod; // 纵坐标比初始点大
	if (q == y) cnt = (n+m-2 + n-p-1) % mod * (p % mod) % mod; // 纵坐标相等
} else if (p > x) {
	if (q < y) cnt = q % mod + (n-p+1) % mod;
	if (q > y) cnt = (m-q+1) % mod + (n-p+1) % mod;
	if (q == y) cnt = (n-p+1) % mod * ((n+m-2 + p-2) % mod);
} else { // 横坐标相等
	if (q > y) cnt = (m-q+1) % mod * (((n+m-2) % mod + q-2) % mod);
	else cnt = q % mod * ((m+n-2 + m-q-1) % mod);
}
ans += cnt;

还有什么不懂的或者想吐槽的可以在评论区讨论。