自动搬运

查看原文

来自洛谷，原作者为

	Cells 成功的秘诀只有™一个：加训。

搬运于2025-08-24 23:00:23，当前版本为作者最后更新于2025-01-17 13:11:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P10700 [SNCPC2024] 猜质数 II 嚼烂喂到嘴里教学

前言

一道很典的题，感谢 @ why @ tiansuohaoer @ maniubi @ Cobal @ dayz_break 提供大力帮助。

思路

首先先读 $10$ 分钟题，然后手模第一组样例的第一个询问，确保读懂题意，否则嚼得再烂都没用。

我们先将题目中乱七八糟的定义揉到一起，得到这个式子：

$$\displaystyle \sum_{i = 1}^{10^6} \sum_{j = l}^{r} f(i, a_j) $$

然后我们换个枚举顺序：

$$\displaystyle \sum_{i = l}^{r} \sum_{j = 1}^{10^6} f(j, a_i) $$

其中

$$f(x,y)= \left\{\begin{array}{rcl}u-y, & x=1 \\ u, & 1<x\le y,\ \gcd(x,y)=1 \\ -x\cdot y, & x\neq 1,\ \gcd(x,y)=x \\ 0, & \text{otherwise} \end{array}\right. $$

你看看函数 $f$ 第二个的式子，当 $x$ 与 $y$ 互质且 $1 < x \le y$ 时，函数值是 $u$，那么这一种情况之和就是 $u \times \varphi(y)$。第三个式子，当 $x$ 是 $y$ 的因数且 $x \not = 1$ 时，是 $-x \times y$，所以第二种情况之和就是 $y$ 的因子和与 $y$ 的乘积的相反数，即 $- \displaystyle \sum_{x \mid y} x \times y$。你可能会好奇为什么有第一个式子，因为当 $x = 1$ 时，第二三个式子（不要前面的那一个不等式）都是成立的，所以这个玩意的函数值就是 $u \times 1 - 1 \times y = u - y$，这也是为什么第二个式子的条件是 $1 < x \le y$，第三个式子的条件是 $x \not = 1$ 了。

综上所述，我们可以将式子化为：

$$\displaystyle \sum_{i = l}^{r} u \times \varphi(a_i) - num_{a_i} $$

其中 $num_{a_i}$ 就是 $\displaystyle \sum_{x \mid y} x \times y$。告诉 $a_i$，线性筛可以预处理得到 $\varphi$ 值，然后预处理出 $num$ 数组（因数和的与数的乘积）。

给定 $l, u$，求最大的 $r$，使得上面的函数值最大。我们发现可以使用前缀和处理掉 $l$ 到 $r$ 的循环，于是：

$$u \times (prephi_{r} - prephi_{l - 1}) - (sum_{r} - sum_{l - 1}) $$

$prephi_{x}$ 就是前 $x$ 个 $a_i$ 的 $phi_{a_i}$ 之和，$sum_{x}$ 就是前 $x$ 个 $a_i$ 的 $num_{a_i}$ 的和。

我们为了方便好看，换个名字，将 $prephi$ 看作 $x$，把 $sum$ 看作 $y$，然后再将函数值设为 $b$，就有：

$$u \times (x_{r} - x_{l - 1}) - (y_{r} - y_{l - 1}) = b $$

因为 $l$ 给定，所以说 $x_{l - 1}, y_{l - 1}$ 不变，相当于我们的坐标轴平移了一下，所有点该怎么怎么样，相对位置不会发生改变，我们不妨将其写成：

$$u \times x_{r} - y_{r} = b$$

学过初二的同学都知道一次函数的一般式：

$$y = k \cdot x + b$$

如果你学过斜率优化（不学也没关系）就会更好的理解这里的类比。这不就是一个一次函数吗？移项：

$$y_{r} = u \times x_{r} - b$$

我们要求让 $b$ 最大，那么 $-b$ 就应该最小。每一对 $x, y$ 的值就相当于平面直角坐标系上的一个点，我们相当于是已知一次函数斜率及函数值，求截距，但是如果暴力算的话每一次都是 $O(n)$。那咋搞啊哥？

我们不妨数形结合画个图：

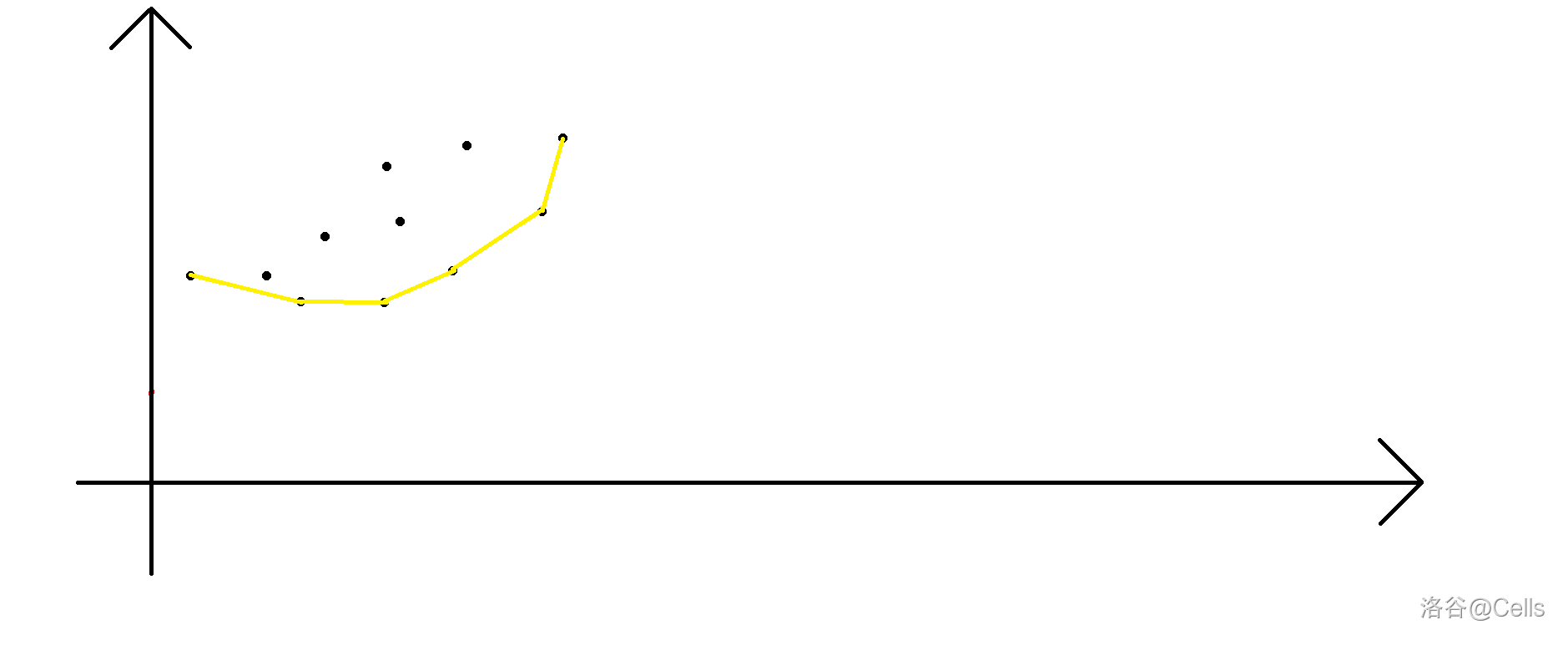
是的，我们发现在凸包内的点无论斜率是多少，都取不到，如果你学过斜率优化 （又来），就更能理解了，如果不会维护凸包就上谷找板子吧，简单来说就是单调栈维护点与点之间的斜率。

另外在这道题中因为斜率始终是正数，所以只需要维护下凸包。但是这样的时间复杂度仍然不算理想，我们通过模拟发现，这不就当于是斜率为 $u$ 的直线去《切》凸包。

观察斜率 $u$ 和切点左右线段的斜率关系。

诶？左边线段的斜率小于 $u$，右边线段的斜率大于 $u$，又因为我们的凸包斜率始终有单调性，所以可以二分 $\log$ 时间查找。

注意 $a_i \le 10^6$，$num$ 数组可能会爆 long long，需要开 __int128，同理前缀和 $x, y$ 数组也会爆。并且由于只给定 $l$，要求区间的右端点 $r$，所以 $l \le r$，但是因为全局的凸包和 $l$ 右边的凸包可能长相不一样（绿色和黄色）：

所以我们需要从后往前遍历边加点，边处理询问，所以需要离线询问并排序。

Code

# include <bits/stdc++.h>
# define int long long
# define fir first
# define sec second
# define vec vector
# define pb push_back
# define mem(a, b) memset(a, b, sizeof(a))
# define rep(i, a, b) for(int i = (a); i <= (b); ++ i)
# define pre(i, a, b) for(int i = (a); i >= (b); -- i)
using namespace std;

using LL = long long;
using PII = pair<int, int>; 

const int N = 5e5 + 10, A = 1e6 + 10;

int n, m, top, tot;
int a[N], stk[N], phi[A], prime[N];
__int128 x[N], y[N], num[A];

vec<PII> q[N]; 

PII answer[N]; 

int calc(int u, int l, int r){
	return u * (x[r] - x[l - 1]) - (y[r] - y[l - 1]);
}

void sieve(int n){
	rep(i, 1, n){
		for(int j = i; j <= n; j += i){//预处理因子和 
			num[j] += i;
		}
	}
	
	phi[1] = 1;//线性筛的时候处理phi
	rep(i, 2, n){
		if(!phi[i]) prime[++ tot] = i, phi[i] = i - 1;
		
		for(int j = 1; prime[j] * i <= n; j ++){
			if(i % prime[j] == 0){
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	
	sieve(A - 10);
	
	cin >> n >> m;
	rep(i, 1, n) cin >> a[i];
	
	rep(i, 1, n){//处理phi和因子和与数乘积的前缀和 
		x[i] = phi[a[i]] + x[i - 1];
		y[i] = a[i] * num[a[i]] + y[i - 1];
	}
	
	rep(i, 1, m){
		int u, l;
		cin >> u >> l;
		q[l].pb({u, i});//离线询问桶排 
	}
	
	pre(i, n, 1){//从后往前 
		while(top > 1 && (y[stk[top]] - y[stk[top - 1]]) * (x[i] - x[stk[top - 1]]) < (y[i] - y[stk[top - 1]]) * (x[stk[top]] - x[stk[top - 1]])) top --;//维护下凸包 
		stk[++ top] = i;//这里的i和离线是的l都是a数组的编号，所以是相同的含义 
		
		rep(j, 0, (int)q[i].size() - 1){
			int u = q[i][j].fir, id = q[i][j].sec;
			int l = 1, r = top - 1, res = top;//因为l = top - 1，所以说top需要单独计算
			while(l <= r){
				int mid = l + r >> 1;
				if((y[stk[mid]] - y[stk[mid + 1]]) < u * (x[stk[mid]] - x[stk[mid + 1]])) r = mid - 1, res = mid;//建议手模这个过程，注意栈中的编号是反着的 
				else l = mid + 1;
			}
			
			int ans = calc(u, i, stk[res]), pos = stk[res];
			answer[id] = {ans, pos};
		}
	}
	
	rep(i, 1, m) cout << answer[i].fir << " " << answer[i].sec << "\n";
	
	return 0;
}

写这篇题解一是教练压力的，另一个确实这题很好，我自己的计算几何里面凸包等玩意也没学好，写一下也能加深印象，这篇题解就到这里，感谢你的观看 QwQ。