1 条题解

  • 0
    @ 2025-8-24 23:00:17

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar microchip
    只会打数据结构的屑芯片QAQ || 遗憾离场 || 宣传DS题单QwQ：https://www.luogu.com.cn/training/588263

    搬运于2025-08-24 23:00:17，当前版本为作者最后更新于2024-07-19 15:36:07，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    题意翻译：

    你需要维护一个序列，支持以下操作：

    ADD x y D 将序列中第 xx 到 yy 个元素加 dd .

    REVERSE x y 将序列中第 xx 到 yy 个元素进行区间翻转操作.

    REVOLVE x y D 定义右移操作为将某个区间的最后一个元素移动到该区间的最前面，将序列中第 xx 到 yy 个元素所在的区间进行 dd 次右移操作.

    INSERT x P 将元素 PP 插入到序列中第 xx 个元素的后面.

    DELETE x 删除序列中第 xx 个元素.

    MIN x y 求序列中第 xx 到 yy 个元素的最小值.

    Solution：伸展树

    众所周知，对于复杂的序列维护问题（如区间翻转），我们常用平衡树来维护.常用的序列平衡树有两种：Splay Tree 和 FHQ Treap.

    这里我们使用 Splay 来解决此题.

    阅读前请先使用 Splay 完成 普通平衡树 和 文艺平衡树 来熟悉 Splay 的基本操作，以及如何使用 Splay 来处理区间操作，本题解默认您已经了解这些内容.

    Step 1：建树

    最简单粗暴的办法是以 nlog⁡nn \log n 的复杂度依次对每个元素执行插入操作，但我们有更高明的办法：

    void build(int l,int r,int &no,int a[]){
	if(l>r)return;
  	if(no==0)no=++nth;
	int mid=(l+r)/2;
	Tr[no].val=a[mid];
	Tr[no].min_val=Tr[no].val;
	build(l,mid-1,Tr[no].left,a);
	if(Tr[no].left){
		Tr[Tr[no].left].fa=no;
		Tr[no].min_val=min(Tr[no].min_val,Tr[Tr[no].left].min_val);
	}
	build(mid+1,r,Tr[no].right,a);
	if(Tr[no].right){
		Tr[Tr[no].right].fa=no;
		Tr[no].min_val=min(Tr[no].min_val,Tr[Tr[no].right].min_val);
	}
	update(no);
}

    这里是将原有数列直接构造成一个完美的平衡树，每次选取数列的中位数作为根，将左半部分作为左儿子，右半部分作为右儿子，递归建树，这样建树的复杂度是 O(n)O(n).

    同时我们给每个节点维护了该点代表区间的最小值，用于查询 RMQ.

    注意要在序列的头和尾多加一个元素，保证不出现越界问题.

    Step 2：查询区间最小值

    通过文艺平衡树一题，我们知道 Splay 提取区间 [l,r][l,r] 的方式是先将 l−1l-1 旋转至根处，再将 r+1r+1 旋转至根下，这样根节点的右子树的左子树就代表了区间 [l,r][l,r].

    问题在于在旋转的过程中，被旋转的点所代表的区间会变化，所以在旋转的过程中我们要注意区间最小值的更新.

    先考虑左旋，如下图：

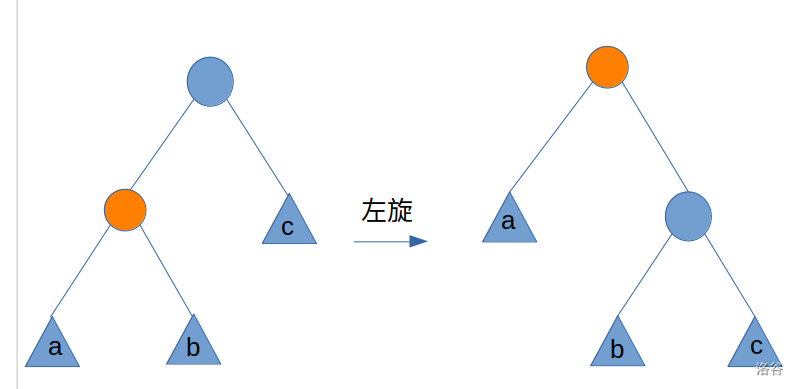
    橙色是我们要向上旋转的一个节点，我们发现该节点所代表的区间变成了其父节点所代表的区间，而父节点所代表的区间变成了 bb 子树和 cc 子树的区间外加自己.

    于是我们在原有旋转代码之中加上这样一个更新操作即可：

    Tr[no].min_val=Tr[tmp].min_val;// tmp 表示 no 的父节点

Tr[tmp].min_val=min(Tr[tmp].val,min(Tr[Tr[tmp].right].min_val,Tr[Tr[no].right].min_val));

    右旋操作同理.

    这样我们就可以查询任意区间的最小值了.

    Step 3：修改操作

    插入和删除是平衡树的基操，这里不再赘述.

    翻转操作和区间加操作通过延时标记来高效解决，相信过了文艺树的您肯定可以很快写出来.

    注意每次旋转操作和查询第 k 个元素时都要将遍历到的点进行标记下传.代码如下：

    void tag_pushdown(int no){
	if(Tr[no].tag_rev){//翻转标记
		swap(Tr[no].left,Tr[no].right);
		Tr[Tr[no].left].tag_rev^=1;
		Tr[Tr[no].right].tag_rev^=1;
		Tr[no].tag_rev=0;
	}
	if(Tr[no].tag_add){//加法标记
		Tr[Tr[no].left].val+=Tr[no].tag_add;
		Tr[Tr[no].left].min_val+=Tr[no].tag_add;
		Tr[Tr[no].left].tag_add+=Tr[no].tag_add;
		Tr[Tr[no].right].val+=Tr[no].tag_add;
		Tr[Tr[no].right].min_val+=Tr[no].tag_add;
		Tr[Tr[no].right].tag_add+=Tr[no].tag_add;
		Tr[no].tag_add=0;
	}
}

void range_rev(int l,int r){
	kth_num(r+2);
	int tmp=root;
	kth_num(l);
	splay_under_root(tmp);
	Tr[Tr[Tr[root].right].left].tag_rev^=1;
	tag_pushdown(Tr[Tr[root].right].left);
}
void range_add(int l,int r,int val){
	kth_num(r+2);
	int tmp=root;
	kth_num(l);
	splay_under_root(tmp);
	Tr[Tr[Tr[root].right].left].tag_add+=val;
	Tr[Tr[Tr[root].right].left].min_val+=val;
	Tr[Tr[Tr[root].right].left].val+=val;
}

    区间右移操作可以等价于区间移动操作，显然，如果移动的步数等于区间长度，那么就相当于没有操作，所以我们先将 DD 对 y−x+1y-x+1 取模，此时就相当于将区间 [x,y−D][x,y-D] 移动到区间 [y−D+1,y][y-D+1,y] 的后方.

    代码如下：

    void range_mov(int l,int r,int stp){
	kth_num(r-stp+2);
	int tmp=root;
	kth_num(l);
	splay_under_root(tmp);
	int Root=Tr[Tr[root].right].left;
	Tr[Tr[root].right].left=0;
	Tr[Tr[root].right].siz-=Tr[Root].siz;
	Tr[root].siz-=Tr[Root].siz;
	kth_num(l+stp+1);
	int tmp2=root;
	kth_num(l+stp);
	splay_under_root(tmp2);
	Tr[Tr[root].right].left=Root;
	Tr[Tr[root].right].siz+=Tr[Root].siz;
	Tr[root].siz+=Tr[Root].siz;
	Tr[Root].fa=Tr[root].right;
}

    于是这道题就解决啦.

    AC 代码如下，使用 class 封装的伸展树（码风有点抽象，见谅）：

    #include<iostream>
using namespace std;

class Splay_Tree{
	private:
		struct node{
			long long val,tag_add,min_val;
			int fa,left,right,siz;
			bool tag_rev;
		}Tr[200050];
		int root,nth,x,k;
	public:
		long long min(long long x,long long y){
			return x<y?x:y;
		}
		bool son(int no){
			return Tr[Tr[no].fa].right==no;
		}
		void update(int no){
			Tr[no].siz=Tr[Tr[no].left].siz+1+Tr[Tr[no].right].siz;
		}
		void tag_pushdown(int no){
			if(Tr[no].tag_rev){
				swap(Tr[no].left,Tr[no].right);
				Tr[Tr[no].left].tag_rev^=1;
				Tr[Tr[no].right].tag_rev^=1;
				Tr[no].tag_rev=0;
			}
			if(Tr[no].tag_add){
				Tr[Tr[no].left].val+=Tr[no].tag_add;
				Tr[Tr[no].left].min_val+=Tr[no].tag_add;
				Tr[Tr[no].left].tag_add+=Tr[no].tag_add;
				Tr[Tr[no].right].val+=Tr[no].tag_add;
				Tr[Tr[no].right].min_val+=Tr[no].tag_add;
				Tr[Tr[no].right].tag_add+=Tr[no].tag_add;
				Tr[no].tag_add=0;
			}
		}
		void rotate(int no){
			if(no==root)return;
			int tmp=Tr[no].fa;
			tag_pushdown(tmp);
			tag_pushdown(no);
			Tr[no].min_val=Tr[tmp].min_val;
			if(son(no)==0){
				Tr[tmp].min_val=min(Tr[tmp].val,min(Tr[Tr[tmp].right].min_val,Tr[Tr[no].right].min_val));
				Tr[tmp].left=Tr[no].right;Tr[Tr[no].right].fa=tmp;Tr[no].right=tmp;
			}else{
				Tr[tmp].min_val=min(Tr[tmp].val,min(Tr[Tr[tmp].left].min_val,Tr[Tr[no].left].min_val));
				Tr[tmp].right=Tr[no].left;Tr[Tr[no].left].fa=tmp;Tr[no].left=tmp;
			}update(tmp);update(no);
			if(tmp==root){
				root=no;
				Tr[no].fa=0;Tr[tmp].fa=no;
				return;
			}int tmp2=Tr[tmp].fa;
			bool flag=son(tmp);
			Tr[tmp].fa=no;Tr[no].fa=tmp2;
			if(flag==0)Tr[tmp2].left=no;
			else Tr[tmp2].right=no;
		}
		void splay(int no){
			while(no!=root){
				if(Tr[no].fa!=root&&son(no)==son(Tr[no].fa))rotate(Tr[no].fa);
				rotate(no);
			}
		}
		void build(int l,int r,int &no,int a[]){
			if(l>r)return;
			if(no==0)no=++nth;
			int mid=(l+r)/2;
			Tr[no].val=a[mid];
			Tr[no].min_val=Tr[no].val;
			build(l,mid-1,Tr[no].left,a);
			if(Tr[no].left){
				Tr[Tr[no].left].fa=no;
				Tr[no].min_val=min(Tr[no].min_val,Tr[Tr[no].left].min_val);
			}
			build(mid+1,r,Tr[no].right,a);
			if(Tr[no].right){
				Tr[Tr[no].right].fa=no;
				Tr[no].min_val=min(Tr[no].min_val,Tr[Tr[no].right].min_val);
			}
			update(no);
		}
		void prework(int len,int a[]){
			for(int i=0;i<100050;i++)Tr[i].val=Tr[i].min_val=1147483647;
			k=len;
			build(0,len+1,root,a);
		}
		int kth(int no){
			if(no==0)return 0;
			tag_pushdown(no);
			if(Tr[Tr[no].left].siz+1==x){
				splay(no);
				return Tr[root].val;
			}if(Tr[Tr[no].left].siz+1>x)return kth(Tr[no].left);
			x-=Tr[Tr[no].left].siz+1;
			return kth(Tr[no].right);
		}
		int kth_num(int val){
			x=val;
			return kth(root);
		}
		void splay_under_root(int no){
			while(Tr[no].fa!=root){
				if(Tr[Tr[no].fa].fa!=root&&son(no)==son(Tr[no].fa))rotate(Tr[no].fa);
				rotate(no);
			}
		}
		int range_min(int l,int r){
			kth_num(r+2);
			int tmp=root;
			kth_num(l);
			splay_under_root(tmp);
			tag_pushdown(root);
			tag_pushdown(tmp);
			tag_pushdown(Tr[Tr[root].right].left);
			Tr[Tr[root].right].min_val=min(Tr[Tr[root].right].min_val,min(Tr[Tr[Tr[root].right].left].min_val,Tr[Tr[Tr[root].right].right].min_val));
			Tr[root].min_val=min(Tr[root].min_val,min(Tr[Tr[root].left].min_val,Tr[Tr[root].right].min_val));
			return Tr[Tr[Tr[root].right].left].min_val;
		}
		void ins(int pos,int val){
			kth_num(pos+2);
			int tmp=root;
			kth_num(pos+1);
			splay_under_root(tmp);
			Tr[Tr[root].right].left=++nth;
			Tr[nth].val=val;
			Tr[nth].fa=Tr[root].right;
			Tr[nth].min_val=Tr[nth].val=val;
			Tr[nth].siz=1;
			Tr[Tr[root].right].siz++;
			Tr[root].siz++;
		}
		void del(int pos){
			kth_num(pos+2);
			int tmp=root;
			kth_num(pos);
			splay_under_root(tmp);
			Tr[Tr[root].right].left=0;
			Tr[Tr[root].right].siz--;
			Tr[root].siz--;
		}
		void range_mov(int l,int r,int stp){
			kth_num(r-stp+2);
			int tmp=root;
			kth_num(l);
			splay_under_root(tmp);
			int Root=Tr[Tr[root].right].left;
			Tr[Tr[root].right].left=0;
			Tr[Tr[root].right].siz-=Tr[Root].siz;
			Tr[root].siz-=Tr[Root].siz;
			kth_num(l+stp+1);
			int tmp2=root;
			kth_num(l+stp);
			splay_under_root(tmp2);
			Tr[Tr[root].right].left=Root;
			Tr[Tr[root].right].siz+=Tr[Root].siz;
			Tr[root].siz+=Tr[Root].siz;
			Tr[Root].fa=Tr[root].right;
		}
		void range_rev(int l,int r){
			kth_num(r+2);
			int tmp=root;
			kth_num(l);
			splay_under_root(tmp);
			Tr[Tr[Tr[root].right].left].tag_rev^=1;
			tag_pushdown(Tr[Tr[root].right].left);
		}
		void range_add(int l,int r,int val){
			kth_num(r+2);
			int tmp=root;
			kth_num(l);
			splay_under_root(tmp);
			Tr[Tr[Tr[root].right].left].tag_add+=val;
			Tr[Tr[Tr[root].right].left].min_val+=val;
			Tr[Tr[Tr[root].right].left].val+=val;
		}
}T;

int n,a[100050],m,x,y,z;
string op;

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	a[0]=-1147483647;a[n+1]=1147483647;
	T.prework(n,a);
	cin>>m;
	while(m--){
		cin>>op;
		if(op=="ADD"){
			cin>>x>>y>>z;
			T.range_add(x,y,z);
		}
		if(op=="REVERSE"){
			cin>>x>>y;
			T.range_rev(x,y);
		}
		if(op=="REVOLVE"){
			cin>>x>>y>>z;
			z%=y-x+1;
			if(z)T.range_mov(x,y,z);
		}
		if(op=="INSERT"){
			cin>>x>>y;
			T.ins(x,y);
		}
		if(op=="DELETE"){
			cin>>x;
			T.del(x);
		}
		if(op=="MIN"){
			cin>>x>>y;
			cout<<T.range_min(x,y)<<endl;
		}
	}
	return 0;
}

    这道题可以很好地考察你的序列平衡树，细节较多，如果你想透彻平衡树，这道题很值得做.

    题外话

    高级数据结构代码很长，可读性低？这时候就该显示出 class 的威力了！

    我们把封装好的伸展树放在一个头文件里，然后......

    #include<iostream>
#include "Data_Structure.h"
using namespace std;

int n,a[100050],m,x,y,z;
string op;

Splay_Tree T;

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	a[0]=-1147483647;a[n+1]=1147483647;
	T.prework(n,a);
	cin>>m;
	while(m--){
		cin>>op;
		if(op=="ADD"){
			cin>>x>>y>>z;
			T.range_add(x,y,z);
		}
		if(op=="REVERSE"){
			cin>>x>>y;
			T.range_rev(x,y);
		}
		if(op=="REVOLVE"){
			cin>>x>>y>>z;
			z%=y-x+1;
			if(z)T.range_mov(x,y,z);
		}
		if(op=="INSERT"){
			cin>>x>>y;
			T.ins(x,y);
		}
		if(op=="DELETE"){
			cin>>x;
			T.del(x);
		}
		if(op=="MIN"){
			cin>>x>>y;
			cout<<T.range_min(x,y)<<endl;
		}
	}
	return 0;
}

    是不是清爽多了！（滑稽）

    • 1

    SuperMemo

    信息

    ID
    10125
    时间
    1000ms
    内存
    512MiB
    难度
    6
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 22ms