自动搬运

查看原文

来自洛谷，原作者为

	myee 与其诺诺以顺，不若谔谔以昌 | AFO

搬运于2025-08-24 22:59:31，当前版本为作者最后更新于2024-07-07 10:43:37，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

发现洛谷把 bzoj 题给搬了过来，所以我把当时写的题解传过来了。

其实就一缝合题，没啥意思。

---

第一问

考虑对补图跑二分图带权最大独立集。

这一部分可以通过一个人类智慧的网络最大流实现。

0           ->    1  - n        101

1   -   n   ->   n+1 - 2n       inf, 当且仅当补图上有该边时连边

n+1 -  2n   ->    2n+1          100

跑从源点 $S=0$ 到汇点 $T=2n+1$ 的最大流，即最小割。

然后就可以计算出男生、女生人数了。

$101$ 与 $100$ 是为了保证男生数目尽量多。

如下图是样例。

---

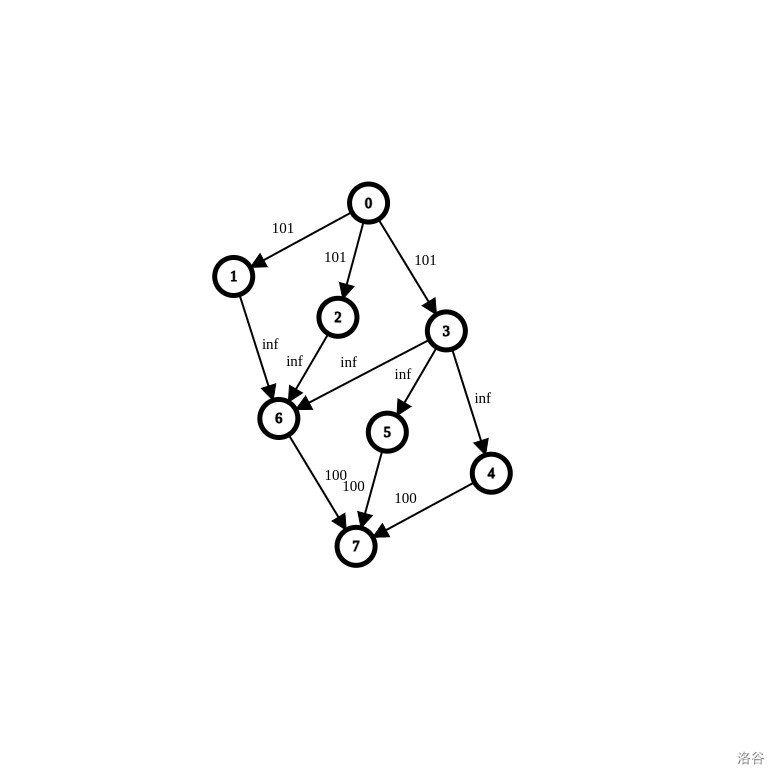
第二问

记 $n$ 个男生，$m$ 个女生的该图中任意挑 $k$ 条边的方案数为 $f_{n,m}=\binom{nm}{k}$，其中符合题目条件的选法有 $g_{n,m}$ 种。

则显然有

$$f_{n,m}=\sum_{a,b}\binom na\binom mbg_{a,b}$$

由二维二项式反演，我们得到

$$g_{n,m}=\sum_{a,b}\binom na\binom mb(-1)^{n+m-a-b}f_{a,b} $$

即答案为

$$\sum_{a,b}\binom na\binom mb\binom{ab}k(-1)^{n+m-a-b} $$

直接做就好了。

---

Code

码头去掉了。

Dinic D;
bol E[55][55];
modint C[5005][5005];
int main()
{
#ifdef MYEE
    freopen("QAQ.in","r",stdin);
#endif
    uint n,k,m;
    scanf("%u%u%u",&n,&k,&m);
    D.build((n+1)<<1);
    for(uint i=1;i<=n;i++)D.insert(0,i,101),D.insert(i+n,n<<1|1,100);
    for(uint i=1;i<=n;i++)for(uint j=1;j<=n;j++)E[i][j]=true;
    while(m--){uint u,v;scanf("%u%u",&u,&v),E[u][v]=false;}
    for(uint i=1;i<=n;i++)for(uint j=1;j<=n;j++)if(E[i][j])D.insert(i,j+n,-1);
    ullt w=201llu*n-D.run(0,n<<1|1);
    uint a=w%100;
    uint b=w/100-a;
    printf("%u %u\n",a,b);
    AnyMod::ChgMod(19921228);
    C[0][0]=1;
    for(uint i=1;i<=5000;C[i][0]=1,i++)for(uint j=1;j<=i;j++)C[i][j]=C[i-1][j-1]+C[i-1][j];
    modint ans;
    for(uint i=0;i<=a;i++)for(uint j=0;j<=b;j++)
        ((i^j)&1)?ans-=C[a][i]*C[b][j]*C[(a-i)*(b-j)][k]:ans+=C[a][i]*C[b][j]*C[(a-i)*(b-j)][k];
    ans.println();
    return 0;
}