自动搬运

查看原文

来自洛谷，原作者为

	听取MLE声一片 如果我当时做的再多一点，结局会不会不同呢？

搬运于2025-08-24 22:58:42，当前版本为作者最后更新于2024-05-19 14:34:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

停车场证明

不难发现最优方案的空地一定呈若干条从出口向外延伸的路径，称一段上下延伸或左右延伸的路径为道路。

对于一段道路而言，宽度一定为 $1$，容易证明为更宽的道路没有意义。

以下红色代表车位，白色代表空地。

定义：拐角、丁字路口、道路末端，分别如下图所示。

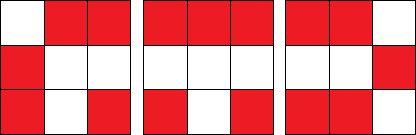
证明答案上界

对于每个空地而言，它旁边可能有零到四个车位。

对于一条道路而言，中间每个空地旁边都有两个车位。不妨假定答案上界为每个空地都与旁边的两个车位对应，也就是每三个位置就有两个是车位。

这样会出现一个疑问，道路末端的空地若不在边界会与三个车位对应，可能会超过设定的上界。

考虑道路的产生条件。若没有丁字路口，全图就只有一个路径，最多只能产生一个道路末端，这样是不影响的。而每增加一个道路末端，就等价于增加了一条支路，也就是多了一个丁字路口。而丁字路口最多只能与一个车位相邻，就抵消了道路末端的贡献。

由此得出空地下界 $\frac{n^2}{3}$，答案上界 $\frac{2n^2}{3}$。

更精确的答案上界

以上情况是理想情况，即为一个空地能与两个车位相邻，但是实际上达不到。

如果一条道路没有分叉且没有改变方向，则这条道路及两侧相邻车位最多只能覆盖 $3n$ 个格子。而连接两个道路必定会造成至少为 $1$ 的车位损耗，称这个损耗为不饱和度。要覆盖所有 $n^2$ 个格子至少需要 $\frac{n^2}{3n}=\frac{n}{3}$ 条路径。

所以有一个更精切的空地下界 $\frac{n^2}{3}+\frac{n}{3}$。

答案上界

定义路块为一段道路及其两侧相邻的车位。若道路长度为 $k$，路块的面积为 $3k$。

对于任意两个路块，应该没有相交的部分；如果相交了，则一个格子与两个空地相邻，一定是不优的。

若不要求各个路块中道路连通，则对原地图进行宽度为 $3$ 的长方形的密铺就是答案。

要求的 $n$ 为 $2023$，其模 $3$ 余 $1$，所以以下只考虑 $n$ 模 $3$ 余 $1$ 的情况。用若干宽度为 $3$ 的长方形去密铺地图，则至少会剩下一个格子。

定义不饱和度为连接两个路块造成的车位损耗，也就是增加一个不饱和度等价于减少一个车位。

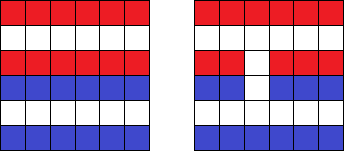
以下图的车位分别用红色和蓝色表示不同路块的车位，黑色为不考虑的部分，左为连接前右为连接后。

拐角如下：

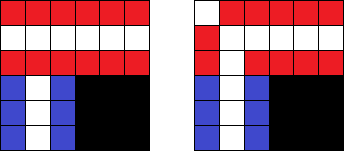
丁字路口如下：

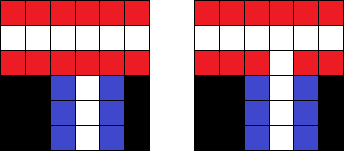
相邻同向如下：

拐角产生的空地如果要消去，需要另外两个方向拼上道路，这样会产生更多的不饱和度，一定不优。之前讨论的道路末尾，如果末尾独占一个位置，则若不覆盖会至少把一个路块分割为两部分，一定不优，

相邻的不同向路块连接可以形成拐角及丁字路口，不饱和度都只有 $1$。而相邻的同向路块连接只能从中间打通需要 $2$ 个不饱和度。

这样没有被路块覆盖的格子应恰好只有一个。若有更多的未覆盖格子，则填上一个路块一定比不填要优。证明为填上一个 $3\times 1$ 的路块会产生 $2$ 个车位并产生 $1$ 个不饱和度，净增加了 $1$ 个车位。

这里相邻的同向路块连接可以通过移动边界处车位来做到 $1$ 个不饱和度，但能转化为不同向的情况，所以不做考虑。

要连接所有的路块，不饱和度至少为路块总数减一。

问题转化为用宽度为 $3$ 的长方形密铺 $n\times n$ 的网格（去掉其中一格），至少要用多少个长方形。

因为 $n$ 不为 $3$ 的倍数所以不能直接铺完，所以两个方向都应该有长方形，至少为 $\frac{2(n-1)}{3}$，最少的不饱和度为 $\frac{2(n-1)}{3}-1$。

因为 $n^2$ 不是 $3$ 的倍数，所以一个空地对应两个车位的分组最多只能分 $\frac{n^2-1}{3}$ 组，也就是这一部分有 $\frac{n^2-1}{3}$ 个空地。

又因为在分组中我们把左下角作为了车位，所以还要加上出口的空地。

余下的空地加上分组空地数加上不饱和度再加上出口，最少的空地数为 $1+\frac{n^2-1}{3}+\frac{2(n-1)}{3}-1+1=\frac{n^2-1}{3}+\frac{2(n-1)}{3}+1$。

答案上界即为总面积减空地数 $\frac{2(n^2-1)}{3}-\frac{2(n-1)}{3}$。

空地蛇形分布可以达到这个上界。

证毕。

以下提供三种 $n=10$ 的构造方法：

$n=2023$ 时答案为 $2727004$。