自动搬运

查看原文

来自洛谷，原作者为

	wwxxbb **

搬运于2025-08-24 22:58:25，当前版本为作者最后更新于2024-08-17 11:23:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

省流：此题解是 DLX 学习笔记，会详细地介绍 DLX。

篇幅较长，见谅。

1. 前言

X 算法是由 Donald E. Knuth 提出的，用 Dancing Links 优化，所以叫 DLX。

它用于解决精确覆盖问题和重复覆盖问题。重复覆盖问题还要配合 A* 剪枝。下面讲解精确覆盖问题。

精确覆盖问题的基本模型如下：

给定一个 $n$ 行 $m$ 列的矩阵，矩阵中每个元素要么是 $1$，要么是 $0$。

你需要在矩阵中挑选出若干行，使得对于矩阵的每一列 $j$，在你挑选的这些行中，有且仅有一行的第 $j$ 个元素为 $1$。

这里用 OI wiki 的例子。

假设矩阵为：

$$\begin{pmatrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} $$

普通的搜索复杂度是 $\mathcal{O}(2 ^ n \cdot nm)$ 或 $\mathcal{O}(2 ^ n \cdot m)$ 的，$n, m$ 的范围都不会太大。但是用 DLX 解决 $n, m$ 范围可以达到 $500$ 甚至更大。

2. X 算法

2.1 算法流程

X 算法的流程如下：

1. 选择第一行，将它删除，并将所有 $1$ 所在的列打上标记；

$$\begin{pmatrix} \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 \\ 1 & 0 & \color{Red}0 & 1 & \color{Red}0 & \color{Red}0 & 1 \\ 0 & 1 & \color{Red}1 & 0 & \color{Red}0 & \color{Red}1 & 0 \\ 1 & 0 & \color{Red}0 & 1 & \color{Red}0 & \color{Red}0 & 0 \\ 0 & 1 & \color{Red}0 & 0 & \color{Red}0 & \color{Red}0 & 1 \\ 0 & 0 & \color{Red}0 & 1 & \color{Red}1 & \color{Red}0 & 1 \end{pmatrix} $$

2. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记（重复覆盖问题无需打标记）；

$$\begin{pmatrix} \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 \\ 1 & 0 & \color{Red}0 & 1 & \color{Red}0 & \color{Red}0 & 1 \\ \color{Green}0 & \color{Green}1 & \color{Red}1 & \color{Green}0 & \color{Red}0 & \color{Red}1 & \color{Green}0 \\ 1 & 0 & \color{Red}0 & 1 & \color{Red}0 & \color{Red}0 & 0 \\ 0 & 1 & \color{Red}0 & 0 & \color{Red}0 & \color{Red}0 & 1 \\ \color{Green}0 & \color{Green}0 & \color{Red}0 & \color{Green}1 & \color{Red}1 & \color{Red}0 & \color{Green}1 \end{pmatrix} $$

3. 选择所有被标记的行，将它们删除；

   $$\begin{pmatrix} \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 \\ 1 & 0 & \color{Blue}0 & 1 & \color{Blue}0 & \color{Blue}0 & 1 \\ \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ 1 & 0 & \color{Blue}0 & 1 & \color{Blue}0 & \color{Blue}0 & 0 \\ 0 & 1 & \color{Blue}0 & 0 & \color{Blue}0 & \color{Blue}0 & 1 \\ \color{Blue}0 & \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 \end{pmatrix} $$

   于是得到一个新的小 01 矩阵：

$$\begin{pmatrix} 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{pmatrix} $$

4. 选择第一行（原来的第二行），将它删除，并将所有 $1$ 所在的列打上标记；

$$\begin{pmatrix} \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 \\ \color{Red}1 & 0 & \color{Red}1 & \color{Red}0 \\ \color{Red}0 & 1 & \color{Red}0 & \color{Red}1 \end{pmatrix} $$

5. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记；

   $$\begin{pmatrix} \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 \\ \color{Red}1 & \color{Green}0 & \color{Red}1 & \color{Red}0 \\ \color{Red}0 & \color{Green}1 & \color{Red}0 & \color{Red}1 \end{pmatrix} $$

6. 选择所有被标记的行，将它们删除；

   $$\begin{pmatrix} \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 \\ \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ \color{Blue}0 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 \end{pmatrix} $$

   这样就得到了一个空矩阵。但是上次删除的行 1 0 1 1 不是全 $1$ 的，说明选择有误；

7. 回溯到步骤 4，考虑选择第二行（原来的第四行），将它删除，并将所有 $1$ 所在的列打上标记；

   $$\begin{pmatrix} \color{Red}1 & 0 & \color{Red}1 & 1 \\ \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ \color{Red}0 & 1 & \color{Red}0 & 1 \end{pmatrix} $$

8. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记；

   $$\begin{pmatrix} \color{Red}1 & \color{Green}0 & \color{Red}1 & \color{Green}1 \\ \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ \color{Red}0 & 1 & \color{Red}0 & 1 \end{pmatrix} $$

9. 选择所有被标记的行，将它们删除；

   $$\begin{pmatrix} \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 \\ \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ \color{Blue}0 & 1 & \color{Blue}0 & 1 \end{pmatrix} $$

   于是我们得到了这样的一个矩阵：

   $$\begin{pmatrix} 1 & 1 \end{pmatrix}$$

10. 此时第一行（原来的第五行）有 $2$ 个 $1$，将它们全部删除，得到一个空矩阵，由于上一次删除的时候，删除的是全 $1$ 的行，因此成功。

答案即为被删除的三行：$1, 4, 5$。

2.2 步骤讲解

看起来挺直观的，但为什么是这样的？

首先不考虑无解的情况，我们选了第一行，所以这一行为 $1$ 的列里不能有 $1$，所以把有 $1$ 的列删掉。

列中有 $1$ 的行如果也选的话，就会有多个 $1$ 在同一列，所以要删掉。

这就是一次操作。

我们发现，一次操作已经决定了一些列，这里的决定是指这一列已经有 $1$ 且确定了，于是我们可以对得到的小矩阵进行递归操作继续决定剩下的列。

2.3 无解情况

第 $6$ 步里说上次删的一行不全为 $1$ 所以无解，这又是为什么呢？

这是由于此次操作中这个小矩阵的第二列没有 $1$，不符合题目要求。

所以我们判断无解的情况就是看上一次删除的行是否全为 $1$。

注意，这个删除指的是我们主动选这一行删，而不是在删完这一行后被动地将有 $1$ 的行删掉。

3. Dancing Links

发现 X 算法需要大量的删除和恢复行和列的操作。

我们可以用双向十字链表来优化。

而在双向十字链表上不断跳跃的过程被形象地比喻成「跳跃」，因此被用来优化 X 算法的双向十字链表也被称为「Dancing Links」。

3.1 双向十字链表

双向十字链表中存在四个指针域，分别指向上、下、左、右的元素，且每个元素 $i$ 在整个双向十字链表系中都对应着一个格子，因此还要表示 $i$ 所在的列和所在的行，如图所示：

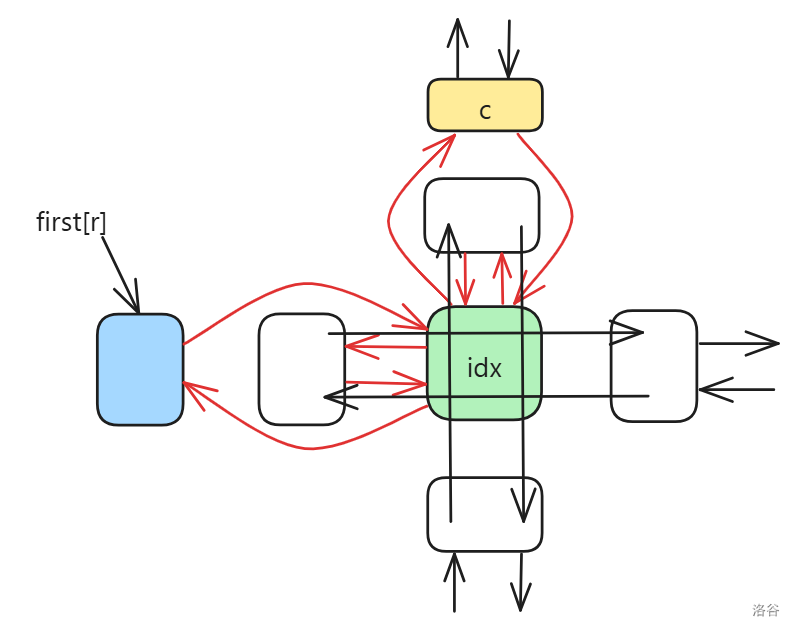
上图就是一个 DLX。DLX 中的元素有 $4$ 中，下面一一介绍。

1. 总表头 (head)

   有且只有一个，作用是方便 DLX 运作。可以通过 DLX 的右节点是否为空判断是否有解。

2. 元素节点 (idx)

   如上图的 $0 \sim 15$，它们表示矩阵中的 $1$。是的，DLX 只需要存 $1$ 就够了。

   一是因为只存 $1$ 方便我们判断；二是因为能用 DLX 解决的问题 $1$ 的数量都比较少，换句话说，这是一个稀疏矩阵，占用内存较少。

3. 行节点 (row) 和列节点 (col)

   它们的作用也是方便 DLX 运作。

我们再将 X 算法的过程用 Dancing Links 模拟一遍：

1. 判断 head.right == head 。如果等于，说明求出解，输出答案并返回 true；否则，继续。
2. 取列元素 p = head.right 。
3. 遍历列元素所在列链，选择一行。
4. 删除与该行链元素冲突的行列，得到一个新的 DLX 。
5. 如果新的 DLX 中仍有列元素且列链为空，则返回 false ；否则跳转步骤 1。
6. 如果选择该行后未求得解，则回溯到当前状态，选择下一行，跳转步骤 5。如果所有行都遍历过仍未求得解，说明之前有行选择错误或无解，返回 false 。
7. 如果最终函数返回值为 false ，则无解。

下面讲一下 DLX 的几个操作。

3.2 变量含义

#define jump(i, p, x) for (int i = p[x]; i != x; i = p[i])
// 用这个宏定义只是为了方便
// 由于我们的链表是循环链表，所以遍历的时候可以一直朝一个方向跳
const int N = 100010; // 我们数组开的大小是 1 的个数 + 列的个数，这里只是一个参考
int n, m, idx;
// n、m 存储 DLX 的大小，下文会讲解如何计算 DLX 大小
// idx 存储的是点的编号
int u[N], d[N], l[N], r[N], first[N];
// u、d、l、r 是每一个点的上、下、左、右点的编号
// first 是每一行第一个元素，方便下面的插入操作
int row[N], col[N], s[N];
// row 和 col 记录的是第 idx 号元素对应在原矩阵的行和列
// s 是每一列的 1 的个数，可以优化 DLX，下面会讲
int ans[N], tot;
// 这是栈，用了存储答案

3.3 创建 (build)

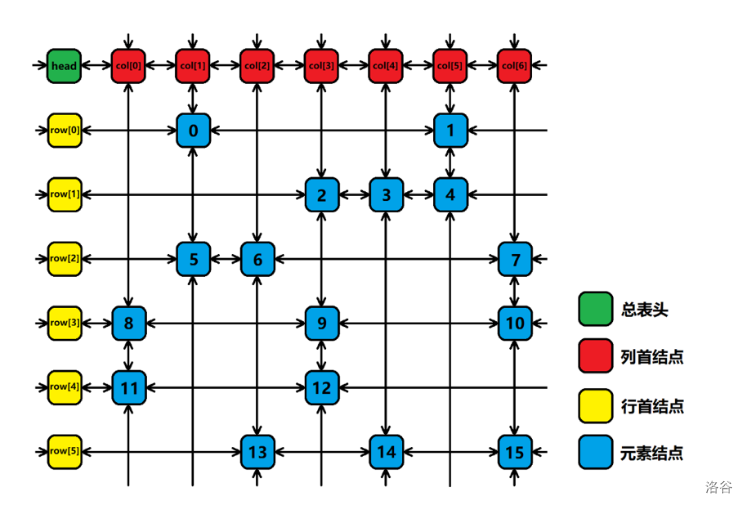
void build(int x, int y) { // 创建一个 x 行 y 列的 DLX
  	n = x, m = y, tot = 0;
	for (int i = 0; i <= m; i ++)
    	u[i] = d[i] = i, l[i] = i - 1, r[i] = i + 1;
    	// 初始的时候 DLX 只有一行，上下节点都是自己，左节点是 i - 1，右节点是 i + 1
  	l[0] = m, r[m] = 0, idx = m + 1; // 0 号点的左边是 m，m 号点的右边是 0，总共有 m + 1 个点
    // 这样可以保证水平、竖直方向上都是循环链表
  	memset(s, 0, sizeof s), memset(first, 0, sizeof first);
}

建完之后的 DLX 长这个样子：

3.4 插入 (add)

void add(int i, int j) { // 在第 i 行 第 j 列插入一个 1
    row[++ idx] = i, col[idx] = j, s[j] ++;
    // idx ++ 表示元素数量加 1，当前元素编号为 idx
    // 记录行和列，这一列的 1 的数量加 1
    u[idx] = j, d[idx] = d[j], u[d[j]] = idx, d[j] = idx;
    if (!first[i]) first[i] = l[idx] = r[idx] = idx;
    else l[idx] = first[i], r[idx] = r[first[i]], l[r[first[i]]] = idx, r[first[i]] = idx;
}

由于链表的插入有些抽象，下面借助图示讲解。

我们先考虑竖直方向。

我们要把 $idx$ 插入到 $c$ 的正下方：

• $idx$ 下方的结点为原来 $c$ 的下结点；
• $idx$ 下方的结点（即原来 $c$ 的下结点）的上结点为 $idx$;
• $idx$ 的上结点为 $c$；
• $c$ 的下结点为 $idx$。

写成代码就是：

u[idx] = j, d[idx] = d[j], u[d[j]] = idx, d[j] = idx; // 这里不建议写连等，可能会挂

变量名有些不一样，见谅。

水平方向要分情况讨论：

• 第 $r$ 行没有元素，即 first[r] = 0，此时这一行的第一个元素就是 $idx$，即 first[r] = idx。由于是循环链表，所以 $idx$ 的左边右边都是 $idx$，写成代码就是：

if (!first[i]) first[i] = l[idx] = r[idx] = idx;

• 第 $r$ 行有元素，我们把 $idx$ 插到 first[r] 的正右方：
  • $idx$ 右侧的结点为原来 first[r] 的右结点；
  • 原来 first[r] 右侧的结点的左结点为 $idx$；
  • $idx$ 的左结点为 first[r]；
  • first[r] 的右结点为 $idx$。

else l[idx] = first[i], r[idx] = r[first[i]], l[r[first[i]]] = idx, r[first[i]] = idx;
// 这里的 else 和上面的 if 是匹配的

合起来就是上面的代码。

3.5 递归 (dance)

函数 dance 的类型是 bool，因为要判无解。

下面代码先抛出两个操作：

• 删除 (delete)
• 撤销 (undo)

用于删除一列和恢复一列。

bool dance() {
    if (!r[0]) return 1;
    // 如果 0 号结点没有右结点，那么矩阵为空，则有解
    // 这就是总表头 0 号点的作用
    int p = r[0];
    jump(i, r, 0) if (s[i] < s[p])
        p = i;
    // 这就是上面说到的优化，每次删去 1 个数最少的一列，类似高斯消元，这样能保证程序具有一定的启发性，使搜索树分支最少
    del(p); // 把这一列删掉
    jump(i, d, p) { // 遍历删除的那一列
        ans[++ tot] = row[i]; // 记录当前删去的行
        jump(j, r, i) del(col[j]); // 删去当前列有 1 的行
        // 我们删除行的时候是遍历这一行的所有列，再把这一列删掉
        // 这就是 DLX 里面只存 1 的好处，不需要任何判断，直接删就完了
        if (dance()) return 1; // 递归下一层，如果有解，就返回 true
        jump(j, l, i) undo(col[j]); // 恢复这一行
        // 重点！！！我们在恢复的时候，怎么删的，就要怎么反过来恢复，操作的顺序也要反过来，在两个函数里面也是一样的
        // 如果不反过来，在一些题目会死循环，下面有原因
        tot --; // 回溯
    }
    // 如果程序运行到这里，就说明当前删的这行会导致无解，所以返回 false 并恢复这一列
    undo(p);
    return 0;
}

3.5.1 关于恢复操作的方向的问题

结论：恢复的顺序要与删除的顺序相反，操作的顺序也要相反。

这由删除函数和恢复函数的性质决定，注意删除列 $c$ 时，$c$ 列中的 u 和 d 都没有更改，这样做的目的是方便恢复。所以在接下来的操作中，$c$ 列中的 u 和 d 也不能变。

考虑依次删除的列 $c_1$，$c_2$，且它们包含同一行，那么删 $c_2$ 时，$c_1$ 的 u，d 就变了！所以在恢复时应先恢复 $c_2$ 再恢复 $c_1$，否则链表指针会错乱，引起死循环。

3.6 删除 (delete)

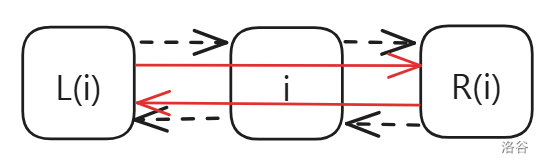
delete(p) 表示在 DLX 中删除第 $p$ 列以及与其相关的行和列。

void del(int p) {
    r[l[p]] = r[p], l[r[p]] = l[p];
    /* 这里同样是对链表进行操作，可以这样理解：
     p 左侧的结点的右结点应为 p 的右结点
     p 右侧的结点的左结点应为 p 的左结点
    */
    jump(i, d, p) // 顺着这一列往下走，把走过的每一行都删掉
        jump(j, r, i) { // 遍历当前行的每一列
        u[d[j]] = u[j], d[u[j]] = d[j];
        /*
        j 上方的结点的下结点应为 j 的下结点。
		j 下方的结点的上结点应为 j 的上结点。
        */
        s[col[j]] --;
        // 每一列的元素个数要减 1
    }
}

配上图片理解：

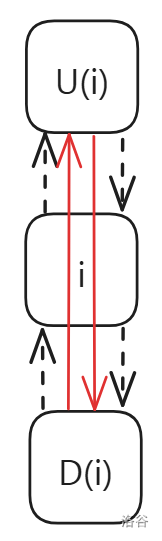
3.7 撤销 (undo)

undo(p) 表示在 DLX 中还原第 $p$ 列以及与其相关的行和列。

注意操作顺序要与删除时相反，原因上面讲过。

void undo(int p) {
    jump(i, u, p) // 注意这里
        jump(j, l, i) { // 注意这里
        d[u[j]] = u[d[j]] = j;
        s[col[j]] ++;
    }
    r[l[p]] = l[r[p]] = p; // 还有这里
}

模板题代码：

#include <bits/stdc++.h>
using namespace std;

struct DLX {
    #define jump(i, p, x) for (int i = p[x]; i != x; i = p[i])
    static const int N = 5000 + 500 + 10;
    // 上面讲过，数组大小是 1 的个数 + 列的个数
    // 在模版题里，1 的个数是 5000，列有 500，加了 10 是为了防止越界
    // 其实不用那么精打细算，多开一点更保险

    int n, m, idx;
    int u[N], d[N], l[N], r[N], first[N];
    int s[N], row[N], col[N];
    int ans[N], tot;
    
    void build() {
        tot = 0;
        for (int i = 0; i <= m; i ++)
            u[i] = d[i] = i, l[i] = i - 1, r[i] = i + 1;
        l[0] = m, r[m] = 0, idx = m + 1;
        memset(s, 0, sizeof s), memset(first, 0, sizeof first);
    }

    void add(int i, int j) {
        row[++ idx] = i, col[idx] = j, s[j] ++;
        u[idx] = j, d[idx] = d[j], u[d[j]] = idx, d[j] = idx;
        if (!first[i]) first[i] = l[idx] = r[idx] = idx;
        else l[idx] = first[i], r[idx] = r[first[i]], l[r[first[i]]] = idx, r[first[i]] = idx;
    }

    void del(int p) {
        l[r[p]] = l[p], r[l[p]] = r[p];
        jump(i, d, p)
            jump(j, r, i) {
                s[col[j]] --;
                u[d[j]] = u[j], d[u[j]] = d[j];
            }
    }

    void undo(int p) {
        jump(i, u, p)
            jump(j, l, i) {
                d[u[j]] = u[d[j]] = j;
                s[col[j]] ++;
            }
        r[l[p]] = l[r[p]] = p;
    }
    
    bool dance() {
        if (!r[0]) return 1;
        int p = r[0];
        jump(i, r, 0) if (s[i] < s[p])
            p = i;
        del(p);
        jump(i, d, p) {
            ans[++ tot] = row[i];
            jump(j, r, i) del(col[j]);
            if (dance()) return 1;
            jump(j, l, i) undo(col[j]);
            tot --;
        }
        undo(p);
        return 0;
    }
} X;

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> X.n >> X.m;
    X.build();
    for (int i = 1; i <= X.n; i ++)
        for (int j = 1, x; j <= X.m; j ++) {
            cin >> x;
            if (x) X.add(i, j);
        }
    if (X.dance()) for (int i = 1; i <= X.tot; i ++)
        cout << X.ans[i] << ' ';
    else cout << "No Solution!";
    return 0;
}

封装了 DLX 模版，需要自取。

4. 建模

DLX 的难点，不全在于链表的建立，而在于建模。

请确保已经完全掌握 DLX 模板后再继续阅读下文。

我们每拿到一个题，应该考虑行和列所表示的意义：

• 行表示 决策，因为每行对应着一个集合，也就对应着选或不选；
• 列表示 状态，因为每一列对应着某个条件。

对于某一行而言，由于不同的列的值不相同，我们 由不同的状态，定义了一个决策。

5. 例题

P1784 数独。

思路

行代表问题的所有情况，列代表问题的约束条件。每个格子能够填的数字为 $[1, 9]$，并且总共有 $9 \times 9$ 个格子，所以总的情况数为 $729$ 种。也就是 DLX 有 $729$ 行。列则分为四种：

1. $[1, 81]$ 列分别对应了 $9$ 行，每行共 $9$ 个数字的放置情况；
2. $[82, 162]$ 列分别对应了 $9$ 列，每列共 $9$ 个数字的放置情况；
3. $[163, 243]$ 列分别对应了 $9$ 个宫，每个宫共 $9$ 个数字的放置情况；
4. $[244, 324)$ 列 分别对应了 $81$ 个格子是否被放置了数字。

所以总的列数为 $4 \times 81 = 324$ 列。

即我们建立的 DLX 大小为 $729 \times 324$，$1$ 的个数为 $729 \times 4 = 2916$ 个。

注意：搜索题比较玄学，有些时候 TLE 了可以改变不同范围内决策的顺序，比如说，我们可以让 $[1, 81]$ 列决定宫，$[163, 243]$ 列决定行。

参考代码：

#include <bits/stdc++.h>
using namespace std;

int res[10][10]; // 存储输入和答案

struct DLX {
    #define jump(i, p, x) for (int i = p[x]; i ^ x; i = p[i])
    static const int N = 9 * 9 * 9 * 4 + 9 * 9 * 4 + 10;
    // 这里数组开 2916 + 324。我多开了个 10

    int n, m, idx;
    int u[N], d[N], l[N], r[N], first[N];
    int s[N], row[N], col[N];
    int ans[N], tot;
    
    void build(int x, int y) {
        n = x, m = y;
        for (int i = 0; i <= m; i ++)
            u[i] = d[i] = i, l[i] = i - 1, r[i] = i + 1;
        l[0] = m, r[m] = 0, idx = m + 1;
    }

    void add(int i, int j) {
        row[++ idx] = i, col[idx] = j, s[j] ++;
        u[idx] = j, d[idx] = d[j], d[j] = u[d[j]] = idx;
        if (!first[i]) first[i] = l[idx] = r[idx] = idx;
        else l[idx] = first[i], r[idx] = r[first[i]], l[r[first[i]]] = idx, r[first[i]] = idx;
    }

    void del(int p) {
        l[r[p]] = l[p], r[l[p]] = r[p];
        jump(i, d, p)
            jump(j, r, i) {
                s[col[j]] --;
                u[d[j]] = u[j], d[u[j]] = d[j];
            }
    }

    void undo(int p) {
        jump(i, u, p)
            jump(j, l, i) {
                d[u[j]] = u[d[j]] = j;
                s[col[j]] ++;
            }
        r[l[p]] = l[r[p]] = p;
    }
    
    bool dance() {
        if (!r[0]) {
            for (int i = 1; i <= tot; i ++) {
                int x = (ans[i] - 1) / 81 + 1;
                int y = (ans[i] - 1) / 9 % 9 + 1;
                int v = (ans[i] - 1) % 9 + 1;
                res[x][y] = v; // 这里是根据行号利用公式决定行、列和数字
            }
            return 1;
        }
        int p = r[0];
        jump(i, r, 0) if (s[i] < s[p])
            p = i;
        del(p);
        jump(i, d, p) {
            ans[++ tot] = row[i];
            jump(j, r, i) del(col[j]);
            if (dance()) return 1;
            jump(j, l, i) undo(col[j]);
            tot --;
        }
        undo(p);
        return 0;
    }
} X;

void insert(int r, int c, int x) { // 在第 r 行第 c 列放置 x 数字
    int id = (r - 1) * 81 + (c - 1) * 9 + x; // 计算行号
    int n1 = (r - 1) * 9 + x; // 行
    int n2 = (c - 1) * 9 + x + 81; // 列
    int n3 = ((r - 1) / 3 * 3 + (c - 1) / 3) * 9 + x + 162; // 宫
    int n4 = (r - 1) * 9 + c + 243; // 格子
    // 公式可以自己去推
    X.add(id, n1);
    X.add(id, n2);
    X.add(id, n3);
    X.add(id, n4);
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    X.build(729, 324);
    for (int i = 1; i <= 9; i ++) {
        for (int j = 1; j <= 9; j ++) {
            cin >> res[i][j];
            if (res[i][j]) insert(i, j, res[i][j]); // 如果不为 0，则只有 1 种决策
            else for (int k = 1; k <= 9; k ++) insert(i, j, k); // 否则有 9 种决策
        }
    }
    X.dance();
    for (int i = 1; i <= 9; i ++, cout << '\n')
        for (int j = 1; j <= 9; j ++)
            cout << res[i][j] << ' ';
    return 0;
}

多倍经验：

• P1074 靶形数独

• P10481 Sudoku

• P10482 Sudoku 2

• SP1110 Sudoku

• UVA1309 Sudoku

其中 P1074 要加权值；P10482 多测记得清空清干净；SP1110 和 UVA1309 数独边长为 $16$，将与 $9$ 有关的改成 $16$ 即可。

要代码的可以私信我。

参考资料

• OI wiki
• 个人理解