自动搬运

查看原文

来自洛谷，原作者为

	LionBlaze @wsx 我这么弱你还说我批话/ll || 有实力或没那么有实力的欢迎加入 WROI /team/96917 || 前置声明：不当除了 WROI 之外任何公开赛的背锅人。接受私信协商。

搬运于2025-08-24 22:58:18，当前版本为作者最后更新于2024-05-18 13:49:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

总：本文中介绍了方法一和方法二，方法一可能偏难，方法二偏简单（本人主观判断），方法一实现 $184$ 行，方法二 $134$ 行（没有压行，不删注释，不删空行）。

方法 $1$（2024/5/18）

如何进行表达式计算？

我们通常使用的表达式，比如 $(2+2)^{(1+1)}$、$1+1$、$11 \times 11 - 11 + 11 \div 11^{(11 - 11) + (11 \div 11)} $，都叫做中缀表达式，意思是符号在两个运算符中间。

中缀表达式虽然好理解（对于人类），但是对于计算机不好计算。具体为什么，可以试一试，不是完全不可以但是特别难写（比如优先级）。

既然有中缀表达式，那肯定还有：

• 前缀表达式：符号在数字的前面。比如中缀表达式 (2+2)^(1+1) 的前缀表达式就是 ^ + 2 2 + 1 1。这种表达式便于程序求值，也绝对不会有括号，但是把中缀表达式变为前缀表达式比较困难。
• 后缀表达式：符号在数字的后面。比如中缀表达式 (2+2)^(1+1) 的后缀表达式就是 2 2 + 1 1 + ^。这种表达式既便于程序求值，也不会有括号，从中缀转成后缀也不难。所以我们就选用后缀表达式进行计算。

中缀表达式转后缀表达式

首先，中缀表达式转后缀表达式，具体流程：

1. 定义一个运算符栈。
2. 如果是数字，直接加入后缀表达式。
3. 如果是字符，按以下流程处理：
4. 如果为 (，直接压栈。
5. 若为 )，依次弹出栈顶元素加入后缀表达式，直到遇到 (，停止，然后将 ( 出栈。
6. 如果比栈顶运算符的优先级高，或者栈顶元素为 (，或者栈为空，直接压栈。
7. 否则，依次弹出栈顶元素加入后缀表达式，直到遇到比它优先级低的元素，或者遇到 (。
8. 如果最后还剩下，直接依次出栈加入后缀表达式。

update:这里有个细节问题没讲到，由于 ^ 乘方运算是从右往左计算的，所以在第 $7$ 步，如果是乘方运算，就要把“优先级低”改成“优先级低或相等”。

以样例为例：

(2+2)^(1+1)

字符或数字	操作	栈（左底右顶）	后缀表达式
(	直接入栈	(	（空）
$2$	直接加入后缀表达式		2
+	此时栈顶元素为 (，压栈	( +
$2$	直接加入后缀表达式		2 2
)	依次出栈直到 (，最后将 ( 出栈	（空）	2 2 +
^	此时栈为空，直接入栈	^
(	直接入栈	^ (
$1$	直接加入后缀表达式		2 2 + 1
+	此时栈顶元素为 (，压栈	^ ( +
$1$	直接加入后缀表达式		2 2 + 1 1
)	依次出栈直到 (，最后将 ( 出栈	^	2 2 + 1 1 +
（EOF）	此时栈未空，依次出栈	（空）	2 2 + 1 1 + ^

细节：

判断 +、- 是正负号还是加减号。如果左边是数字或右括号，就是加减号。否则就是正负号。

计算

计算流程：

1. 定义一个数字栈。
2. 如果是数字，直接压栈。
3. 如果是运算符，取两个栈顶元素，将运算结果重新压栈。

最后栈中剩下的就是结果。

以样例为例（后缀表达式我们刚才一起求了，2 2 + 1 1 + ^）：

字符或数字	操作	栈（左底右顶）
$2$	入栈	$2$
		$2,2$
+	取出两个栈顶元素，相加后放回去	$4$
$1$	入栈	$4,1$
		$4,1,1$
+	取出两个栈顶元素，相加后放回去	$4,2$
^	取出两个栈顶元素，进行乘方操作后后放回去	$16$
（EOF）	最后剩下 $16$，答案为 $16$

细节：因为栈是先进先出，所以取出的时候也会反过来，比如（左底右顶）栈为 1 2，伪代码：

a ← top; //将a赋值为栈顶
pop(); //出栈
b ← top; //将b赋值为栈顶
pop(); //出栈

得到的结果是 a = 2, b = 1，此时如果要进行不满足交换律的运算（-、/ 和 ^），直接计算 a -,/,^ b 就会导致错误（比如减法，应为 $-1$ 计算为 $1$）。有两种方法，一是先赋值 b，再赋值 a，另一种是计算时颠倒顺序，总之就是要颠倒顺序。

时间复杂度

线性，但不知道如何证明。主要纠结与快速幂复杂度。

附：帮助

我这题提交了 $28$ 次才过，自认为坑已经踩得很全面了。

如果你 $20$ 分，像这样：RE+RE+AC+WA+WA，可能是两个错误：一是没判断多余括号，二是正负号判断错误。你的正负号可能是这样判断的：左右两边都是数字。

如果你 $40$ 分，像这样：RE+RE+AC+AC+WA，可能是两个错误：一是没判断多余括号，二是正负号判断错误。你的正负号可能是这样判断的：左边是数字。

如果你 $80$ 分，像这样：AC+AC+AC+AC+WA，可能是正负号判断错误，错误同上。

如果你 $100$ 分，像这样：AC+AC+AC+AC+AC，那么恭喜，因为这道题截止到现在一共还只有 $25$ 人通过。

方法 $2$（2024/7/15）

表达式树

顾名思义，肯定是一棵树，代表一个表达式，每个节点要么是数字，要么是运算符。

对于每个节点：

• 数字节点：没有儿子。
• 运算符节点：这种运算有几个操作数就有几个儿子，代表这个运算的所有操作数（或式）。

而对于这道题，所有的运算都有且只有两个操作数，所以是一颗二叉树。

比如中缀表达式 (2+2)^(1+1) 转换成表达式树是这样的：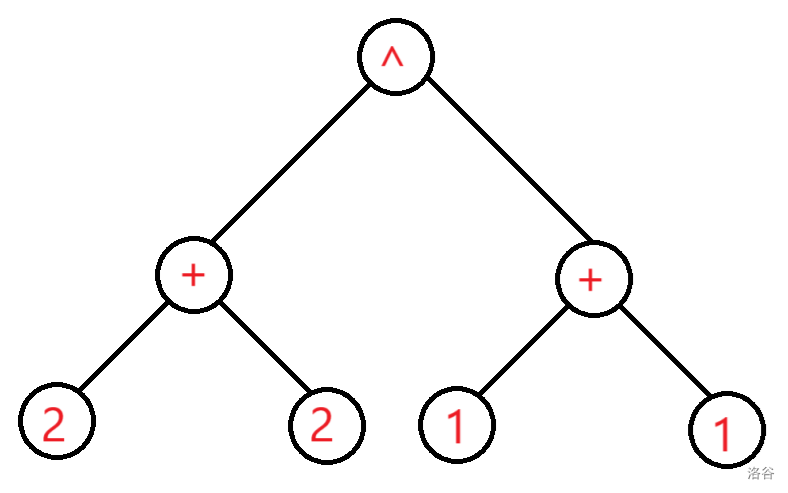

比如根节点 ^，左子树是 2 + 2，右子树是 1 + 1，分别是两个操作数。

再比如根节点的左子结点 +，左子树和右子树都是 2，也分别是两个操作数。

易知，每个表达式都对应一个表达式树。

表达式树和前/中/后缀表达式的联系

回顾：

前缀表达式是：符号在前。

中缀表达式是：符号在中间。

后缀表达式是：符号在后。

如果我们换一种方法表达呢？

前缀表达式是：符号 $\to$ 操作数 $1 \to$ 操作数 $2$。

中缀表达式是：操作数 $1 \to$ 符号 $\to$ 操作数 $2$。

后缀表达式是：操作数 $1 \to$ 操作数 $2 \to$ 符号。

二叉树的三种遍历：

前序遍历：根节点 $\to$ 左子结点 $\to$ 右子节点。

中序遍历：左子结点 $\to$ 根节点 $\to$ 右子节点。

后序遍历：左子结点 $\to$ 右子节点 $\to$ 根节点。

是不是感觉一模一样？

所以，表达式树的前序遍历就是前缀表达式，中序遍历就是中序表达式，后序遍历就是后续表达式，但是注意中序遍历（中缀表达式）要适当加括号。

中缀表达式转表达式树

1. 找到最后计算的运算，以及它的两个操作数。
2. 将它的两个操作数分别当做左子树和右子树，递归计算。

没了，只有细节：

如何找到最后计算的运算？

首先，如果整个表达式都被括号套着，把括号（可能是多层）去掉。

然后扫三边，扫的时候直接忽略括号中的内容。

第一遍找 +,-，从右往左，如果找到了就是最后计算的运算。

第二遍找 *,/，从右往左，如果找到了就是最后计算的运算。

第三遍找 ^，从左往右，如果找到了就是最后计算的运算。

如果三遍都没找到，说明：

1. 所有都被括号套着 - 前面已经处理过，不可能的。
2. 括号外都没有运算符 - 说明全是数字，结果就是数字。

注意一个点，判断是否整个表达式被括号套着，不能只判断是否开头是 ( 且结尾是 )，样例就可以 hack，需要使用类似这道题的方法，扫一遍，扫的时候括号嵌套层数的最小值就是整个表达式被套了多少层。

如何找到最后计算的运算左右两边的操作数？

既然是最后计算的运算，左边必定是左操作数，右边必定是右操作数。

如何计算

实在没什么好讲的。递归即可。

时间复杂度

线性，但是如果你在建树的时候直接使用 string::substr，会导致时间复杂度变为平方级别，可以维护两个变量，分别是当前字串的左右边界下标。但是我在实现中使用的是平方级别的。（虽然但是，最大长度为 $30$ 的话……）

处理多余括号

题目中说还有可能出现多余括号情况，感觉不太好处理。但是其实可以这样做：

多了左括号和右括号，既然左右是配对的，所以多左括号相当于少右括号，多右括号相当于少左括号。如果少了某种括号，那么在算式的最左边或最右边添加就好了。

给出伪代码：

bracnt ← 0 //当前括号的嵌套个数
for ch in input: //对于输入中每一个字符，从左到右遍历
	if(ch == '('): //如果是左括号
		bracnt++; //说明括号嵌套深了一层
   if(ch == ')'): //如果是右括号
		bracnt--; //说明括号嵌套少了一层
if(bracnt < 0): //括号嵌套 < 0，说明右括号多，也就是缺少左括号
	input = '(' * (-bracnt) + input; //缺少左括号，在左边加上。
if(bracnt > 0): //括号嵌套 > 0，说明左括号多，也就是缺少右括号
	input = input + ')' * bracnt; //缺少右括号，在左边加上。

$$\color{red}{\text{注意！这样做是错误的！}}$$

给出 hack 数据：

)1+1(

最后，左括号和右括号数量相等，但是括号仍然不匹配！所以应该过程中就判断（最后仍然要判断一遍）。

完结撒花！我好像把另一个我忘了叫什么的题也讲了。

代码

为了不使题解太长，两个方法的代码放在云剪贴板里：click me。

另：码了这么多次，如有错误（比如错别字）请指出！