自动搬运

查看原文

来自洛谷，原作者为

	Atserckcn 愿你的刀仍然锋利

搬运于2025-08-24 22:58:01，当前版本为作者最后更新于2024-05-16 17:32:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P10447 最短 Hamilton 路径 题解

分析题目：

一张 $n$ 个点的带权无向图，求起点 $0$ 至终点 $n-1$ 的最短 Hamilton 路径（从 $0\sim n-1$ 不重复地经过每个点一次）。

初看题目，不难发现这道题是一个状态压缩 dp 的模板题。

状态压缩简介：

状态压缩，字面意思就是把复杂的状态转化成简洁的二进制来表示，可减少时间与空间复杂度。

打个比方，二进制数 $01001101$ 表示的意思为：

$0$（$0$ 号节点没有被经过）$1$（$1$ 号节点已被经过）$00$（$2,3$ 号节点未经过）$11$（$4,5$ 号节点经过）$0$（$6$ 号节点没经过）$1$（$7$ 号节点已经过）。

而 $(01001101)_2=(77)_{10}$，我们只需操作 $77$ 次即可，简洁明了。

分析题目样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

可作图如下：

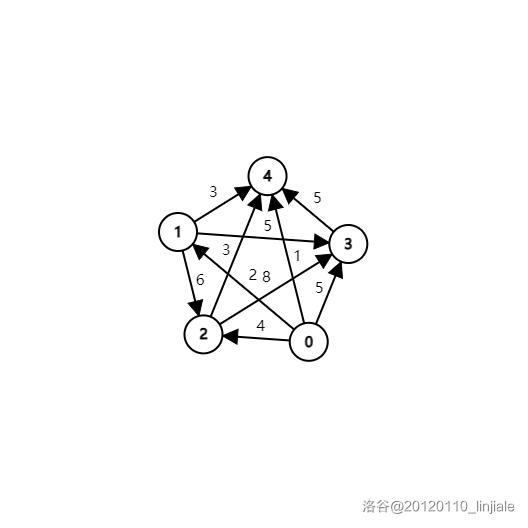
好啦，分析题目，我们不难想出定义一个 $f$ 数组，$f_{i,j}$ 表示在 $i$ 的状态下（上文已提到）最后经过的节点 $j$ 所得的最短 Hamilton 路径。

定义：

int f[MAXM][MAXN];

那么我们该如何进行状态转移呢？

我们可以用三层循环来实现：

for(int i=1;i<(1<<n);i++)//枚举状态
	{
		for(int j=0;j<n;j++)//枚举每个点
		{
			if(!((i>>j)&1)) continue;//如果点j已经被经历过，就跳过它
			for(int k=0;k<n;k++)//这里比较难想，意思是在i的状态下已被经过的点的个数
				if(((i^(1<<j))>>k)&1)
					f[i][j]=min(f[i][j],f[i^(1<<j)][k]+a[k][j]);//状态转移方程，要么是本身，要么则为以i^(1<<j)为状态的节点k到j，有点类似最短路的floyd
		}
	}

最后我们的答案就是 $f_{2^{n}-1 , n-1}$。

即在状态为 $2^{n}-1$（全被经过了）下的 $n-1$ 号节点。

AC Code:

#include<bits/stdc++.h>
using namespace std;
const int MAXN=25,MAXM=(1<<20),inf=0x3f;//定义变量，inf为无限
int n,a[MAXN][MAXN],f[MAXM][MAXN];
int main(){
	scanf("%d",&n);
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			scanf("%d",&a[i][j]);
   	//输入无需多嘴
	memset(f,inf,sizeof(f));//一开始f数组都是无限的
	f[1][0]=0;//还没开始旅程，为0
	for(int i=1;i<(1<<n);i++)//枚举状态
	{
		for(int j=0;j<n;j++)//枚举每个点
		{
			if(!((i>>j)&1)) continue;//经过了
			for(int k=0;k<n;k++)//上一次经过了哪些点？
				if(((i^(1<<j))>>k)&1)//枚举从上一个经过的节点走到j节点
					f[i][j]=min(f[i][j],f[i^(1<<j)][k]+a[k][j]);//状态转移
		}
	}
	printf("%d\n",f[(1<<n)-1][n-1]);//out
	return 0;
    //完结撒花
}

AC 记录