1 条题解
-
0
自动搬运
来自洛谷,原作者为

suzy0921
弱爆了的菜鸡很困搬运于
2025-08-24 22:57:52,当前版本为作者最后更新于2024-08-14 19:23:29,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题目分析
看到那么大长串的柿子不要慌
$$\begin{aligned} S &= H _ {a} H _ {b} H _ {c} \cdot \frac{\operatorname{LCM}(H _ {a}, H _ {b}, H _ {c})}{\operatorname{LCM}(H _ {a}, H _ {b}) \cdot\operatorname{LCM}(H _ {a}, H _ {c}) \operatorname{LCM}(H _ {b}, H _ {c})}\\ &= (d \times h \times j \times g) \times (g \times j \times e \times i) \times (j \times i \times h \times f) \times\frac{(d \times e \times f \times g \times h \times i \times j)}{(d \times g \times h \times j \times i \times f) \times (d \times g \times h \times j \times e \times i) \times (h \times j \times i \times f \times g \times e)} \end{aligned}\\ $$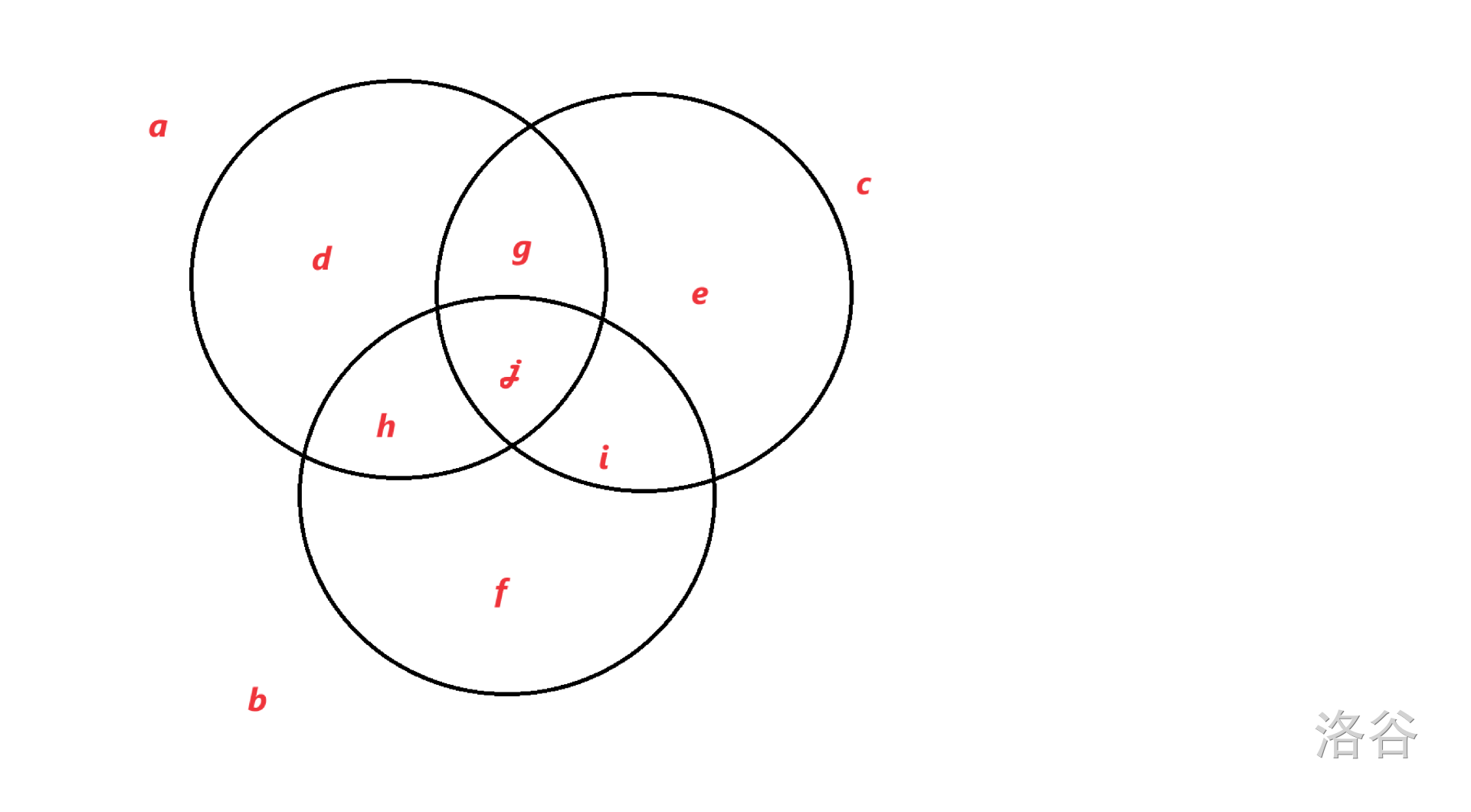 我们把式子 看作圈 ,把式子 看作圈 ,把式子 看作圈
我们把式子 看作圈 ,把式子 看作圈 ,把式子 看作圈 化简完之后我们得到了
指的是 ,所以
做题思路
1.找一个 用于记录从 一直到 中能被 整除的个数。
2.找到最大的 使得 记为
3.从小到大排序 数组。
4.从 到 遍历,判断 ,输出前 3 个满足要求的数。代码
#include<bits/stdc++.h> using namespace std; const int N=1e5+5; int h[N],cnt[N]; int main() { int n,x,c=0; cin>>n; for(int i=1;i<=n;i++){ cin>>h[i]; for(int j=1;j*j<=h[i];j++) { if(h[i]%j==0){ cnt[j]++; if(j*j!=h[i]) cnt[h[i]/j]++; } } } for(int i=N-5;i>=1;i--){ if(cnt[i]>=3){ x=i; break; } } sort(h+1,h+n+1); for(int i=1;i<=n;i++){ if(h[i]%x==0){ cout<<h[i]<<" "; c++; } if(c==3) return 0; } return 0; }完结撒花
点个赞趴
- 1
信息
- ID
- 10227
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 3
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
